Альтернативные сетевые модели
PERT-анализ даёт упрощённую оценку ситуации, описываемой математической моделью. Чаще всего различные оценки продолжительности работ подразумевают под собой проблемы использования каких-либо ресурсов (например, смена исполнителя, задержки в поставках). Для более детального анализа проекта применяются вероятностные сети, в которых структура не является детерминированной – это альтернативные сети (в соответствии с принятой ранее классификацией). Благодаря введению вероятностных типов событий со взаимосвязями типа «и», «или», «исключающее или» вероятностные модели дают более мощный инструмент для управления реальными проектами.
По сравнению с сетями с детерминированной структурой, в альтернативных сетях расширено понятие «событие». Каждый внутренний узел сети (в представлении «узел – событие») «выполняет входную и выходную функцию» [21], при этом для начального события существует только выходная функция, а для конечного – только входная.
Существует три типа входных функций, которые представлены в Таблица 1.9.
Таблица 1.9.
| Типы входных функций узла. | |||
| Тип | Описание входной функции | Логическая характеристика | Графическое обозначение |
| Узел выполняется, если выполнены все дуги, входящие в него | «И» |  | |
| Узел выполняется, если выполнена любая из дуг, входящих в него | «ИЛИ» |  | |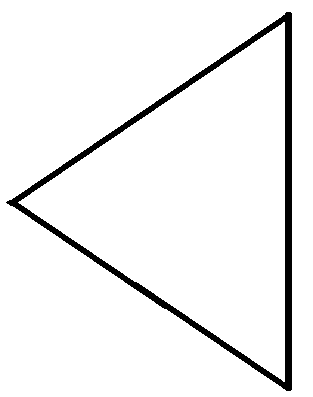
| Узел выполняется, если в данный момент выполнена одна и только одна из дуг, входящих в него | Исключающее« ИЛИ» |  |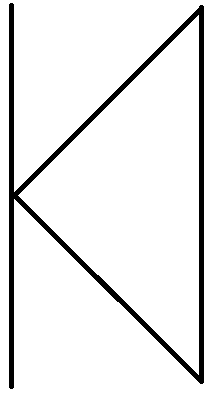
Два типа выходных функций представлены в таблице 1.10.
Таблица 1.10.
| Типы выходных функций узла. | |||
| Тип | Описание выходной функции | Логическая характеристика | Графическое обозначение |
| Выполняются все дуги, выходящие из узла | «И» |  | |
| Из всех выходящих дуг выполняется только одна | «ИЛИ» |  |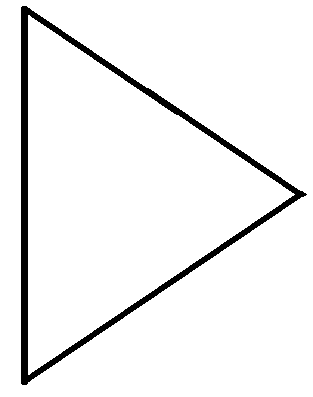
Дуга в данной модели описывает любую функциональную зависимость между узлами, в том числе и работы. Каждая дуга, обозначающая работу, имеет две характеристики: продолжительность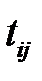 
и вероятность того, что эта работа будет выбрана среди других 
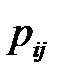при условии, что реализуется узел (событие) i, из которого исходит эта дуга.
Для стохастических сетей характерно наличие обратной связи и петель (например, при контроле качества), то есть события могут наступать более одного раза.
Сетевые модели с описанными свойствами используются в методе графической оценки и анализа GERT. Основные этапы применения данной методики таковы:
- создание сетевой модели на основе качественного описания системы (проблемы);
- сбор данных, необходимых для описания каждой дуги сети;
- получение эквивалентной функции из одной дуги между двумя узлами сети;
- преобразование полученной функции в следующие показатели эффективности сети;
- вероятность реализации каждого узла;
- функция времени в замещающей сети;
- оценка полученных в предыдущих пунктах результатов.
- Для этапов 3 и 4 можно привести обобщение на всю модель:
- минимизация построенной сети;
- приведение сети к виду, когда возможно определить продолжительности и вероятности реализации проекта и расчёт этих параметров.
В GERT-анализе для описания стохастической сети достаточно использовать два типа узлов: с третьим типом входной функции и первым типом выходной, и с третьим типом входной функции и вторым типом выходной (Табл. 1.9 – 1.10). При этом допускается использование первого типа входной функции, если в вершину входит лишь одна дуга. Обоснование данного ограничения приведено в [24].
Для записи символы входной и выходной функции соединяют как указано в
Таблица 1.11.
Таблица 1.11.
| Обозначения узлов, используемых в GERT–сетях. | |||||
| Графическое изображение |  |  |  |  | |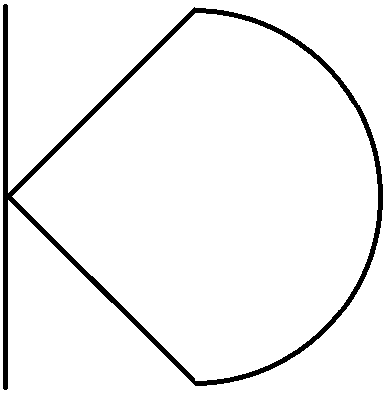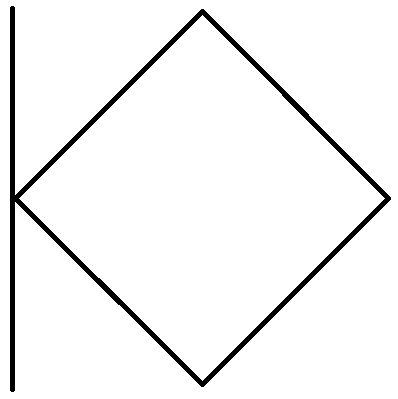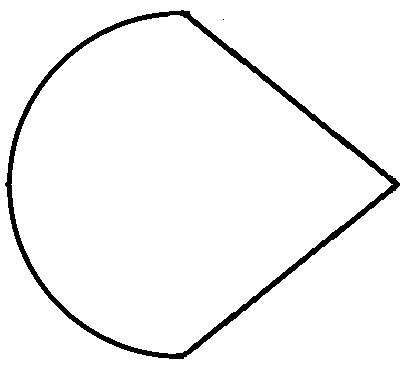
| Тип входной – выходной функции | 3–1 | 3–2 | 1–2 | 1–1 | |
Рассмотрим базисные преобразования для оптимизации сети. Участок сети из двух последовательных дуг (
Рис. 1.9) можно заменить одной.
Рис. 1.9. Последовательные узлы.
Для новой сети временные параметры вычисляются следующим образом:
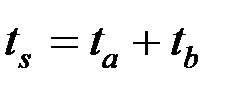 , | (1.26) |
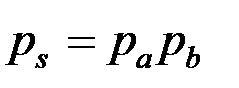 . | (1.27) |
Две дуги между двумя узлами, второй из которых входной функцией имеет «исключающее или» (
Рис. 1.10), можно заменить на эквивалентную дугу со следующими параметрами.
Рис. 1.10. Параллельные дуги.
Формулы расчета параметров:
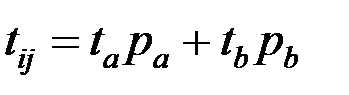 , | (1.28) |
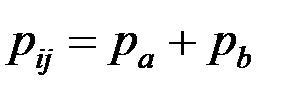 . | (1.29) |
Если же вторая дуга имеет входную функцию «ИЛИ», то время для эквивалентной дуги будет вычисляться иначе:
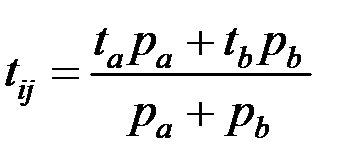 , | (1.30) |
Формулы для параллельных дуг также возможно обобщить для случая большего количества.
Рис. 1.11. Петля.
Петлю (рис. 1.11) можно удалить, учитывая, что количество исходящих из узла дуг сократится, следовательно, необходим пересчёт вероятности. Соответствующие формулы для времени и вероятности представлены ниже.
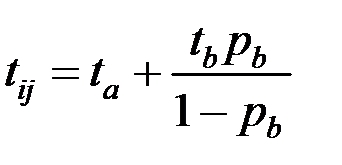 , | (1.31) |
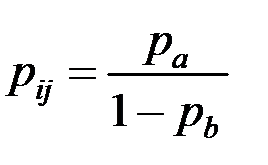 . | (1.32) |
Очевидно, что при отсутствии альтернативных дуг, исходящих из узла i,вероятность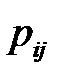 
будет равна 1. Применяя правила сокращения последовательных дуг и петли, можно сокращать и контуры (замкнутые пути в графе). Комбинации этих преобразований позволяют упростить сеть до одной дуги. Таким образом, длительность дуги окажется длительностью проекта, а вероятность этой дуги ( 
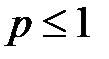) – вероятность выполнения проекта. Для определённых задача возможно упрощение до модели с несколькими узлами, если суть итогов разнится, и необходимо узнать вероятность и время наступления каждого из них.
Практическое использование того или иного типа модели зависит от многих причин, связанных как с подготовленностью руководителей и исполнителей проекта, так и с объективными особенностями и ограничениями.
Применение детерминированной сетевой модели и МКП позволяет узнать лишь продолжительность проекта, критические работы и последовательность выполнения операций. Он нагляден, если в качестве узлов брать ключевые этапы проекта, то есть рассматривать второй-третий уровень иерархии СРР. Однако для проекта в тысячи операций этот метод даёт мало информации.
Метод PERT более гибкий, так как включает в себя оценки, получаемые из статистических данных, что приближает сетевую модель к реальности. Однако результаты PERT-анализа являются смещёнными, тогда как GERT-моделирование приводит к несмещённым оценкам [25].
Что касается альтернативных моделей, то в настоящее время разрабатывается как математический аппарат, основанный на теории и/или графов, так и программное обеспечение, но практическая применимость его пока недоступна.
Выводы
Приведенный обзор методов сетевого планирования и управления свидетельствует о широких возможностях их применения для различных классов задач, в том числе и для проектного управления. Выделены три основных типа сетевых моделей: детерминированные сетевые модели (ДСМ), вероятностные сетевые модели (ВСМ), альтернативные сетевые модели (АСМ). Приведены методы расчета временных параметров сетей и методы преобразования (минимизации) сетей.
Обзор программных средств показал, что существуют популярные программы (Microsoft Project, Spider Project, Project Libre, Gantt Pro, Lucid Chart, EDraw Max и др.), автоматизирующие вычисления для МКП, PERT, способные строить диаграммы Гантта и отображать сетевые графики, а также создавать сопутствующую информацию по различным параметрам модели. При этом наблюдается дефицит программного обеспечения для расчётов альтернативных сетей.
Необходимость применения того или иного типа сетевой модели основывается на специфике реализуемого проекта с учётом требований к качеству и ресурсных ограничений. Тем не менее, нет объективных критериев, позволяющих однозначно выбрать тип модели и методы её анализа.