Классификация сетевых моделей

«Сетевая модель (сетевой график, сеть) представляет собой ориентированный граф, изображающий все необходимые для достижения цели проекта задачи (операции, работы, события, действия) в логической взаимосвязи. Она позволяет осуществлять календарное планирование работ, оптимизировать использование ресурсов, сокращать или увеличивать продолжительность выполнения работ в зависимости от их стоимости, организовывать оперативное управление и контроль в ходе реализации проекта» [6].

Основными формальными элементами любой сетевой модели (СМ) являются узлы и дуги. Функциональные элементы сети – это работы (операции, задачи, этапы) и события (момент начала или окончания операций, вехи), а также структурные зависимости между ними.

Согласно [18], в сетевых технологиях применяются сети трёх типов:

- работы представляются дугами, а события – узлами графа (Activities on Arrows, AoA);

- работы представляются узлами, а события – дугами графа (Activities on Nodes, AoN);

- узлы могут представлять как события, так и работы, а дуги – временные характеристики.

Похожая классификация вводится также в [9], где сетевые модели называют «ориентированными» (на операции, события, события и операции). Другие авторы ([23];[6];[17];[7]) не выделяют третий тип.

Конечно, сетевые модели обладают и другими важными параметрами. Например, в [9] кроме ориентированных на события и работы выделяются также следующие сети:

по количеству конечных целей:

- одноцелевые;

- многоцелевые;

по количеству исходных событий (операций):

- с одним исходным событием (операцией);

- с несколькими исходными событиями (операциями);

по степени неопределённости сети:

- детерминированные;

- стохастические;

по количеству операций:

- малого объёма (менее 1500);

- среднего объёма (от 1500 до 10000);

- большого объёма (более 10000).

Разные авторы по-разному классифицируют сетевые модели в зависимости от наличия вероятностных характеристик у работ (процессов) и времени их выполнения.

Поскольку этот вопрос важен для дальнейшего изложения, приведем сравнительную таблицу классификации по Разу [14] и Голенко-Гинзбургу [4] (Таблица 1.2).

Таблица 1.2.

Сравнительная классификация сетевых моделей.

Оценка процессов	Оценка продолжительности	Классификация по Разу	Классификация по Голенко-Гинзбургу
Точная	Точная	Детерминированные СМ с точной оценкой продолжительности работ	Детерминированные СМ
Точная	Вероятностная	Детерминированные СМ с вероятностной оценкой продолжительности работ	Вероятностные СМ с детерминированной структурой
Вероятностная	Точная	Стохастические СМ	Альтернативные СМ
Вероятностная	Вероятностная

В дальнейшем будем ориентироваться на классификацию Голенко‑Гинзбурга, предполагающую три основных типа сетевых моделей; детерминированные сетевые модели (ДСМ), вероятностные сетевые модели (ВСМ), альтернативные сетевые модели (АСМ).

В последнее время в теории сетевого моделирования используются так называемые обобщенные сетевые модели, в которых допустимы некоторые исключения, принятые в рассмотренных выше (например, допустимы циклы и петли, а также обратные пути).

Графическое представление модели и временная диаграмма удобны для наглядного представления небольшого количества работ, но с ростом числа работ (а в реальных задачах их десятки тысяч) это преимущество теряется. Поэтому для анализа и оптимизации используют матричную форму [8].

Обратим внимание на временные параметры сетевых моделей. Время – одно из главных ограничений любого проекта, и для анализа временных параметров проекта математический аппарат играет не меньшую роль, чем экономический анализ. Разумеется, способы вычисления временных параметров сети существенно зависят от ее типа, определенного детерминированным или вероятностным характером процессов и продолжительностей, чаще всего определяемых на основе статистических данных.

Детерминированная модель

Будем вначале рассматривать детерминированные сетевые модели. Построение любой сетевой модели начинается с определения списка работ (событий) и построения логической взаимосвязи между ними. Если модель не имеет каких-либо числовых показателей и обозначений, она называется структурной сетевой моделью или топологией [14]. После определения топологии происходит оценка аналитических параметров (продолжительности работ, потребностей в ресурсах и др.). Затем проводится анализ и оптимизация модели.

Приведем требования к одноцелевой СМ с одним исходным событием:

- узлы пронумерованы в порядке выполнения, т. е. для каждой дуги ;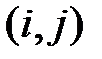

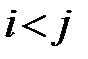- отсутствуют тупиковые узлы (кроме завершающего), т. е. такие, за которыми не следует хотя бы одна дуга;

- отсутствуют узлы (за исключением исходного), которым не предшествует хотя бы одна дуга;

- отсутствуют циклы, т. е. замкнутые цепи, соединяющие узел с ним же самим [20];

- между смежными узлами может проходить только одна дуга;

- узлы строят последовательно (стрелки направлены слева направо – от начала к окончанию);

- следует избегать пересечения дуг на графике;

- фиктивные работы обозначаются пунктирной линией.

Перед построением сетевой модели технологическую последовательность работ заносят в таблицу (

Таблица 1.3).

Таблица 1.3.

Технологическая последовательность работ.
Предшествующие работы ( 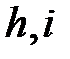)	Данные работы ( )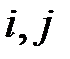
—	0,1
	0,2
	0,3
0,1	1,4
0,1	2,5
0,1	2,6
0,1	3,6
1,4	4,7
2,5	5,7
2,6 3,6	6,8
4,7 5,7	7,8

Построенный по этой таблице сетевой график приведён на

Рис. 1.4.

Рис. 1.4. Сетевой график типа «узел – событие».

Так как сеть – это ориентированный граф, который определяется через бинарное отношение, он также однозначно определяется через матрицы инцидентности [19]. А поскольку работы упорядочены во времени, и дуга связи всегда идёт от события с меньшим номером к событию с большим номером, то достаточно определить матрицу смежности. Расчёт временных и других параметров в компьютерных системах требует табличного или матричного представления проекта. Например, для описанной выше сетевой модели матричное представление выглядит так (Таблица 1.4):

Таблица 1.4.

Матрица сетевого графика.
События

Количество столбцов и строк в матрице равно количеству событий. Каждый столбец и строка нумеруются по порядку согласно количеству событий. Затем на пересечении каждой строки, соответствующей начальному событию, и столбцу, соответствующему последующему событию, ставится «1», а во всех остальных случаях – «0».

Наряду с понятиями работ и событий в сетевом моделировании очень важным является понятие пути.

Путь – это непрерывная последовательность работ между двумя событиям сети. Не каждая пара вершин имеет связывающий их путь.

Полный путь – это непрерывная последовательность работ между исходным и завершающим событием сетевой модели. Суммарная продолжительность работ, лежащих на пути, определяет длину пути [14]. Таких путей в сетевой модели может быть несколько.

Критический путь – это полный путь, длина которого максимальна. В модели может быть несколько критических путей, включающих разные последовательности работ. Примем следующие обозначения для аналитических параметров (Таблица 1.5).

Таблица 1.5.

Аналитические параметры сетевой модели.
№ п/п	Название параметра	Условное обозначение
	Код данной работы	i,j
	Код начального события данной работы	i
	Код конечного события данной работы	j
	Код работы, предшествующей данной	h,i
	Код события, предшествующего работе (i,j)	h
	Код работы, следующей за конечным событием данной работы	j,k
	Код события, следующего за работой j,k	k
	Путь	L
	Продолжительность пути	TL
	Критический путь	Lкр
	Продолжительность критического пути	TLкр
	Продолжительность данной работы	tij
	Раннее начало данной работы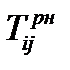
	Раннее окончание данной работы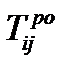
	Позднее начало данной работы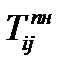
	Позднее окончание данной работы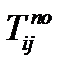
	Общий (полный) резерв времени данной работы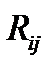
	Свободный резерв времени данной работы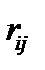

Учитывая время выполнения работы,

Таблица 1.3 дополняется ещё одним столбцом под названием «Продолжительность» (Таблица 1.6).

Ниже представлены графики с временной характеристикой. На Рис. 1.5. Сетевая модель «узел – событие» с изображена модель «узел – событие» (работы на дугах, AoA) с указанием времени выполнения работ.

Таблица 1.6.

Технологическая последовательность работ с учетом продолжительности.
Предшествующие работы ( 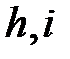)	Данная работа ( 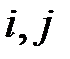)	Продолжительность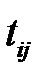
—	0,1
	0,2
	0,3
0,1	1,4
0,1	2,5
0,1	2,6
0,1	3,6
1,4	4,7
2,5	5,7
2,6 3,6	6,8
4,7 5,7	7,8

Рис. 1.5. Сетевая модель «узел – событие» с указанием временных параметров.

Модель «узел – работа» (AoN) имеет существенные отличия от предыдущей. В узле содержится следующая информация (Рис. 1.6).

Рис. 1.6. Параметры, описываемые в узле модели «узел – работа».

На Рис. 1.7 представлена модель «узел – работа», эквивалентная изображённой на Рис. 1.5.

Рис. 1.7. Сетевая модель «узел – работа» с временными параметрами.

Особенностью построения СМ «узел – работа» являются:

- добавление условных узлов «Начало», предшествующего всем узлам и «Окончание», следующего после всех работ (работы в этих узлах имеют нулевую продолжительность);

- работы можно нумеровать одним индексом;

- нет необходимости вводить фиктивные события, обозначающие логическую взаимосвязь событий;

- вычисление аналитических параметров удобно проводить прямо на графике.

Временные параметры работ и событий определяются на основе метода динамического программирования.

Ранние начало работ (время, раньше которого событие наступить не может) определяется последовательно от начального события до конечного. Для работ, выходящих из начального события, раннее начало равно нулю. Чтобы посчитать раннее начало последующих работ, необходимо определить раннее окончание работ, начинающихся от исходного. Раннее окончание вычисляется по формуле

.

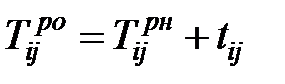(1.1)

Раннее начало данной работы равно максимальному из ранних окончаний предшествующих:

.

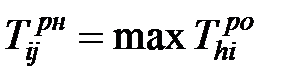(1.2)

Позднее начало и позднее окончание работы вычисляются в обратном порядке, причём поздние окончания работ, предшествующих заключительному событию(работу) выбираются как максимальное раннее окончание из этих работ. Позже этого времени ни одна работа не закончится. Позднее начало работы можно вычислить по формуле

,

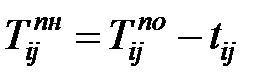(1.3)

а позднее окончание предшествующей работы всегда равняется минимуму из поздних начал последующих:

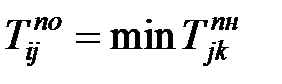(1.4)

Критическими называются работы, лежащие на критическом пути. Для них обязательно выполнение следующих свойств.

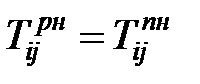,	(1.5)
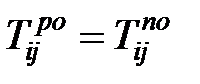.	(1.6)

То есть полный резерв времени работ, который можно вычислить по любой из двух формул

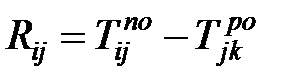,	(1.7)
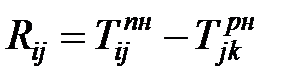,	(1.8)

для критических работ будет равен нулю.

Для остальных работ полный резерв означает, что можно увеличить её длительность или начать работу позже. Полный резерв принадлежит не конкретной работе, а всему пути, содержащему эту работу. Поэтому логично, что для любого пути, не являющегося критическим, вводится понятие общего (полного) резерва времени, который будет равен разнице между длиной критического и данного пути:

.

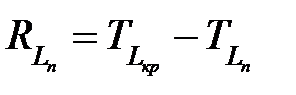(1.9)

Частный (свободный) резерв определяет, на сколько можно сдвинуть работу или увеличить её длительность, чтобы не повлиять на раннее начало других работ и общие резервы всех последующих работ, которые находятся на том же пути, что и данная. Частный резерв вычисляется по формуле

.

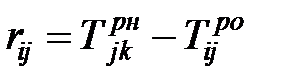(1.10)

Независимый резерв времени – это часть полного резерва при условии, что предшествующие работы завершаются в поздний срок, а последующие начинаются в ранний срок. Независимый резерв времени принадлежит только данной работе.

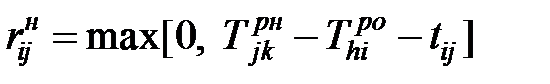(1.11)

Для ручного способа расчёта сетевого графика может использоваться таблица следующего типа (Таблица 1.7):

Таблица 1.7.

Расчёт аналитических параметров сетевого графика.

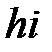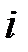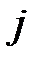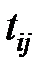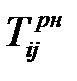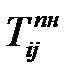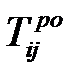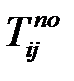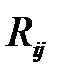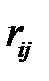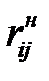В столбец 1 записывают количество предшествующих работ, в столбец 2 – номер начального события, в столбец 3 – номер конечного события, в столбец 4 – время выполнения работы. Остальные столбцы рассчитываются согласно описанным выше правилам. Для модели из примера расчётная таблица будет иметь следующий вид (Таблица 1.8).

Таблица 1.8.

Расчет временных параметров

—
—
—
		—	—					—	—	—

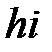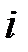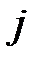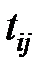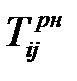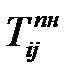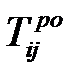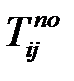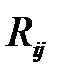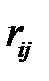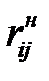Из приведенной таблицы легко увидеть, что путь «0 – 2 – 6 – 8» является критическим, так как резервы времени равны работ нулю (в таблице работы, находящиеся на этом пути, выделены).

Для каждого проекта выбирается своя единица времени в зависимости от масштаба и необходимой точности. Основной целью введения временных параметров является определение продолжительности проекта (длина критического пути), длительности остальных путей, временных резервов путей и отдельных работ с целью дальнейшей оптимизации модели.

Если известна продолжительность каждой работы, можно вычислить длительность всего проекта. Один из базовых и наиболее простых методов анализа – Метод критического пути (МКП) заключается в определении работ (событий), которые должны быть выполнены (наступить) точно в срок, их длительности не могут быть увеличены без увеличения длительности всего проекта. На такие работы обычно направляется больше ресурсов.

Когда все временные параметры вычислены, остаётся только обозначить критический путь на графике. Расчёт критического пути можно проводить, используя особые способы записи на самом графике (четырёхсекторный метод, дробный метод, метод потенциалов). Все методы эквивалентны, так как используют единый аппарат расчёта [11, с. 254].

Вероятностная модель

Рассмотрим теперь случай, когда топология сети детерминирована, а продолжительность работ имеет вероятностную оценку. Методы для расчёта такого типа моделей впервые применялись в рамках методики PERT, о которой уже упоминалось выше.

Пусть продолжительность любой из работ – случайная величина, обладающая такими характеристиками, как средняя продолжительность 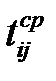и дисперсия работы .

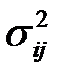Очевидно, что в данном случае на распределение длительности работ накладывается ряд ограничений. Это распределение должно быть неотрицательным, унимодальным, конечным и непрерывным [4]. Для расчёта продолжительности используют так называемые «экспертные» оценки длительности:

- наиболее вероятная 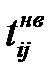(в формулах – m);

- пессимистичная 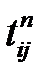(в формулах – b);

- оптимистичная 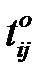(в формулах – a).

На основе многочисленных исследований, отмеченных в [3, с. 8], определено, что в качестве закона распределения можно использовать бета-распределение, которое удовлетворяет всем указанным условиям.

Функция плотности бета-распределения определяется на отрезке 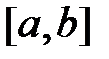следующим образом:

,

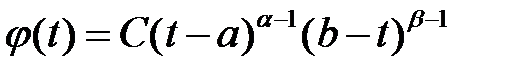(1.12)

где

;

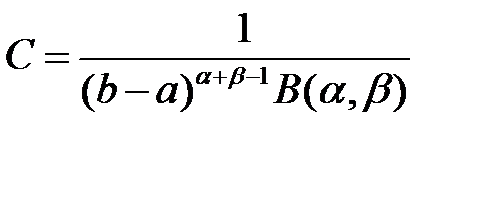(1.13)

в свою очередь бета-функция –

,

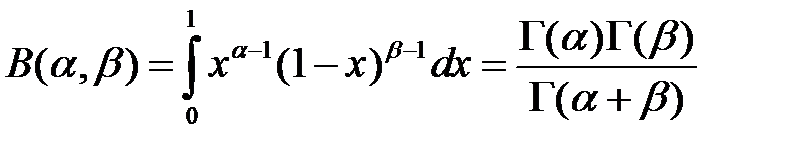(1.14)

где гамма-функция определяется по формуле

.

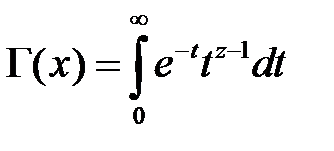(1.15)

Расчёт коэффициентов бета-функции α и β производится по следующим формулам.

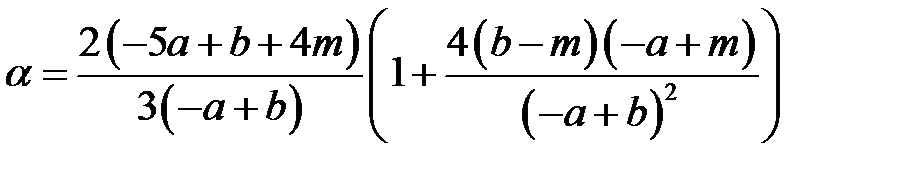,	(1.16)
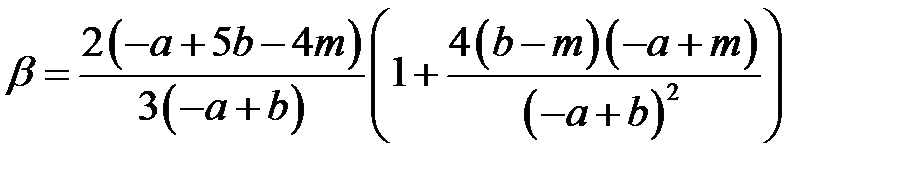,	(1.17)

где a – оптимистичная продолжительность работы,

b – пессимистичная продолжительность работы,

m – наиболее вероятная продолжительность работы.

На

Рис. 1.8 изображены график функции плотности вероятности (а) и функции распределения (б) для бета-распределения с параметрами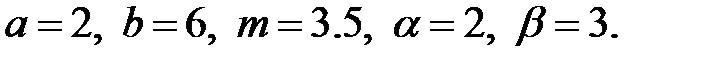

- а) плотность;

б) функция распределения.

Рис. 1.8. Бета-распределение.

Правила вывода формул (1.16) и (1.17) описаны в [22]. Следует отметить, что средняя продолжительность работы является математическим ожиданием 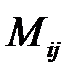случайной величины «длительность работы» и вычисляется по формуле

.

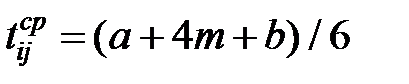(1.18)

Дисперсия оценки продолжительности работы определяется так:

.

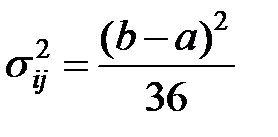(1.19)

Таким образом, 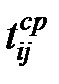характеризует наиболее вероятную длительность операции, тогда как 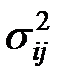определяет величину диапазона возможных длительностей. Чем меньше величина дисперсии, тем меньше неопределённость длительности работы.

Согласно [4], формулы (1.18) и

(1.19) «носят полуэмпирический характер». Голенко-Гинзбургом в качестве альтернативы методам расчёта PERT была предложена модель на основе двух оценок, которая значительно упрощает процесс расчёта и имеет ряд преимуществ перед технологией PERT [4, с. 17], а статистический анализ проекта в этом случае показывает несущественные изменения.

Плотность распределения определена следующим образом:

,

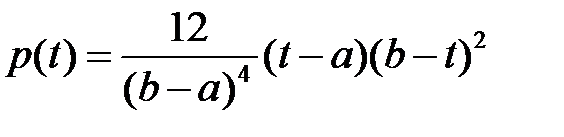(1.20)

средняя длительность работы:

,

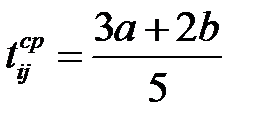(1.21)

дисперсия:

.

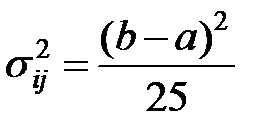(1.22)

Некоторые авторы предлагают различные альтернативы методу PERT, например метод А. А. Мешкова [5].

Ожидаемую длительность проекта вычисляют как среднюю продолжительность критического пути – это сумма средних длительностей работ, лежащих на этом пути, а отклонение длительности – сумма отклонений работ:

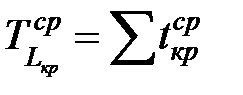.	(1.23)
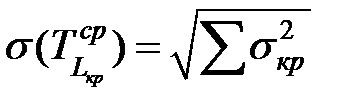.	(1.24)

Но величина 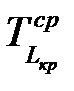не всегда удовлетворительна, поэтому дополнительно выбирают директивную продолжительность 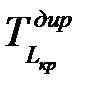[14], и оценивают вероятность завершения работы до предписанного срока :

,

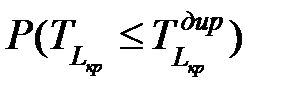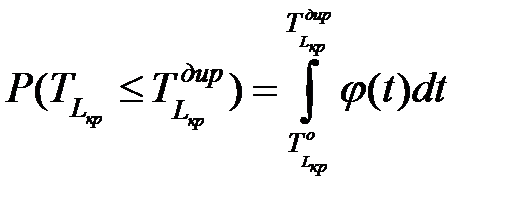(1.25)

где 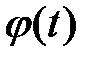– функция плотности,

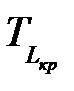– продолжительность критического пути,

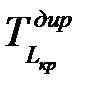– директивная длительность критического пути,

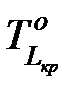– оптимистичная (наименьшая) продолжительность критического пути.

PERT-анализ обладает рядом недостатков, из-за которых вместо него выбирают альтернативные решения. Среди недостатков метода:

- субъективная оценка продолжительности работ;

- выбранная функция распределения для вычисления средней продолжительности работ часто не совпадает с реальным законом распределения;

- для продолжительных проектов оценка с помощью PERT при разработке может кардинально отличаться от оценки, проводимой на одном из этапов реализации (требуются постоянные корректировки);

- неточная оценка критического пути: работы не на критическом пути с большой дисперсией могут стать критическими во время выполнения.