Связь рассматриваемой в настоящем пункте задачи о геометрической прочности сетей и теории просачивания заключается в следующем.

Обозначим через 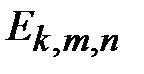количество всех ребер графа 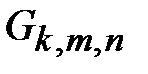; 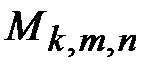– математическое ожидание количества ребер из графа 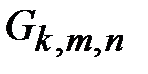, которое следует случайным образом добавить к пустому графу 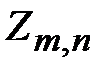, чтобы в получившемся графе появился путь, соединяющий левую и правую сторону сетки 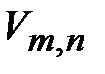. Пусть, далее, 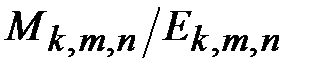– отношение соответствующего математического ожидания к количеству ребер регулярного графа; 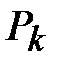– граничная вероятность “открытости ребра” графа 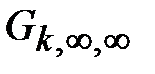, при превышении которой в этом графе с вероятностью 1 имеется сколь угодно длинный путь из произвольной вершины, уходящий в бесконечность.

Следующее рассуждение показывает, что при достаточно больших n, то есть при достаточно больших размерах рассматриваемых сетей, должно выполняться неравенство .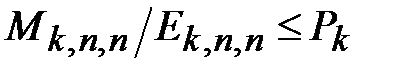

Действительно, после добавления случайным образом 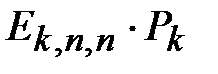штук ребер графа 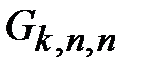к графу 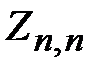, вероятность наличия в получившемся графе «сколь угодно длинного пути» из некоторой фиксированной вершины на левой стороне сетки станет равной 1, то есть в получившемся графе найдется путь из этой вершины на левой стороне сетки к её правой стороне. Поскольку различных вершин, из которых могут строиться пути на правую сторону, на левой стороне сетки n штук, получаем требуемое неравенство 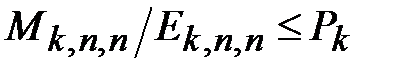(которое могло бы стать равенством при n=1, то есть на левой стороне сетки была бы всего одна вершина).

Таким образом, пороги просачивания для бесконечных регулярных графов из теории протекания являются верхними границами для соответствующих параметров 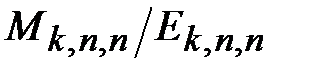в задачах о геометрической прочности регулярных сетей. При этом, на основании приведенных рассуждений, трудно ожидать, что для сеток, на сторонах которых имеется более одной вершины, эти границы являются точными или, более того, отношение 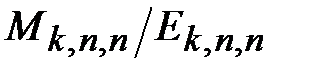может оказаться в точности равным порогу просачивания.

Именно поэтому, немалое удивление вызывают результаты компьютерных экспериментов для квадратных сеток, приведенные в п.2.3.4. Они показывают, что для графов со степенью вершин больше 3, выполняется точное равенство 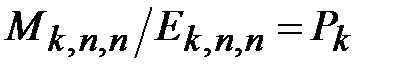, что указывает на непосредственную связь результатов проведенных экспериментов по определению геометрической прочности сетей с результатами теории просачивания. Становится ясно, что имеется некая общая сущность природы явлений, изучаемых как в теории просачивания, так и в задачах о геометрической прочности сетей, вскрытие и изучение которой является чрезвычайно интересным и перспективным направлением фундаментальных научных исследований.

Для графов со степенью вершин 3 видны (см. п. 2.3.4) незначительные отклонения от указанного равенства, которые, скорее всего, объясняются небольшими размерами сеток, для которых проводились компьютерные испытания. Было бы чрезвычайно интересно провести расчеты на регулярных (степени вершин 3) сетях большего размера, чем 100 на 100. Это дало бы возможность подтвердить или опровергнуть интригующее равенство 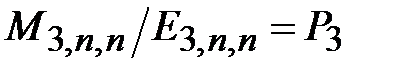, устанавливающее связь задачи о геометрической прочности сетей с теорией просачивания и для случая регулярных сетей с вершинами степени три, но вычислительные возможности компьютеров, использованных при проведении экспериментов, оказались для этого недостаточны.