Обсуждение и постановка задачи характеризации
Градуированных сетей
В настоящем пункте рассматриваются организационные сети – классическое понятие теории управления и организации производства [4]. Традиционно, сети принято изображать диаграммами [1,2]. Диаграмма сети представляет собой размещенный на плоскости (или, при необходимости, для достижения наглядности при моделировании и представлении сложных сетей – в трехмерном пространстве) граф [2] 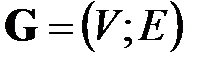 , где
, где 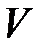 – множество вершин, интерпретируемых как узлы организационной сети (предприятия, организации, структурные единицы),
– множество вершин, интерпретируемых как узлы организационной сети (предприятия, организации, структурные единицы), 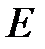 – множество ребер этого графа, интерпретируемых как организационные связи между составляющими сеть узлами.
– множество ребер этого графа, интерпретируемых как организационные связи между составляющими сеть узлами.
В предыдущем разделе 2.1 введено понятие градуированной организационной сети [8–10] и показано, что большинство встречающихся в практической деятельности организационных сетей, является градуированными. В настоящем пункте сузим общее понятие градуировки сети с помощью произвольного частично-упорядоченного множества и будем рассматривать только градуировки сетей с помощью натуральных чисел. Таким образом, градуированная организационная сеть 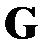 – это сеть, имеющая гомоморфизм
– это сеть, имеющая гомоморфизм 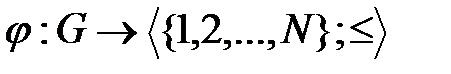 на начальный отрезок натурального ряда
на начальный отрезок натурального ряда 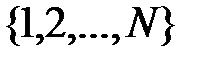 , упорядоченный естественным образом отношением порядка
, упорядоченный естественным образом отношением порядка 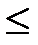 . Содержательно, отображение
. Содержательно, отображение 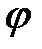 присваивает элементам (предприятиям) сети
присваивает элементам (предприятиям) сети 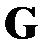 некоторое натуральное число – приоритет, или ранг, означающий важность и значимость предприятия в сети с точки зрения его производственных функций.
некоторое натуральное число – приоритет, или ранг, означающий важность и значимость предприятия в сети с точки зрения его производственных функций.
Условимся считать, что чем важнее предприятие 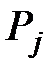 сети
сети 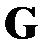 с точки зрения стоящих перед сетью производственных задач, тем меньше его ранг
с точки зрения стоящих перед сетью производственных задач, тем меньше его ранг 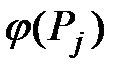 как натуральное число. Таким образом, наиболее важные узлы сети – предприятия «первого ранга», а менее значимые предприятия получают «более низкие ранги», выражаемые большими по величине натуральными числами. Наличие градуировки (или её потенциальная возможность) является отличительной особенностью большинства реальных организационных сетей [8,10].
как натуральное число. Таким образом, наиболее важные узлы сети – предприятия «первого ранга», а менее значимые предприятия получают «более низкие ранги», выражаемые большими по величине натуральными числами. Наличие градуировки (или её потенциальная возможность) является отличительной особенностью большинства реальных организационных сетей [8,10].
В п. 2.1.2 было отмечено, что если имеется градуировка 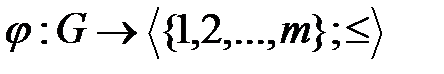 сети
сети  , то сеть
, то сеть  естественным образом разбивается на классы
естественным образом разбивается на классы 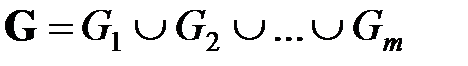 узлов одинакового ранга Будем называть классы разбиения уровнями. Имеем
узлов одинакового ранга Будем называть классы разбиения уровнями. Имеем 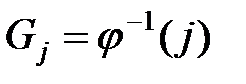 , то есть на уровне
, то есть на уровне 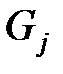 содержатся все узлы сети
содержатся все узлы сети  , имеющие ранг
, имеющие ранг  . Уровни
. Уровни 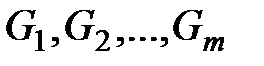 удобно представлять в виде расположенных друг над другом горизонтальных плоскостей, на каждой из которых находятся все узлы сети, ранг которых равен номеру этой плоскости [10].
удобно представлять в виде расположенных друг над другом горизонтальных плоскостей, на каждой из которых находятся все узлы сети, ранг которых равен номеру этой плоскости [10].
| Рис.2.4. Примеры диаграмм градуированных организационных сетей разных типов и их разбиение на уровни |
| Иерархическая организационная структура |
| Радиально-планетарная организационная структура |
градуировка 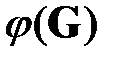 |
градуировка 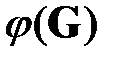 |
Примеры диаграмм градуированных сетей и их разбиений на уровни приведены на рисунке 2.4.
На рисунке 2.4 изображены примеры градуированных диаграмм иерархической структуры и радиально-планетарной организационной сети, рассматривавшихся в [4,11]. Видно, что ребра (организационные связи) идут из вершин данного ранга в вершины следующего ранга, но не «перескакивают» через уровень – это запрещено по определению градуированной сети.
Стандартным общеупотребительным способом задания сетей и хранения их в электронном виде является представление сетей матрицами смежности (или матрицами потоков). Пусть дана сеть 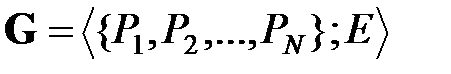 , узлы
, узлы 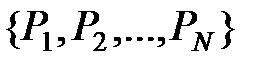 которой занумерованы последовательными натуральными числами (здесь
которой занумерованы последовательными натуральными числами (здесь 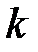 – номер узла
– номер узла 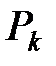 ,
, 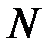 – число узлов сети
– число узлов сети 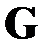 ). Напомним, что матрица смежности
). Напомним, что матрица смежности 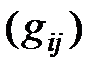 сети
сети 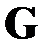 имеет размеры
имеет размеры 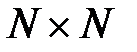 и определяется следующим образом [2]:
и определяется следующим образом [2]:
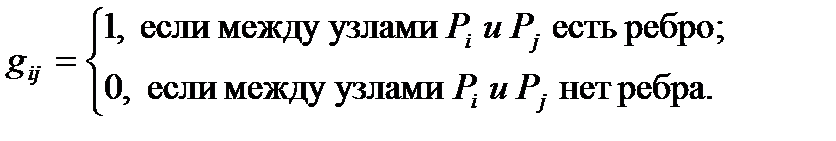
Матрицы смежности графов и сетей – наиболее распространенный и общеизвестный способ представления сетей, приспособленный для хранения конфигурации сетей в компьютерном виде. Известно, что всякая сеть определяется своей матрицей смежности однозначно, с точностью до изоморфизма [2], то есть матрица смежности 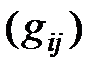 задаёт диаграмму сети
задаёт диаграмму сети 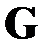 (узлы и связи) однозначно, с точностью до расположения узлов на плоскости и формы линий, соединяющих эти узлы. Этими обстоятельствами объясняется повсеместное использование матриц смежности для хранения, анализа и компьютерной обработки информации об организационных сетях и иных сетевых структурах.
(узлы и связи) однозначно, с точностью до расположения узлов на плоскости и формы линий, соединяющих эти узлы. Этими обстоятельствами объясняется повсеместное использование матриц смежности для хранения, анализа и компьютерной обработки информации об организационных сетях и иных сетевых структурах.
Однако, как нетрудно видеть, метод представления сетей матрицами смежности страдает существенными недостатками. Прежде всего, матричный метод является избыточным способом (особенно при наличии априорной дополнительной информации об устройстве сети и виде её диаграммы). Значительные объемы памяти в матрицах смежности занимают одинаковые числа, матрицы имеют большие размеры, вычисления с помощью матриц смежности неудобны и страдают отсутствием наглядности. Если сеть содержит 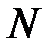 узлов, то её матрица смежности состоит из
узлов, то её матрица смежности состоит из 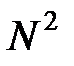 чисел, что значительно затрудняет и увеличивает время работы различных стандартных алгоритмов анализа сетей (в особенности, алгоритмов переборного характера, например таких, как алгоритм поиска гамильтонова цикла или маршрута коммивояжера). Уже при
чисел, что значительно затрудняет и увеличивает время работы различных стандартных алгоритмов анализа сетей (в особенности, алгоритмов переборного характера, например таких, как алгоритм поиска гамильтонова цикла или маршрута коммивояжера). Уже при 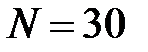 , матрица смежности содержит
, матрица смежности содержит 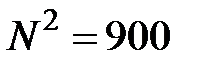 элементов и алгоритм полного перебора на такой матрице будет работать и получать результат за время порядка
элементов и алгоритм полного перебора на такой матрице будет работать и получать результат за время порядка 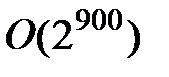 тактов, что при современном состоянии компьютерной техники составляет триллионы лет – с практической точки зрения, время работы такого алгоритма бесконечно и совершенно неприемлемо.
тактов, что при современном состоянии компьютерной техники составляет триллионы лет – с практической точки зрения, время работы такого алгоритма бесконечно и совершенно неприемлемо.
Избыточность метода представления сетей матрицами смежности объясняется его универсальностью и возможностью его применения в любых ситуациях. Разумно предположить, что для случая конкретных организационных сетей (например, градуированных) существует более простой, наглядный и эффективный способ их представления, сохраняющий, тем не менее, все преимущественные и полезные свойства матричного представления сетей. Кроме того, относительно предполагаемого нового метода, разумно выдвинуть требования простоты и высокой скорости выполнения стандартных алгоритмов анализа сетей при использовании их представления по новому методу.
В работе [12] были введены группы усредненных геометрических характеристик для сетей специфического вида, являющихся орбитальными планетарными структурами. Там же была поставлена общая задача об определяемости организационных сетей по наборам их геометрических характеристик.
В настоящем разделе решаются все эти задачи. Вводятся новые и обобщаются приведенные в [12] группы геометрических характеристик для случая произвольных градуированных организационных сетей. На основании введенных геометрических характеристик, предлагается новый метод представления организационных сетей, полностью удовлетворяющий сформулированным выше требованиям к однозначности, алгоритмической простоте, наглядности и эффективности метода.
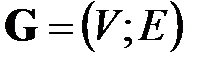 , где
, где 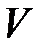 – множество вершин, интерпретируемых как узлы организационной сети (предприятия, организации, структурные единицы),
– множество вершин, интерпретируемых как узлы организационной сети (предприятия, организации, структурные единицы), 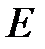 – множество ребер этого графа, интерпретируемых как организационные связи между составляющими сеть узлами.
– множество ребер этого графа, интерпретируемых как организационные связи между составляющими сеть узлами.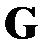 – это сеть, имеющая гомоморфизм
– это сеть, имеющая гомоморфизм 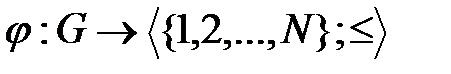 на начальный отрезок натурального ряда
на начальный отрезок натурального ряда 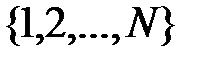 , упорядоченный естественным образом отношением порядка
, упорядоченный естественным образом отношением порядка 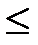 . Содержательно, отображение
. Содержательно, отображение 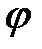 присваивает элементам (предприятиям) сети
присваивает элементам (предприятиям) сети 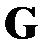 некоторое натуральное число – приоритет, или ранг, означающий важность и значимость предприятия в сети с точки зрения его производственных функций.
некоторое натуральное число – приоритет, или ранг, означающий важность и значимость предприятия в сети с точки зрения его производственных функций.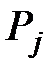 сети
сети 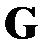 с точки зрения стоящих перед сетью производственных задач, тем меньше его ранг
с точки зрения стоящих перед сетью производственных задач, тем меньше его ранг 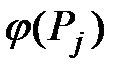 как натуральное число. Таким образом, наиболее важные узлы сети – предприятия «первого ранга», а менее значимые предприятия получают «более низкие ранги», выражаемые большими по величине натуральными числами. Наличие градуировки (или её потенциальная возможность) является отличительной особенностью большинства реальных организационных сетей [8,10].
как натуральное число. Таким образом, наиболее важные узлы сети – предприятия «первого ранга», а менее значимые предприятия получают «более низкие ранги», выражаемые большими по величине натуральными числами. Наличие градуировки (или её потенциальная возможность) является отличительной особенностью большинства реальных организационных сетей [8,10].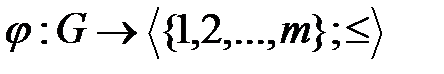 сети
сети  , то сеть
, то сеть  естественным образом разбивается на классы
естественным образом разбивается на классы 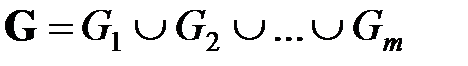 узлов одинакового ранга Будем называть классы разбиения уровнями. Имеем
узлов одинакового ранга Будем называть классы разбиения уровнями. Имеем 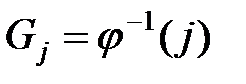 , то есть на уровне
, то есть на уровне 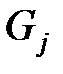 содержатся все узлы сети
содержатся все узлы сети  , имеющие ранг
, имеющие ранг  . Уровни
. Уровни 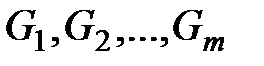 удобно представлять в виде расположенных друг над другом горизонтальных плоскостей, на каждой из которых находятся все узлы сети, ранг которых равен номеру этой плоскости [10].
удобно представлять в виде расположенных друг над другом горизонтальных плоскостей, на каждой из которых находятся все узлы сети, ранг которых равен номеру этой плоскости [10].

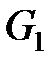
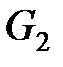
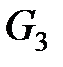
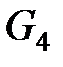
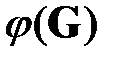
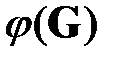
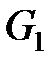
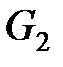
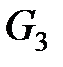
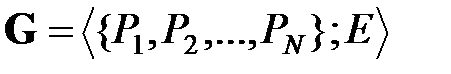 , узлы
, узлы 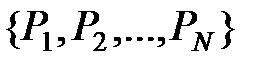 которой занумерованы последовательными натуральными числами (здесь
которой занумерованы последовательными натуральными числами (здесь 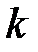 – номер узла
– номер узла 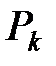 ,
, 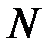 – число узлов сети
– число узлов сети 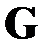 ). Напомним, что матрица смежности
). Напомним, что матрица смежности 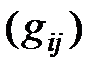 сети
сети 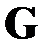 имеет размеры
имеет размеры 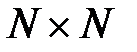 и определяется следующим образом [2]:
и определяется следующим образом [2]: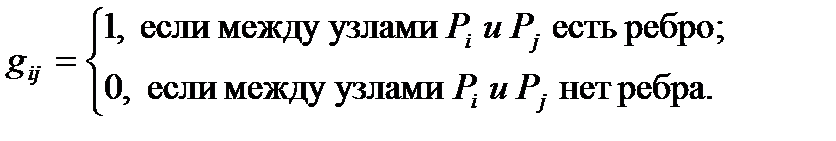
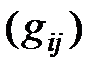 задаёт диаграмму сети
задаёт диаграмму сети 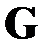 (узлы и связи) однозначно, с точностью до расположения узлов на плоскости и формы линий, соединяющих эти узлы. Этими обстоятельствами объясняется повсеместное использование матриц смежности для хранения, анализа и компьютерной обработки информации об организационных сетях и иных сетевых структурах.
(узлы и связи) однозначно, с точностью до расположения узлов на плоскости и формы линий, соединяющих эти узлы. Этими обстоятельствами объясняется повсеместное использование матриц смежности для хранения, анализа и компьютерной обработки информации об организационных сетях и иных сетевых структурах.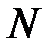 узлов, то её матрица смежности состоит из
узлов, то её матрица смежности состоит из 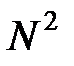 чисел, что значительно затрудняет и увеличивает время работы различных стандартных алгоритмов анализа сетей (в особенности, алгоритмов переборного характера, например таких, как алгоритм поиска гамильтонова цикла или маршрута коммивояжера). Уже при
чисел, что значительно затрудняет и увеличивает время работы различных стандартных алгоритмов анализа сетей (в особенности, алгоритмов переборного характера, например таких, как алгоритм поиска гамильтонова цикла или маршрута коммивояжера). Уже при 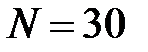 , матрица смежности содержит
, матрица смежности содержит 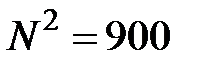 элементов и алгоритм полного перебора на такой матрице будет работать и получать результат за время порядка
элементов и алгоритм полного перебора на такой матрице будет работать и получать результат за время порядка 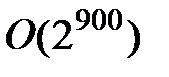 тактов, что при современном состоянии компьютерной техники составляет триллионы лет – с практической точки зрения, время работы такого алгоритма бесконечно и совершенно неприемлемо.
тактов, что при современном состоянии компьютерной техники составляет триллионы лет – с практической точки зрения, время работы такого алгоритма бесконечно и совершенно неприемлемо.