П.2. Свойства неопределенного интеграла
П. 1. Первообразная и неопределенный интеграл
Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции
F'(x) = f(x).
Обозначение
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.
П.2. Свойства неопределенного интеграла
1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
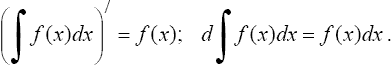
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
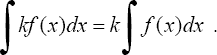
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.
Метод интегрирования по частям основан на следующей формуле:
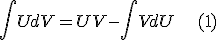
где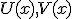 
- непрерывно дифференцируемые функции.
Формула (1) называется формулой интегрирования по частям. Применять ее целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. Отметим, что в некоторых случаях формулу (1) необходимо применять несколько раз.
Метод интегрирования по частям рекомендуется использовать для нахождения интегралов от функций:
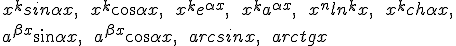
и т.д. где 
- целые положительные постоянные, 
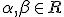, а также для отыскания некоторых интегралов от функций, содержащих обратные тригонометрические и логарифмические ф
Вычисление работы с помощью определенного интеграла
Пусть под действием некоторой силы 
(данная функция непрерывна на отрезке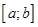 
) материальная точка М движется по прямой OS, работа силы по перемещению точки на отрезке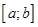
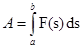
Пример:
Сила, действующая на материальную точку меняется по закону 
, найти работу данной силы при перемещении тела из координаты x=2 до координаты х=7
Пусть на плоскости Oxy дана система материальных точек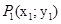 
, 
, …, 
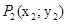с массами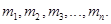 
координаты центра тяжести в данном случае будут определяться по формулам
, 
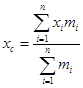Центр тяжести плоской линии
Пусть задана кривая АВ уравнением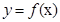 
, 
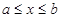, и пусть эта кривая представляет собой материальную линию.
Координаты центра тяжести данной линии
П. 1. Первообразная и неопределенный интеграл
Первообразной функцией для функции f(x) называется такая функция F(х), производная которой равна данной функции
F'(x) = f(x).
Обозначение
где F'(x) = f(x). Функция f(x) называется подынтегральной функцией, а выражение f(x)dx - подынтегральным выражением.
П.2. Свойства неопределенного интеграла
1°. Производная неопределенного интеграла равна подынтегральной функции; дифференциал от неопределенного интеграла равен подынтегральному выражению, т.е.
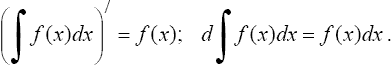
2°. Неопределенный интеграл от дифференциала некоторой функции равен сумме этой функции и произвольной постоянной, т.е.
3°. Постоянный множитель можно вынести из под знака интеграла, т.е. если k = const ≠ 0, то
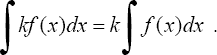
4° . Неопределенный интеграл от алгебраической суммы двух функций равен алгебраической сумме интегралов от этих функций в отдельности.
Метод интегрирования по частям основан на следующей формуле:
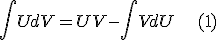
где 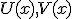- непрерывно дифференцируемые функции.
Формула (1) называется формулой интегрирования по частям. Применять ее целесообразно, когда интеграл в правой части формулы более прост для нахождения, нежели исходный. Отметим, что в некоторых случаях формулу (1) необходимо применять несколько раз.
Метод интегрирования по частям рекомендуется использовать для нахождения интегралов от функций:
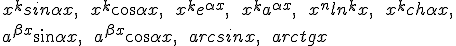
и т.д. где - целые положительные постоянные, 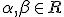, а также для отыскания некоторых интегралов от функций, содержащих обратные тригонометрические и логарифмические ф