Методика изучения арифметических действий в пределах 1000

Все действия в пределах 1000 без перехода через разряд уча­щиеся выполняют приемами устных вычислений с записью в строчку, а с переходом через разряд — приемами письменных вычислений с записью в столбик. Важно постепенное нарастание трудности при решении арифметических примеров. Каждый после­дующий случай в решении примеров должен опираться на знание предыдущих случаев. Непреодолимые трудности для умственно отсталого ребенка могут возникнуть при решении трудных случа­ев, если пропустить одно из звеньев в цепи решения примеров. Поэтому очень важно соблюдать последовательность в выборе примеров, учитывая их нарастающую степень трудности, и тща­тельно отрабатывать каждый случай.

СЛОЖЕНИЕ И ВЫЧИТАНИЕ В ПРЕДЕЛАХ 1000

В изучении действий сложения и вычитания в пределах 1000 можно выделить следующие этапы:

I. Сложение и вычитание без перехода через разряд (устно).

1. Сложение и вычитание круглых сотен. 192

300-100 500-200

200+100 300+200

Действия производятся на основе знания нумерации и сводятся лцеству к действиям в пределах 10. Рассуждения проводятся 200 — это 2 сотни, 100 — это 1 сотня.

— это 300. 200+100=300

.-! сот. + 1 сот.=3 сот. 3 сотни

500-200=?

5 сот.-2 сот.=3 сот.=300

500-200=300

Отдельным учащимся, которые еще нуждаются в использова­нии средств наглядности, можно предложить пучки палочек (1000 "милочек, связанных в пучки по сотне), пластины из арифметичес­кого ящика, полоски длиной 1 м, разделенные каждая на 100 см, н'>ак, счеты.

Полезно решение и составление троек примеров вида

7- 5= 70- 50= 700-500=

4+ 2 =

40+ 20=

400+200=

| последующим сопоставлением компонентов и результатов дейст­вий.

2. Сложение и вычитание круглых сотен и единиц, круглых
< отен и десятков (действия основываются на знании нумерации):

а) 300+ 5 305- 5 б) 300+ 40 340- 40

5+300 305-300 40+300 340-300

в) 300+ 45 345- 45

45+300 345-300

3. Сложение и вычитание круглых десятков, а также круглых
с отен и десятков:

а) 430+ 20 в) 430+120

450- 20 550-120

б) 430+200 630-200

При решении случаев а), б) рассуждения проводятся так: «430 — это 4 сот. и 3 дес., 20 — это 2 дес. Складываем десятки: 3 дес.+2 дес. = 5 дес. 4 сот.+5 дес.=450».

Разряды, которые складываются или вычитаются, можно реко­мендовать подчеркивать:

430+200=630 630-200=430

Перова М. Н.

При решении примеров вида в) рассуждения проводятся т|| «120=100+20, 430+100=530, 530+20=550», т. е. этот случ( сложения (вычитания) сводится к уже известным учащимся с/ чаям сложения (вычитания) а), б).

4. Сложение трехзначных чисел с однозначным, двузначным | трехзначным без перехода через разряд и соответствующие сл\ чаи вычитания:

а) 540+5 543+2	545-5 545-2	б) 545+40 585-40	в) 350+23 356+23	373-23 379-23
г) 350+123	673-123
356+123	679-123

Выполнение действий производится устно. Учащиеся при выпол« нении действий пользуются теми же приемами, какими они пользо^ вались при изучении действий сложения и вычитания в пределах! 100, т. е. раскладывают второй компонент действия (второе слагав-; мое или вычитаемое) на разрядные единицы и последовательно их] складывают или вычитают из первого компонента.

Например:

350+123

673-123

123=100+20+3 673-100=573 573- 20=553 553- 3=550

123=100+20+3 350+100=450 450+ 20=470 470+ 3=473

5. Особые случаи сложения и вычитания. К ним относятся 1 случаи, которые вызывают наибольшие трудности и в которых ] чаще всего допускаются ошибки. Учащихся больше всего затруд­няют действия с нулем (нуль находится в середине числа или в конце). Случай с числами, содержащими нуль, не требует особых приемов. Но таких примеров надо решать больше, повторить перед решением таких примеров решение примеров на сложение и вычитание, когда компонентом действия является нуль: 0+3, 5+0, 5-5:

а) 308+121 б) 402-201 в) 736-504

308+100=408 402-200=202 736-500=236

408+ 20=428 202- 1=201 236- 4=232
428+ 1=429

г) 0+436 700-0 725-725

^х'стные приемы вычислений требуют от учащихся постоянного шза чисел по их десятичному составу, понимания места ры в числе, понимания того, что действия можно производить ко над одноименными разрядами. Не всем учащимся вспомо-льной школы это становится понятным одновременно. 11еред выполнением действий необходимо добиваться от уча-ц\ся предварительного анализа десятичного состава чисел. Учи-и- п. чаще должен ставить вопросы: «С чего надо начинать сложе-|пм"> Какие разряды складываем?»

15 противном случае учащиеся допускают ошибки при вычисле­ниях. Они складывают десятки с сотнями, а результат записывают "|Ц)0 в разряд сотен, либо в разряд десятков, например: 100+10=500, 30+400=70, 30+400=470, 30+400=340, (./0+2=690, 670-3=640.

Эти ошибки свидетельствуют о непонимании позиционного зна­чения цифр в числе, о неумении самостоятельно контролировать результаты действий. Учителю необходимо добиваться того, чтобы учащиеся проверяли выполнение действий, причем делали это не формально, а по существу. Нередко приходится наблюдать, что ученик якобы и сделал проверку, но выполнил ее формально. Он написал только обратное действие, а не решал, поэтому и не заметил допущенной ошибки, например: 490—280=110. Проверка. 110+280=490.

Нередко можно столкнуться с непониманием умственно отста­лыми школьниками (даже старших классов) сущности проверки. Проверка часто выполняется учениками только потому, что этого либо требует учитель, либо такое задание содержится в учебнике. Часто при выполнении проверки ученик получает несоответствие между полученным результатом и заданным примером, но это не служит ему поводом для исправления неверного ответа, например: 570-150=320. Проверка. 320+150=470.

В данном случае проверка выступает как самостоятельное дей­ствие, никак не связанное с тем, которое ученик проверяет.

Учитель постоянно должен помнить об этих ошибках школьни­ков с нарушением интеллекта и требовать ответа на вопросы: «Что показала проверка? Верно ли решен пример? Как доказать, что действие выполнено верно?»

Осознанному выполнению устных вычислений, выработке обоб­щенных способов выполнения действий служит постоянное внима-

ние к вопросам сравнения и сопоставления разных по трудно случаев сложения, вычитания. Важно научить учащихся вид| общее и особенное в тех примерах, которые они решают.

Например, сравнить примеры и объяснить их решение:

30+5, 300+40, 300+45, 300+140, 300+145, 300+105.

305-5, 340-40, 345-45, 340-300, 345-300, 345-200.

Полезно и составление учащимися примеров, аналогичных (г хожих) данным, или примеров определенного вида: «Составьт! пример, в котором надо сложить круглые сотни с единицами»;! «Составьте пример на вычитание, в котором уменьшаемое — | трехзначное число, а вычитаемое — круглые десятки» и т. д.¹

Для закрепления действий сложения и вычитания в предела» 1000 приемами устных вычислений полезно решение примеров с| неизвестными компонентами.

II. Сложение и вычитание с переходом через) разряд.

Сложение и вычитание с переходом через разряд — это наибо«| лее трудный материал. Поэтому учащиеся выполняют действия столбик. Сложение и вычитание в столбик производятся над каж-| дым разрядом в отдельности и сводятся к сложению и вычитании в пределах 20. Но в этом случае возникают у умственно отсталь школьников трудности в записи чисел, т. е. в умении правильно подписать разряд под соответствующим разрядом.

Часто из-за неумения организовать внимание, из-за недостаточно четкого понимания позиционного значения цифр в числе, а то и из-за небрежности при записи цифр ученики сдвигают число, которое нужно прибавить или вычесть, влево или вправо и поэтому допуска-; ют ошибки в вычислениях. Особенно много ошибок учащиеся допус­кают при записи чисел в столбик, если действие производится над трехзначным и двузначным или однозначным числом. В этом случае десятки подписываются под сотнями, единицы под сотнями или де­сятками. Это приводит к ошибкам в вычислениях.

Например:

375 375 238

⁺ 6 ⁺38 ~18

~~975~ "775" 58

Наибольшие трудности вызывает действие вычитания. Ошибки в вычислениях носят различный характер. Причиной некоторых из

Слабоуспевающим учащимся разрешается выполнение всех случаев в стол-

бик.

Ихявляется слабое усвоение табличного сложения и вычитания

I пределах 20.

238 275

+__ 7 ~ 7

246 26ТГ

Много ошибок допускается в результате того, что ученики
убывают прибавить получившийся в уме десяток или сотню, а
Также забывают, что «занимали» сотню или десяток. Например:
. 178 345

_____ "218

~29Т ~ТЗТ

600 "283 ~32Т 710 ~345 -275-

600 "283 -42Т

Особенно трудны случаи, при решении которых: 1) переход через разряд происходит в двух разрядах; 2) получается нуль в одном из разрядов; 3) содержится нуль в уменьшаемом; 4) в середине уменьшаемого стоит единица. Например:

375 228

"-"• з •? к КПП

375 + 228

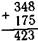546 ~287 ~36Т

710 710

~345 ~345

—^ту^- —тге- или

Нередко при вычитании можно встретить и такую ошибку: вместо того чтобы «занять» единицу высшего разряда, раздробить ее, ученик начинает вычитать из большей цифры вычитаемого меньшую цифру соответствующего разряда уменьшаемого. Например:"

375 529

^___ 8 ~145

373 424

При этом рассуждение проводится так: «Из 5 единиц 8 единиц вычесть нельзя, вычитаем из 8 единиц 5, 7 десятков и 3 сотни

сносим, разность 373».

Учитывая трудности изучения данной темы, необходимо повто­рить с учащимися сложение и вычитание с переходом через раз­ряд в пределах 20 и 100, обратить внимание на решение приме­ров, в которых компонентом является нуль, или нуль получается

в одном из разрядов суммы или __________ ,_______ _{:_____________}

разности (17+3, 25+15, 36-6, 36—27), или нуль содержится в одном из разрядов уменьшаемого или вычитаемого (60—45, 75—40).

I

Тем учащимся, которые долгое время не усваивают запис! примеров в столбик, можно разрешить записывать их в разряди) сетку.

При решении примеров на сложение и вычитание с переходе через разряд соблюдается следующая последовательность:

1) сложение и вычитание с переходом через разряд в одно разряде (единиц или десятков):

278 413

278 351

375 "184

278 14

375 "146

Например:
		.1010
~375	~375	~805	~805	~1000
				148
~229"	Г39~	~Т68~

Особого внимания заслуживает решение примеров вида 800— —236, 810—236, 810—206. Следует сопоставить сначала 1-й и 2-й, а потом 2-й и 3-й примеры, особенности их решения, объ­яснить, в чем их различие, почему получаются разные ответы.

2) сложение и вычитание с переходом через разряд в двуй
разрядах (единиц и десятков): 375+486, 375-186, 286+58, 375-™
-86;

3) особые случаи сложения и вычитания, когда в сумме или в
разности получается один или два нуля, когда в уменьшаемом
содержится один или два нуля, когда в уменьшаемом содержатся
нуль и единица:

4) вычитание трехзначных, двузначных и однозначных чисел из 1000: 1000-375, 1000-75, 1000-5.

При объяснении решения примеров с переходом через разряд, учитывая, что умственно отсталые школьники при сложении забы­вают прибавлять то число, которое надо запомнить, можно разре­шать надписывать это число над соответствующим разрядом.

Например:

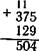+ 375

118

~493~

При вычитании же ставится точка над тем разрядом, из кото­рого заняли единицу. Можно поставить и число 10, которое запи­сывается над разрядом, к единицам которого этот десяток прибав­ляется.

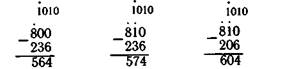
При выполнении действий на сложение и вычитание в преде­лах 1000 решаются примеры с тремя компонентами без скобок и с круглыми скобками: 375+36+124; 379+(542-276); 910-375--264, 375+186-264, 1000-565+136. Решаются также примеры на нахождение неизвестных компонентов действий. Проверка вы­полняется двумя действиями.

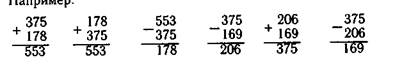
Умножение и деление в пределах 1000

Умножение и деление так же, как сложение и вычитание, могут производиться как устными, так и письменными приемами вычислений, записываться в строчку и столбик.

I. Устное умножение и деление в пределах 1000.

1. Умножение и деление круглых сотен.

Умножение и деление круглых сотен основывается на знании учащимися нумерации, а также табличного умножения и деления. Поэтому, прежде чем знакомить учащихся с умножением и деле­нием круглых сотен, необходимо повторить табличное умножение и деление, а также раздробление сотен в единицы и наоборот. Например: «Сколько содержит 1 сотня единиц? Сколько единиц в 5, 7, 10 сотнях? Сколько сотен составляют 300 единиц? 500 единиц?» И т. д. Объяснение умножения и деления должно сопро-

вождаться операциями с наглядными пособиями и дидактичес|| материалом.

Покажем объяснение умножения, а потом деления.

Например, надо 200-2. Рассуждаем так: 200 — это 2 соТ|
Возьмем 2 сотни палочек и еще 2 сотни палочек. Будет 4 сот!
или 400. Запишем: 2 сот.-2=4 сот.=400, 200-2=400. ?,

При делении 200:2 рассуждаем так: 200 — это 2 сотни. Воз! мем 2 сотни палочек. Если разделить их на две равные части, -т в каждой части получится по одной сотне, или по 100 единим Запишем: 2 сот.:2=1 сот. = 100, 200:2=100. Полезно сопоставим, умножение и деление единиц, десятков и сотен:

ц итков). Делим 18 десятков на 3. Получим 6 десятков, или 60. щишем: 18 дес. :3=6 дес. =60, 180:3=60». Процесс деления ;но показать и на палочках, и на брусках. Сначала учащиеся _г. подробную запись, заменяя единицы десятками, затем запись _!ртывается. От учащихся требуется лишь устное объяснение. [яконец, свертывается и объяснение. Учащиеся записывают лишь

т.

Такое же объяснение проводится и при знакомстве с умноже­нием и делением круглых десятков на однозначное число. Реше­ти- подобных случаев сводится к внетабличному умножению и |и чению. Поэтому приведем лишь подробную запись решения:

3-3= 9

30-3= 90

300-3=900

8:4= 2

80:4= 20

800:4=200

120-4=?

12 дес. -4 дес.=48 дес.=480 120-4=480

480:4=?

48 дес.:4= 12 дес.= 120 480:4=120

3. Умножение и деление трехзначных чисел на однознач­ные без перехода через разряд (123x3, 486:2). Решение таких примеров подготовлено рассмотрением всех предыдущих случаев умножения и деления. Успех выполнения действий здесь зависит от умения учащихся раскладывать числа на разрядные слагаемые. Поэтому предварительно полезны упраж­нения вида 253=200+50+3, 300+60+4=364. Рассуждения проводятся так:

Такая развернутая запись постепенно свертывается: 1) 123-3=369 2) 123-3=369 3) 123-3=369

Рассуждения проводятся устно. Аналогичное свертывание записи происходит и при делении.

Действия умножения и деления надо сопоставлять, проверяя каждое обратным действием: 400x2=800, 800:2=400.

2. Умножение и деление круглых десятков на однозначное число.

а) Рассматриваются случаи умножения и деления круглых де­
сятков, которые сводятся к табличному умножению и делению:
60-3, 180:3. |

б) Рассматриваются случаи, которые сводятся к внетабличному|
умножению и делению без перехода через разряд: 120-3, 480:4.

Перед умножением и делением круглых десятков с учащимися необходимо повторить табличное и внетабличное умножение и деление (4-6, 24-2, 36:6, 36:3), а также определение общего количества десятков в числе («Сколько всего десятков в числе 120, 180, 360, 720?») и количества единиц в десятках («7 десят­ков. Сколько это единиц?»; «Сколько единиц з 2 десятках? 5 де­сятках? 10 десятках? 52 десятках?»).

При объяснении проводятся следующие рассуждения: «60-3=? 60 — это 6 десятков, 6 дес.-3=18 дес. 18 десятков — это 180, значит, 60-3=180». Можно показать учащимся на брусках ариф­метического ящика, пучках палочек, связанных десятками, что результат будет тот же. Для этого учитель берет по 6 брусков 3 раза. Получает 18 брусков, или 18 десятков. Это число 180.

При знакомстве с делением ход рассуждения аналогичен: «180:3=? Узнаем, сколько десятков содержится в числе 180 (18 200

123-3=?_________

123 = 100+20+3 100-3=300 20-3= 60 3-3= 9 300+60+9=369

123=100+20+3 100-3=300 20-3= 60 3-3= 9 300+60+9=369

486:2 = ?________

486=400+80+6 400:2=200 80:2= 40 6:2= 3 200+40+3=243

100-3=300 20-3= 60 3-3= 9 300+60+9=369

4. Умножение 10 и 100, умножение на 10 и 100.

В пределах 1000 рассматривается умножение однозначного двузначного числа на 10 и 100 и соответствующие случаи дел* ния:

8-100=800

8- 10= 80

80- 10=800

10- 3	3- 10	80: 10
100- 8	8-100	800:100
25-100	Ю- 25	250: 10

Умножение числа 10 учитель объясняет, опираясь на понятии умножения как сложения равных чисел.

10-3=10+10+10=30 10-3=30

10-5=10+10+10+10+10=50 10-5=50

Рассматривается еще несколько примеров. Сравниваются отве ты. Учащиеся убеждаются, что при умножении числа 10 на любой множитель к нему справа приписывается нуль.

Затем решаются примеры на умножение однозначного числа ня 10. Решение примера 3x10=? также производится приемом заме ны умножения сложением одинаковых слагаемых:

3-10=3+3+3. . .+3=30 10 раз

1 Можно использовать и переместительный закон умножения: \

10-3=30 3-10=30

Рассмотрев ряд таких примеров, сопоставив произведения и первый множитель, учащиеся приходят к выводу: чтобы умножить число на 10, нужно к первому множителю приписать справа один нуль.

Это правило умножения числа на 10 распространяется и на умножение двузначных чисел (25x10=250).

При умножении на 100 множитель 100 рассматривается как произведение двух чисел: 100=10* 10. Учащиеся практически зна­комятся с использованием сочетательного закона умножения, хотя этот закон они не называют и не формулируют. Учитель объясня­ет: «Чтобы число умножить на 100, его нужно умножить сначала на 10, .. потом произведение умножить еще раз на 10, так как 100=10.10».

Затем запись дается в строчку: 6-100=6-10 • 10=600.

Решается также подробно еще несколько примеров. При реше-«и каждого примера учитель просит сравнивать произведение и !рвый множитель. Учащиеся самостоятельно приходят к выводу: •обы умножить число на 100, к нему нужно приписать справа а нуля.

Умножение 100 на однозначное число выполняется путем ис-

пьзования переместительного закона умножения:

100x5=?

5x100=500

5. Целение на 10 и 100.

Деление на 10, как показывает опыт, лучше усваивается уча­щимися при сопоставлении с действием умножения. Деление на 10 рассматривается как деление по содержанию:

2-10=20, отсюда 20:10=2.

20:10=2 сопровождается вопросом: «Сколько раз в двух десят­ках содержится один десяток?»

Как и в умножении, решается несколько примеров на деление на 10, сравниваются частное и делимое. Учащиеся убеждаются, [• что в частном получается делимое без одного нуля, и делают вывод:

чтобы разделить число на 10, в нем надо отбросить нуль спра­ва. Этот вывод распространяется и на деление круглых сотен и десятков на 10 (400:10=40, 250:10=25).

Аналогично учащиеся знакомятся с делением на 100: 400:100=? 4-100=400 400:100=4

Деление на 100 можно объяснить и последовательным делени­ем на 10 и еще раз на 10:

400:100= 4 400: 10=40 40: 10= 4

400:100=400:10:10=4

Деление на 10 и 100 учащиеся учатся производить как без остатка, так и с остатком: 40:10=4, 45:10=4 (ост. 5).

Следует указать, что при делении числа на 10 (100) опредв ется, сколько всего десятков (сотен) содержится в нем. Учите, необходимо помнить о том, что умственно отсталые школьникь трудом дифференцируют сходные и противоположные понят|| Поэтому, когда ученики познакомились с правилами умножена деления числа на 10, 100, необходимо рассмотреть случаи, | которых эти правила используются одновременно, попросить щихся сравнить их, найти сходство и различие:

4- 10 4-100

10-4 100-4

40:4 400:4

40: 10 400: 10 400:100

Необходимо также сравнить умножение на 10 и 100 с умнонв
нием на 1 и 0, деление на 10, 100 с делением на 1. Это позвол!
каждый раз анализировать выражения, прежде чем приступать!
выполнению действия. ••

Закреплению действия способствует также кратное сравнение! чисел (во сколько раз одно число больше или меньше другого).; Например, даются такие задания: «Во сколько раз 2 меньше, чем/ 20, 200?»; «Во сколько раз 300 больше, чем 3, 10, 100?» Пример 300:3=100 можно прочитать так: «Число 300 больше, чем 3, в 100 раз». Или: «Число 3 меньше, чем 300, в 100 раз». «Какими действиями можно сравнить числа 400 и 10?» — спрашивает учитель. Ученики отвечают: «Сравнить эти числа можно действия­ми деления и вычитания: 400:10, 400—10». Учащиеся учатся самостоятельно ставить вопросы: «На сколько число 400 больше 10?»; «Во сколько раз 400 больше 10?»

II. Письменное умножение и деление в преде­лах 1000.