Приближение функций с помощью метода наименьших квадратов

Пусть в результате изменений в процессе опыта получена таблица некоторой зависимости f:

x	x1	x2	….	xn
f(x)	y1	y2	….	yn

Нужно найти формулу, выражающую эту зависимость аналитически. То есть найти функцию заданного вида y=F(x) (*), которая в точках x₁, x₂, …, x_n принимает значения как можно ближе к табличным значениям y₁, y₂, …, y_n.

Практический вид приближающей функции F можно определить следующим образом. По таблице строится точечный график функции f, а затем проводится кривая по возможности наилучшим образом приближающая характер расположения точек.

По полученной таким образом кривой устанавливается вид приближающей функции. Формула (*) называется уравнением регрессии y на x.

Рассмотрим один из распространенных способов нахождения формулы (*). Предположим, что приближающая функция F в точках x₁, x₂, …, x_n имеет значение y₁*, y₂*, …, y_n* (**). Требование близости табличных значений y₁, y₂, …, y_n и значений y₁*, y₂*, …, y_n* можно истолковать следующим образом. Будем рассматривать совокупность точек таблицы и (**) как координаты двух точек n-мерного пространства М и M*. Задачу формируем таким образом: найти такую функцию F заданного вида, чтобы расстояние между точками M(y₁, …, y_n) и M*(y₁*, …, y_n*) было наименьшим, .т.е

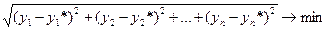
что равносильно

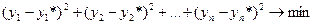
Эта задача носит название приближения функции методом наименьших квадратов.

В качестве приближающих функций в зависимости от характера точечного графика функции f часто используют следующие функции:

1.

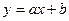
2.

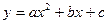
3.

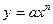
4.

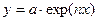
5.

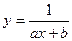
6.

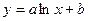
7.

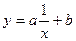
8.

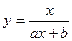
Здесь a, b, c – параметры

Когда вид приближающей функции установлен, задача сводится только к отысканию значений параметров.

Рассмотрим метод нахождения параметров приближающей функции в общем виде на примере приближающих функции с тремя параметрами:

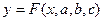
Имеем

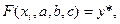i=1, …, n

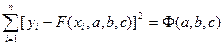
Найдем параметры. Используем необходимое условие экстремума.

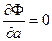
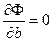
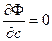
То есть

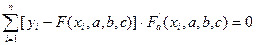
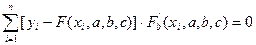
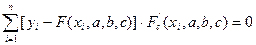
Решив эту систему 3 уравнений с 3 неизвестными относительно параметров a, b, c, мы получим конкретный вид функции F(x,a,b,c).

Естественно ожидать, что значения найденной функции F(x) в точках x₁, x₂, …, x_n будут отличаться от табличных значений y₁, y₂, …, y_n. Значения разностей y_i-F(x_i,a,b,c)= 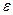_i называются отклонениями эмпирической формулы 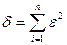должно быть наименьшей.

2.6.2. Нахождение приближающей функции в виде линейной функции и квадратного трехчлена (линейная и квадратичная регрессии)

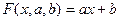
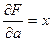
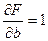
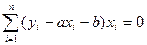
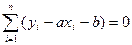
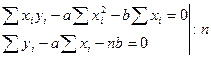
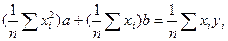
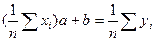
Введем обозначения:

(*)

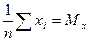
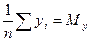
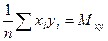
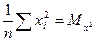
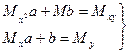Решив систему получим значения параметров a и b, следовательно конкретный вид линейной функции.

В случае нахождения приближающей функции в виде квадратного трехчлена:

(**)

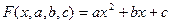
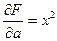
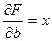
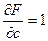
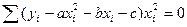
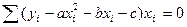
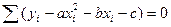
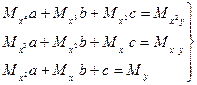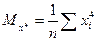
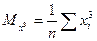
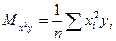
Решение системы (**) дает значение параметров a, b, c для корректной квадратичной функции. Аналогично могут быть найдены функции в виде других элементарных функций.

3.1. Статистические встроенные функции MathCAD

Среднее значение выборки _N-1

mean(v) = 1/N å v_i

ⁱ⁼⁰

Выборочная дисперсия _N-1

var(v) = 1/N å (v_i - mean(v))²

ⁱ⁼⁰

Среднее квадратическое отклонение

stdev(v) = [var(v)]^1/2

Гистограмма hist

hist(array1,array2)

Первый аргумент функции array1 - массив, задающий пределы интервалов,

array2 - массив, содержащий данные выборки.

Результатом функции является массив частот, определяющих, сколько значений массива array2 - содержится в каждом из интервалов.

Коэффициенты корреляции и регрессии

Коэффициент корреляции - corr(vx,vy) (формула для определения была приведена в предыдущей лекции). Аргументами функций д.б. два массива одинаковой длины, задающие координаты точек: вектор vx задает X-координаты точек, вектор vy - Y-координаты точек.

Угловой коэффициент уравнения линейной регрессии - slope(vx,vy),

intercept(vx,vy) - значение Y- координаты точки пересечения графика уравнения линейной регрессии с осью OY.

Вычисление указанных коэффициентов основано на методе наименьших квадратов. Итак, уравнение линейной регрессии имеет вид:

y = ax + b, где a = slope(vx,vy), b = intercept(vx,vy).