Решение систем линейных уравнений
Одной из областью применения матриц является решение систем линейных уравнений.
Системы линейных уравнений можно решить разными способами:
- с помощью обратной матрицы;
- с помощью блока Given – Find.
Решение системы уравнений с помощью обратной матрицы заключается в следующем:
- система уравнений записывается в матричном виде. Для этого нужно составить матрицу коэффициентов, вектор неизвестных и вектор правых частей.
- Чтобы выразить вектор решений, умножим слева обе части уравнения на матрицу, обратную матрице коэффициентов.
- В итоге решение системы уравнений сводится к формуле X=VK-1∙VP,
где: X – вектор неизвестных; VK – вектор коэффициентов; VP – вектор правых частей.
Задание 2.17. Для ознакомления с методами решения систем линейных уравнений выполните листинг 2.16.
Листинг 2.16. Метод решения системы линейных уравнений с помощью обратной матрицы

Решение системы уравнений с помощью блока Given – Find заключается в следующем:
- Наберите вводное слово Given.
- Под вводным словом задайте систему уравнений (можно задавать уравнения и не в матричном виде).
- В качестве знаков равенства следует использовать логическое равенство.
- Задайте произвольные начальные значения для вектора неизвестных значений.
- Введите функцию решения систем уравнений find(xl,x2,...). В скобках через запятую задайте переменные в том порядке, в котором должны быть расположены в ответе соответствующие им корни.
- Поставьте знак числового или символьного вычисления.
Задание 2.18. Для ознакомления с методами решения систем линейных уравнений выполните листинг 2.17.
Листинг 2.17. Метод решения системы линейных уравнений с помощью блока Given – Find.

Задание 2.19. Выполните индивидуальное задание к лабораторной работе в соответствии с номером варианта.
Решите систему уравнений с помощью обратной матрицы и с помощью блока Given – Find
| Номер по варианту | Задание | Фамилия |
| | 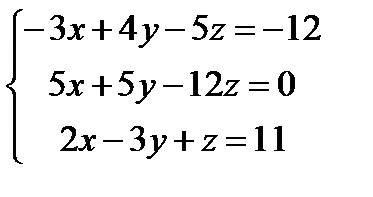 | |
| | 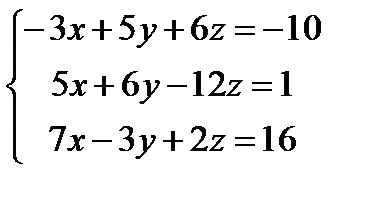 | |
| | 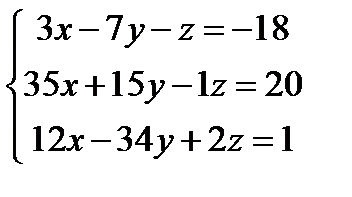 | |
| | 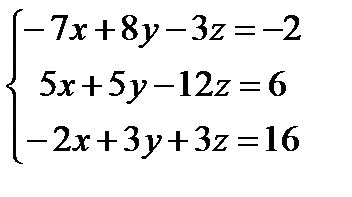 | |
| | 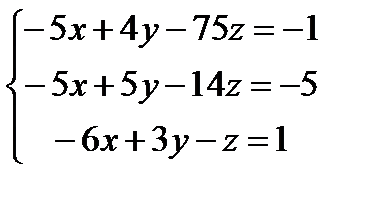 | |
| | 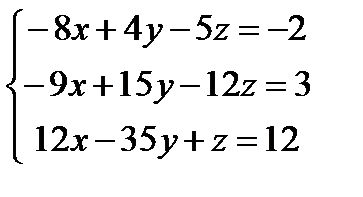 | |
| | 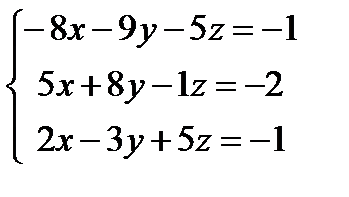 | |
| | 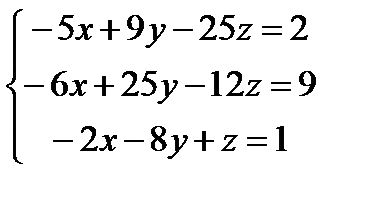 | |
| | 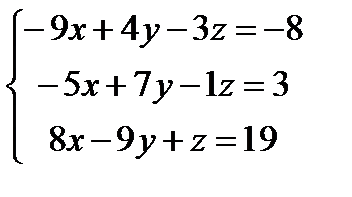 | |
| | 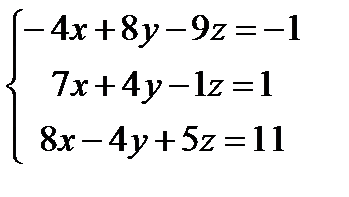 | |
| | 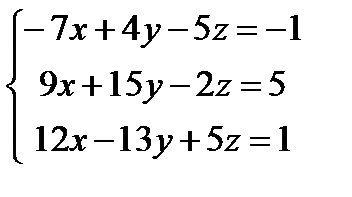 | |
| | 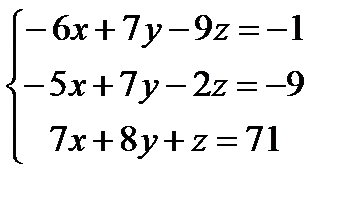 | |
| | 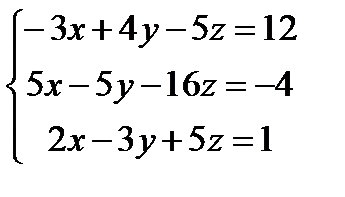 | |
| | 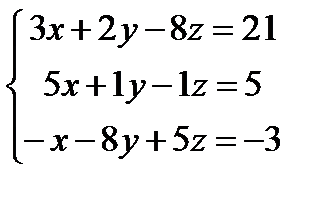 | |
| | 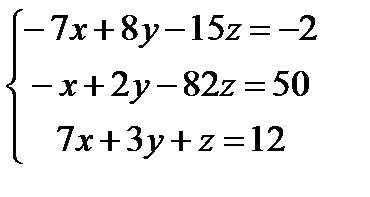 |
Даны две матрицы A и B. Выполните задание согласно варианту.
| Номер по варианту | Задание | Фамилия |
| | 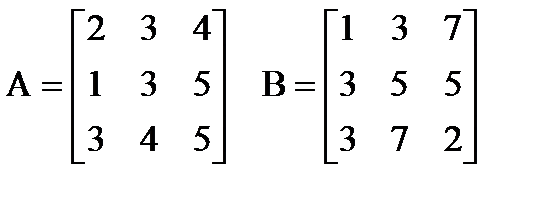 Вычислить: (A∙B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A∙B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей строки матрицы B. | |
| | 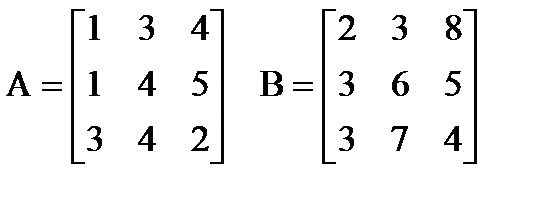 Вычислить: (A∙B)T∙(A-B). Создать вектор V1 из первого столбца матрицы A и вектор V2 из второй строки матрицы B. Вычислить: (A∙B)T∙(A-B). Создать вектор V1 из первого столбца матрицы A и вектор V2 из второй строки матрицы B. | |
| | 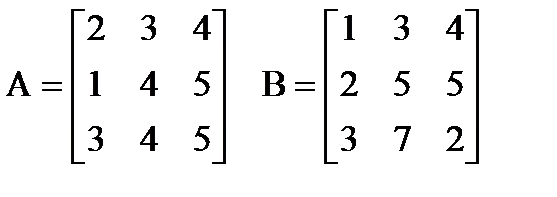 Вычислить: (A+B)∙(A-B)T. Создать вектор V1 из второй строки матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A+B)∙(A-B)T. Создать вектор V1 из второй строки матрицы A и вектор V2 из третьей строки матрицы B. | |
| | 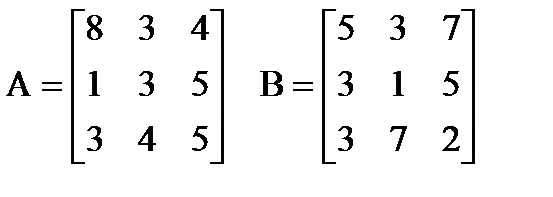 Вычислить: (A+B)∙(A-B)T. Создать вектор V1 из третьего столбца матрицы A и вектор V2 из первой строки матрицы B. Вычислить: (A+B)∙(A-B)T. Создать вектор V1 из третьего столбца матрицы A и вектор V2 из первой строки матрицы B. | |
| | 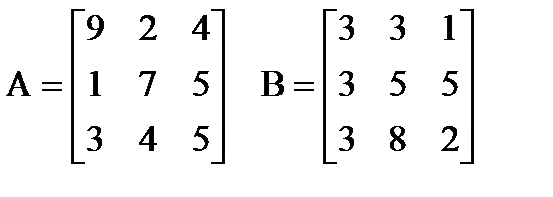 Вычислить: (A∙B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A∙B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей строки матрицы B. | |
| | 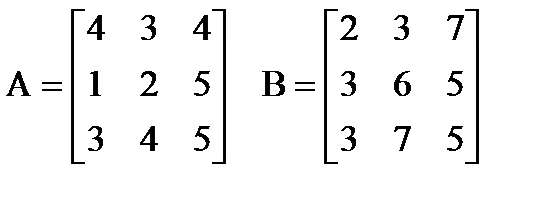 Вычислить: (A+B)∙(A-B)T. Создать вектор V1 из третьего столбца матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A+B)∙(A-B)T. Создать вектор V1 из третьего столбца матрицы A и вектор V2 из третьей строки матрицы B. | |
| | 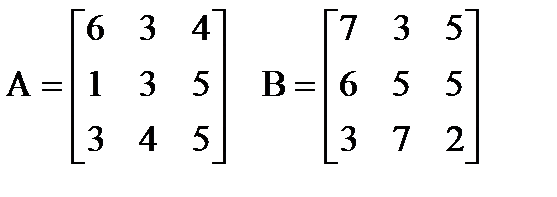 Вычислить: (AT∙B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй строки матрицы B. Вычислить: (AT∙B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй строки матрицы B. | |
| | 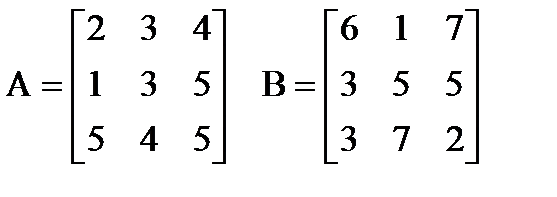 Вычислить: (A-B)∙(A+B)T. Создать вектор V1 из первого столбца матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A-B)∙(A+B)T. Создать вектор V1 из первого столбца матрицы A и вектор V2 из третьей строки матрицы B. | |
| | 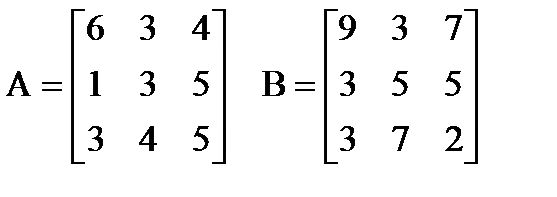 Вычислить: (A∙BT)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей стоки матрицы B. Вычислить: (A∙BT)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей стоки матрицы B. | |
| | 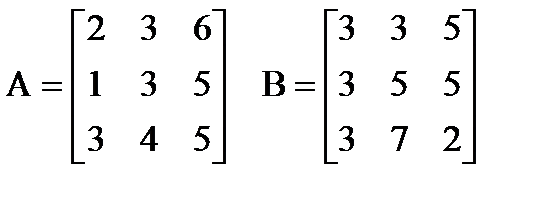 Вычислить: (A∙B)T+(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из первой строки матрицы B. Вычислить: (A∙B)T+(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из первой строки матрицы B. | |
| | 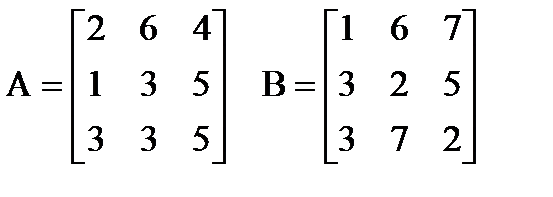 Вычислить: (A∙B)T∙(AT+B). Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй строки матрицы B. Вычислить: (A∙B)T∙(AT+B). Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй строки матрицы B. | |
| | 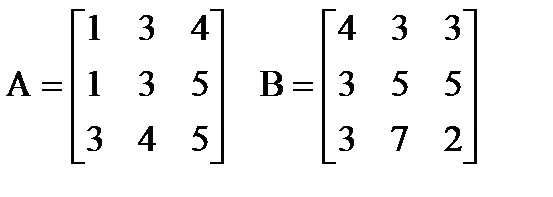 Вычислить: (A∙B)+(A+B)T. Создать вектор V1 из первого столбца матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A∙B)+(A+B)T. Создать вектор V1 из первого столбца матрицы A и вектор V2 из третьей строки матрицы B. | |
| | 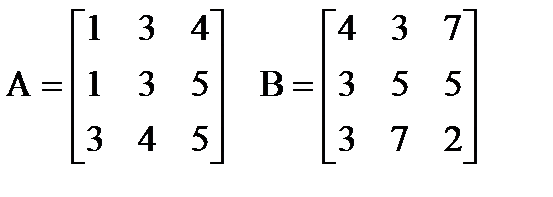 Вычислить: (A-B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй строки матрицы B. Вычислить: (A-B)∙(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй строки матрицы B. | |
| | 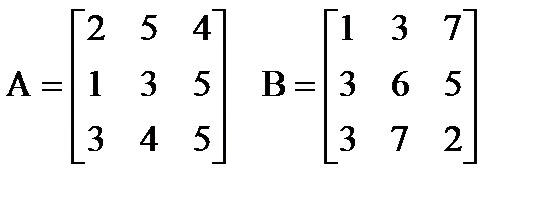 Вычислить: (A∙B)∙(A-B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй стоки матрицы B. Вычислить: (A∙B)∙(A-B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из второй стоки матрицы B. | |
| | 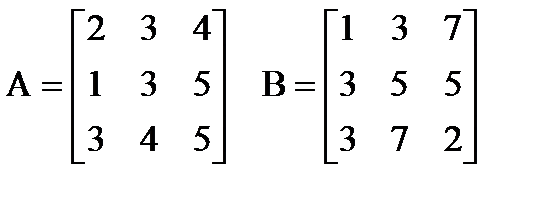 Вычислить: (A∙BT)+(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей строки матрицы B. Вычислить: (A∙BT)+(A+B)T. Создать вектор V1 из второго столбца матрицы A и вектор V2 из третьей строки матрицы B. |
Контрольные вопросы
1. Массив. Реализация массивов в Mathcad.
2. Вектор. Матрица. Тензор.
3. Способы задания массивов.
4. Создание массива командой Вставка Матрицы.
5. Обращение к отдельным переменным.
6. Организация индексации в массивах.
7. Изменение стартового индекса в массиве.
8. Создание массива определением его отдельных элементов.
9. Создание тензора.
10. Объявление ранжированных переменных.
11. Вкладка матричных операций Матрица.
12. Элементарные операции над матрицами и скаляром.
13. Сложение и вычитание матриц.
14. Умножение матриц между собой.
15. Транспонирование матрицы.
16. Определитель матрицы.
17. Обратная матрица.
18. Функции определения размерности массивов.
19. Функции сортировки массивов.
20. Функции выделения и слияния массивов.
21. Решение систем уравнений с помощью обратной матрицы.
22. Решение систем уравнений с помощью блока Given – Find.
