Создание массива определением его отдельных элементов

Массив можно определить, присваивая значения непосредственно отдельным элементам массива.

Способ позволяет присвоить нужное значение как всем элементам массива (см. листинг 2.5), так и части из них, либо даже одному единственному элементу. В последнем случае создается массив, размерность которого задается индексами введенного элемента (листинг 2.5), а неопределенным элементам по умолчанию присваиваются нулевые значения.

В любом месте документа допускается как переопределение любого из элементов массива (листинг 2.5), так и изменение его размерности. Чтобы поменять размерность всего массива, просто присвойте любое значение новому элементу, индексы которого выходят за границы прежней размерности (листинг 2.5).

В местозаполнители элементов матрицы допускается вставка любых функций, подобно применению обычного оператора присваивания.

Задание 2.6. Для ознакомления с определением отдельных элементов массивов выполните листинг 2.5.

Листинг 2.5. Создание массива определением отдельных элементов

Создание тензора

Определение отдельных элементов – удобный способ создания тензоров (многоиндексных массивов). В Mathcad имеется непосредственная возможность работы только с векторами и матрицами. Тем не менее, можно создать тензор путем определения вложенного массива. Для этого необходимо присвоить каждому элементу матрицы значение в виде другого вектора или матрицы (листинг 2.6). Пользователь должен лишь позаботиться о корректности задания индексов тензора и не запутаться в индексировании вложенных матриц.

Задание 2.7. Для ознакомления с работой тензоров выполните листинг 2.6.

Листинг 2.6. Создание тензора и доступ к его элементам

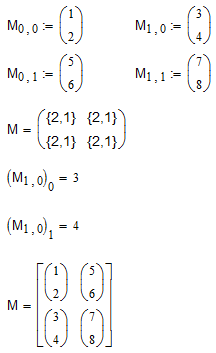
Обратите внимание, что Mathcad по умолчанию не отображает трехмерную структуру тензора ( листинг 2.6), а вместо этого показывает информацию о размерах каждого элемента матрицы.

Развернуть вложенные массивы можно с помощью команды Формат / Результат / Параметры отображения (Format / Result / Display Options), устанавливая флажок Разворачивать вложенные массивы (Expand Nested Arrays) на вкладке Параметры отображения (Display Options).

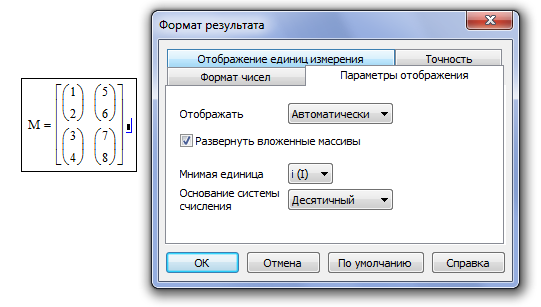
Рисунок 2.3. – Разворачивание вложенных массивов.

Ранжированные переменные

Ранжированные переменные в Mathcad являются разновидностью векторов и предназначены, главным образом, для создания циклов или итерационных вычислений. Простейший пример ранжированной переменной – это массив с числами, лежащими в некотором диапазоне с некоторым шагом.

Например, для создания ранжированной переменной s с элементами 0,1,2,3,4,5:

Поместите курсор ввода в нужное место документа.

Введите имя переменной (s) и оператор присваивания ":".

Нажмите кнопку Ранжированная переменная (Range Variable) на панели Матрица (Matrix), показанную на рис. 2.4, либо введите символ точки с запятой с клавиатуры.

В появившиеся местозаполнители (рисунок. 2.4) введите левую и правую границы диапазона изменения ранжированной переменной 0 и 5.

Рисунок 2.4. – Создание ранжированной переменной.

Результат создания ранжированной переменной показан на рисунке 2.5.

Рисунок 2.5. – Вывод ранжированной переменной.

Чтобы создать ранжированную переменную с шагом, не равным 1, например, 0,2,4,6,8:

Создайте ранжированную переменную в диапазоне от 0 до 8 (см. рисунок 2.6).

Поместите линии ввода на значение начала диапазона (0).

Введите запятую.

В появившийся местозаполнитель (рисунок 2.6) введите значение шага изменения ранжированной переменной (2).

Созданная ранжированная переменная будет иметь значения от 0 до 8 включительно, с шагом, равным 2.

Рис. 2.6. Вывод ранжированной переменной

Задание 2.8. Для ознакомления с работой ранжированных переменных выполните листинг 2.7.

Листинг 2.7. Применение ранжированных переменных

Матричные операции

Доступ к некоторым операциям для матриц осуществляется с помощью панели Матрица (Matrix). На рисунке 2.6 приведены описание кнопок панели Матрица.

Рисунок 2.6. – Инструменты панели Матрица.

В Mathcad к матрице можно прибавлять (или отнимать от нее) любое число. При этом оно будет прибавлено ко всем (или вычтено из всех) элементов исходной матрицы.

При умножении матрицы на скаляр на него умножается каждый элемент исходной матрицы. Аналогично умножению, матрицу можно разделить на скаляр. Во всех операциях матрица и скаляр могут быть представлены и символически: как в виде буквы, так и в виде выражения.

Задание 2.9. Для ознакомления с элементарными операциями над матрицами и скаляром выполните листинг 2.8.

Листинг 2.8. Элементарные операции над матрицами и скаляром

Чтобы сложить или вычесть матрицы, используются привычные символы "+" или "–" которые помещаются между соответствующими матрицами.

При этом к каждому элементу М первой матрицы прибавится (или вычтется из него) элемент М1 второй матрицы. Результатом будет третья матрица, элементы которой являются суммой (разностью) соответствующих элементов суммируемых (вычитаемых) матриц. Естественно, матрицы должны быть одинаковой размерности, иначе будет выдано сообщение об ошибке. Кроме того, в выражениях матричного сложения или вычитания можно использовать и коэффициенты.

Задание 2.10. Для ознакомления с операциями сложения, вычитания и умножения матриц выполните листинг 2.9.

Листинг 2.9. Элементарные операции над матрицами

Система Mathcad позволяет проводить операции возведения матрицы в степень. Если матрица квадратная, ее можно возвести в степень n, где n – любое целое число (или 0).

При этом выполняются следующие правила:

если n=0, т о (по аналогии с традиционной алгеброй) М⁰ =Е, где Е – единичная матрица;

если n=1, то М¹ =М (матрица, возведенная в первую степень, равна сама себе);

если n=N, где N – любое натуральное число, равное или большее 2, то степень матрицы определяется как произведение соответствующего числа матриц в первой степени. Подобное произведение возможно, поскольку при перемножении две квадратные матрицы равной размерности дают третью с той же размерностью;

если n=-1, то М^-1 – это матрица, обратная данной матрице;

если n=R, где R – любое целое отрицательное число, меньшее либо равное -2, то аналогично возведению в положительную степень, M^R определяется как произведение нужного числа обратных матриц.

Задание 2.11. Для ознакомления с операциями возведения матрицы в степень выполните листинг 2.10.

Листинг 2.10. Возведение матрицы в степень

Одной из распространённых операций над массивами является транспонирование. Транспонированием называется матричная операция, переводящая матрицу размерности MxN в матрицу размерности NxM. Т.е. при транспонировании строки исходной матрицы превращаются в столбцы, а столбцы – в строки. Оператор транспонирования (Transpose) находится на панели Матрица (Matrix).

Следующая операция для матриц это вычисление определителя матрицы. Определитель – это число (или выражение), которое прежде всего характеризует линейную независимость строк (или столбцов) матрицы.

Обратная матрица – Матрица А^-1 называется обратной к матрице А, если выполняется условие А∙А^-1=Е. Где Е – единичная матрица, (матрица у которой элементы главной диагонали равны 1, а все остальные – 0). Матрица имеет обратную только в том случае, если она квадратная и ее определитель не равен 0.

В некоторых случаях приходится находить сумму элементов вектора. Для этого в Mathcad существует специальный оператор Сумма вектора (Vector Sum), который расположен на панели Матрица (Matrix).

Задание 2.12. Для ознакомления с операциями над матрицами выполните листинг 2.11.

Листинг 2.11. Возведение матрицы в степень