Раздел 4. Словарь терминов (глоссарий).

Событиемназывается всякий факт, который может произойти или не произойти в результате опыта.

Достоверным событиемназывается событие, которое наверняка произойдет в результате опыта. Событие называется невозможным, если оно никогда не произойдет в результате опыта.

Полной группой событий называется совокупность всех возможных результатов опыта.

Элементарными исходами опыта называются такие результаты опыта, которые взаимно исключают друг друга и в результате опыта происходит одно из этих событий, также каково бы ни было событие А, по наступившему элементарному исходу можно судить о том, происходит или не происходит это событие.

Совокупность всех элементарных исходов опыта называется пространством элементарных событий.

События называются равновозможными, если нет оснований считать, что одно из них появится в результате опыта с большей возможностью.

События называются несовместными, если появление одного из них исключает появление других.

Вероятностью события А называется математическая оценка возможности появления этого события в результате опыта. Вероятность события А равна отношению числа благоприятствующих событию А исходов опыта к общему числу попарно несовместных исходов опыта, образующих полную группу событий.

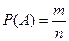
Исход опыта является благоприятствующим событию А, если появление в результате опыта этого исхода влечет за собой появление события А.

Относительной частотой события А называется отношение числа опытов, в результате которых произошло событие А к общему числу опытов.

Статистической вероятностьюсобытия А наз. относительную частоту этого события .

Геометрические вероятности - вероятности попадания точки в какой – либо отрезок или часть плоскости (пространства).

Так если на отрезке длиной L выделен отрезок длины l, то вероятность попадания наугад взятой точки в отрезок l равна отношению l/L.

События А и В называются равными, если осуществление события А влечет за собой осуществление события В и наоборот.

Суммой событий А_k называется событие A, которое означает появление хотя бы одногоиз событий А_k.

Произведениемсобытий A_k называется событие А, которое заключается в осуществлении всех событий A_k.

Разностью событий А и В называется событие С, которое означает, что происходит событие А, но не происходит событие В.

Противоположнымк событию А называется событие 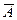,означающее,что событие А не происходит.

Событие А называется независимым от события В, если вероятность события А не зависит от того, произошло событие В или нет. Событие А называется зависимым от события В, если вероятность события А меняется в зависимости от того, произошло

событие В или нет.

Вероятность события В, вычисленная при условии, что имело место событие А, называется условной вероятностью события В.

Если производится некоторое количество испытаний, в результате которых может произойти или не произойти событие А, и вероятность появления этого события в каждом из испытаний не зависит от результатов остальных испытаний, то такие испытания называются независимыми относительно события А.

Случайной величинойназывается величина, которая в результате опыта может принимать то или иное значение, причем заранее не известно какое именно.

Дискретной случайной величиной называется такая величина, которая в результате опыта может принимать определенные значения с определенной вероятностью, образующие счетное множество (множество, элементы которого могут быть занумерованы).

Непрерывной случайной величиной называется такая величина, которая может принимать любые значения из некоторого конечного или бесконечного промежутка.

Соотношение между возможными значениями случайной величины и их вероятностями называется законом распределения дискретнойслучайной величины.

Закон распределения может быть задан аналитически, в виде таблицы или графически.

Таблица соответствия значений случайной величины и их вероятностей называется рядом распределения.

Графическое представление этой таблицы называется многоугольником распределения. При этом сумма все ординат многоугольника распределения представляет собой вероятность всех возможных значений случайной величины, а, следовательно, равна единице.

Числовыми характеристиками случайной величины называются величины , которые определяют некоторое среднее значение, вокруг которого группируются значения случайной величины, и степень их разбросанности вокруг этого среднего значения.

Математическим ожиданием дискретной случайной величины называется сумма произведений всех возможных значений случайной величины на их вероятности.

Математическое ожидание существует, если ряд, стоящий в правой части равенства, сходится абсолютно. Математическое ожидание приближенно равно среднему арифметическому наблюдаемых значений случайной величины.

Дисперсией (рассеиванием) дискретной случайной величины называется математическое ожидание квадрата отклонения случайной величины от ее математического ожидания.

Средним квадратическим отклонениемслучайной величины Х называется квадратный корень из дисперсии

Функцией распределения называют функцию F(x), определяющую вероятность того, что случайная величина Х в результате испытания примет значение, меньшее х.

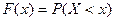
Функцию распределения также называют интегральной функцией.

Функция распределения существует как для непрерывных, так и для дискретных случайных величин. Она полностью характеризует случайную величину и является одной из форм закона распределения.

Для дискретной случайной величины функция распределения имеет вид:

Знак неравенства под знаком суммы показывает, что суммирование распространяется на те возможные значения случайной величины, которые меньше аргумента х.

Функция распределения дискретной случайной величины Х разрывна и возрастает скачками при переходе через каждое значение х_i.

Плотностью распределения вероятностей непрерывной случайной величины Х называется функция f(x) – первая производная от функции распределения F(x).

Плотность распределения также называют дифференциальной функцией. Для описания дискретной случайной величины плотность распределения неприемлема.

После введения функций распределения и плотности распределения можно дать следующее определение непрерывной случайной величины.

Случайная величина Х называется непрерывной, если ее функция распределения F(x) непрерывна на всей оси ОХ, а плотность распределения f(x) существует везде, за исключением, может быть, конечного числа точек.

Математическим ожиданиемнепрерывной случайной величины Х, возможные значения которой принадлежат отрезку [a,b], называется определенный интеграл

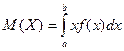
Если возможные значения случайной величины рассматриваются на всей числовой оси, то математическое ожидание находится по формуле:

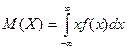
При этом предполагается, что несобственный интеграл сходится.

Дисперсией непрерывной случайной величины называется математическое ожидание квадрата ее отклонения.

По аналогии с дисперсией дискретной случайной величины, для практического вычисления дисперсии используется формула:

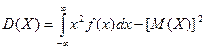
Средним квадратическим отклонениемназывается квадратный корень из дисперсии.

Модой М₀ дискретной случайной величины называется ее наиболее вероятное значение. Для непрерывной случайной величины мода – такое значение случайной величины, при которой плотность распределения имеет максимум.

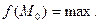
Медианой M_D случайной величины Хназывается такое ее значение, относительно которого равновероятно получение большего или меньшего значения случайной величины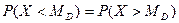

Геометрически медиана – абсцисса точки, в которой площадь, ограниченная кривой распределения делится пополам.

Начальным моментом порядка k случайной величины Х называется математическое ожидание величины Х^k. : 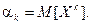Для дискретной случайной величины: . Для непрерывной случайной величины: .

Центральным моментом порядка k случайной величины Х называется математическое ожидание величины :

Для дискретной случайной величины: .

Для непрерывной случайной величины: .

Отношение центрального момента третьего порядка к среднему квадратическому отклонению в третьей степени называется коэффициентом асимметрии.

Для характеристики островершинности и плосковершинности распределения используется величина, называемая эксцессом.

Непрерывная случайная величина имеет равномерноераспределение на отрезке [a, b], если на этом отрезке плотность распределения случайной величины постоянна, а вне него равна нулю :

Показательным (экспоненциальным)называется распределение вероятностей непрерывной случайной величины Х, которое описывается плотностью

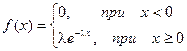
где l - положительное число.

Функцией надежностиR(t) называют функцию, определяющую вероятность безотказной работы устройства в течение времени t.

Функция надежности для какого- либо устройства при показательном законе распределения равна:

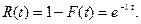
Данное соотношение называют показательным законом надежности.

Нормальнымназывается распределение вероятностей непрерывной случайной величины, которое описывается плотностью вероятности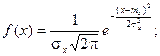

Нормальный закон распределения также называется законом Гаусса.

График плотности нормального распределения называется нормальной кривойили кривой Гаусса.

Функция называется функцией Лапласаили интегралом вероятностей.

Значения этой функции при различных значениях х посчитаны и приводятся в специальных таблицах.

Функцию Лапласа также называют функцией ошибок и обозначают erf x.

Еще используется нормированнаяфункция Лапласа, которая связана с функцией Лапласа соотношением: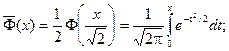

При рассмотрении нормального закона распределения выделяется важный частный случай, известный как правило трех сигм.

,

т.е. вероятность того, что случайная величина отклонится от своего математического ожидание на величину, большую , чем утроенное среднее квадратическое отклонение практически равна нулю.

Законом распределения системы случайных величин называется соотношение, устанавливающее связь между областями возможных значений системы случайных величин и вероятностями появления системы в этих областях.

Функцией распределения системы двух случайных величин называется функция двух аргументов F(x, y), равная вероятности совместного выполнения двух неравенств X<x, Y<y.:

Плотностью совместного распределениявероятностей двумерной случайной величины (X, Y) называется вторая смешанная частная производная от функции распределения :

Математическая статистика – раздел математики, в котором изучаются методы сбора, систематизации и обработки результатов наблюдений массовых случайных явлений для выявления существующих закономерностей

Генеральная совокупность – совокупность всех подлежащих изучению объектов относительно некоторого признака (с.в.) Х.

Выборочная совокупность ( выборка ) – ограниченная совокупность объектов. отобранных случайным образом из генеральной совокупности.

Выборка наз. репрезентативной,если она достаточно хорошопредставляет изучаемый признак Х объектов генеральной совокупности.

Объём генеральной или выборочной совокупности – число объектов (наблюдений) в соответствующей совокупности.

Варианты 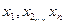– значения изучаемого признака (с.в.) Х.

Ранжирование статистических данных – операция расположения вариант по неубыванию.

Вариационный ряд- последовательность вариант, записанных в неубывающем порядке.

Частота варианты 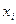- число 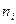, показывающее, сколько раз встречается эта варианта в ряде наблюдений.

Относительная частота варианты - отношение частоты варианты к объёму выборки.

Статистическим распределением выборки называется перечень вариант и соответствующих им частот или относительных частот.

Эмпирической ( выборочной ) функцией распределения называется функция ,

определяемая соотношением

W(X<x).

Полигон частот- ломаная с вершинами в точках ( , ).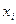

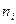Полигон относительных частот - ломаная с вершинами в точках ( . ).

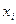Гистограмма частот (относительных частот) - ступенчатая фигура, состоящая из прямоугольников, основаниями которых служат частичные интервалы длины h , а высоты равны плотностям частот 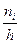( плотностям относительных частот ). Выборочная средняя - среднее арифметическое всех вариант выборки.

Выборочная дисперсия среднее арифметическое квадратов отклонений всех вариант от выборочной средней.

Выборочное среднее квадратическое отклонение (с.к.о.) есть квадратный корень из выборочной дисперсии.

Исправленная выборочная дисперсия. определяется соотношением

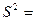
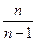
Исправленное выборочное с.к.о. S есть квадратный корень из исправленной выборочной дисперсии.

Размах вариации R - разность между наибольшей и наименьшей вариантами

Мода 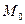вариационного ряда- варианта, имеющая наибольшую частоту.

Медиана 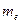- варианта, стоящая в середине вариационного ряда.

Статистикой называют всякую функцию результатов наблюдений, т.е. любую функцию выборки

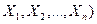
Статистической оценкой 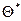неизвестного параметра 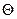теоретического распределения изучаемого признака Х называется статистика 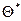, которая в определённом смысле близка к истинному значению .

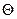Точечная статистическая оценка (т.с.о.)есть стат. оценка 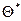, определяемая одним числом.

Т.с.о. 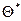называется несмещённой т.с.о. параметра 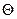, если .

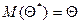В противном случае, т.с.о. 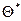называется смещённой т.с.о. параметра .

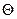Т.с.о. 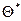параметра 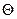называется состоятельной, если она сходится по вероятности к оцениваемому параметру.

Т.с.о. 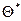параметра 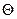называется эффективной, если её дисперсия минимальна.

Оценка неизвестного параметра 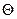называется интервальной, если она

Определяется двумя числами - концами интервала, в котором находится .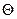

Интервал ( , ), покрывающий с заданной вероятностью истинное

значение параметра 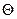, называется доверительным интервалом, а вероятность - надёжностью оценки или доверительной вероятностью.

Случайные величины X и Y называются независимыми, если изменение любой из них не влечёт изменение распределения другой.

Если изменение хотя бы одной из случайных величин X или Y влечёт изменение распределения другой, то зависимость между Х и Y называется

статистической.

Статистическая зависимость, при которой изменение одной с.в. влечёт изменение среднего значения другой с.в. наз. корреляционной.

Условным средним наз. среднее арифметическое значений с.в. Y, соответствующих значению с.в. Х: Х=х

Корреляционной зависимостью с. в. Y от с. в. Х наз. функциональную

зависимость условной средней от х: = f(x).

Соотношение = f(x) наз. уравнением регрессии с.в. Y на с.в. X.

Функцию f(x) наз. функцией регрессии с.в. Y на с.в. X.

График Функции f(x) наз. линией регрессии с.в. Y на с.в. X.

Аналогично определяются уравнение регрессии с.в. X на с.в. Y,

функция g(y) регрессии с.в.. X на с.в. Y, линия регрессии с.в. X на с.в. Y.

Если обе функции регрессии f(x) и g(y) - линейны, то корреляцию наз.

линейной; в противном случае – нелинейной корреляцией.

Уравнения линий регрессии, найденные по результатам выборки, наз.