Расчет оптимальных партий пополнения запасов

На рис. 5 приведена упрощенная схема складской системы. Поток товаров со склада к потребителям непрерывен и характеризуется интенсивностью потребления λ — количеством единиц товара, потребляемых за 1 год.

Поток товаров от источника к складу является дискретным и характеризуется размерами партии (Q) и периодам времени между поставками (T).

Уменьшение затрат на: ведет к увеличению затрат на:

Транспорт

Содержание складских запасов (увеличение запасов, так как закупают большими партиями)

Транспорт (чаще приходится подвозить требуемый товар)

Транспорт (повреждения при транспортировке)

Содержание складских запасов (увеличение запасов, так как завозят реже и, следовательно, большими партиями)

	Упаковку
		Прогнозирование изменений потребительского спроса
		Закупку

Содержание внешних складов запасов (так как их должно быть больше, чтобы своевременно удовлетворять заказы)

	Обработку и своевременное оформление заказов потребителей
		Производство (возможны простои оборудования из-за отсутствия ресурсов)
	Содержание складских запасов

Рис. 3 Примеры конфликта затрат

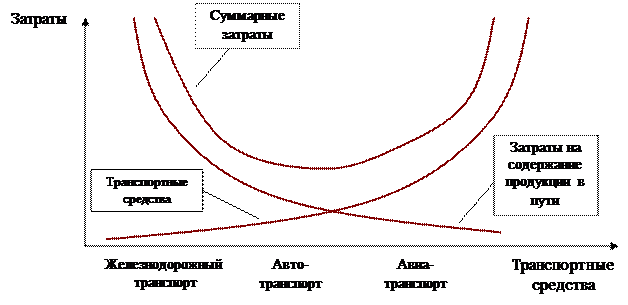
Рис. 4. Пример состыковки конфликтующих затрат

		Источник (производство или центральный склад)
			Склад
	Потребители

Рис. 5 Упрощенная схема складской системы

Формула Уилсона

Формулой Уилсона принято называть формулу для определения оптимального размера партии при мгновенном пополнении запаса и постоянном темпе потребления.

Цикл изменения запасов на складе для этого случая изображен на рис. 6. Абсолютное значение tg а равно интенсивности потребления (λ):

.

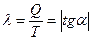Формулу для определения издержек хранения за период Т (С^T_хр) можно вывести следующим образом:

С^T_хр= ic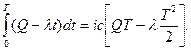

С учетом того, что λ = Q/ Т, получаем:

С^T_хр= icT 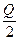. (4)

Рис. 6. Изменение запаса на складе при мгновенном пополнении запаса

Издержки поставки за период Т (C^T_пост ) определяются формулой (1):

C^T_пост =A + C(Q).

Определим среднегодовые суммарные издержки снабжения (С_год). Для упрощения вывода будем считать, что в году целое число продолжительностью Т. В принципе можно обойтись без этого допущения, но тогда вывод значительно усложняется. Если в году целое число циклов, то оно равно 1/Т. Тогда формула определения среднегодовых суммарных издержек имеет вид:

C_год= (С^T_хр+ C^T_пост)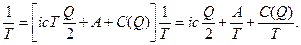

С учетом того, что Т= Q/ λ и с = C(Q)/Q,,

C_год= 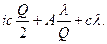(5)

Выведенную выше формулу для определения суммарных годовых издержек снабжения можно получить и путем простых логических рассуждений.

Первое слагаемое в формуле (годовые затраты на хранение запасов) представляет собой затраты на хранение единицы запасов (iс), умноженные на средний уровень запасов в течение года (Q/2). Второе слагаемое — это годовые затраты на заказы партий, вычисляемые как стоимость заказа одной партии (A), умноженная на количество заказов за год( 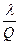). Третье слагаемое — это стоимость приобретенных за год запасов, рассчитанная как средняя стоимость поставки единицы товара (с), умноженная на годовое потребление товара (λ).

Размер оптимальной партии для пополнения запаса (Q*) определяется из условия, что С_год (Q*) → min. Это условие выполняется, ес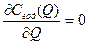ли

или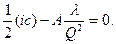

Из этого выражения получим формулу для определения оптимального размера партии для пополнения запаса (Q*), называемую формулой Уилсона:

Q = 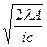(6)

При пополнении запаса партиями размером (Q*) издержки снабжения будут минимальными.

Графическая интерпретация алгоритма определения оптимального размера партии при мгновенном пополнении запаса и постоянном темпе потребления (рис. 7) показывает, что оптимальный размер партии заказа определяется при состыковке затрат на хранение запасов и заказ партий.

Определим точку или уровень заказа (х_заказ), требуемую в решении задачи (рис. 8) - значение запаса на складе, при котором делают заказ на пополнение запаса. Так как заказ должен поступать в момент времени, когда наличный запас на складе равен нулю, то уровень заказа определяется как потребление за время выполнения заказа минус сделанные, но неполученные заказы: х_заказ= 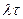при τ ≤ T; х_заказ= 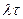-Q^* при T ≤ τ ≤ 2T; х_заказ= 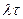-2Q^* при 2T ≤ τ ≤ 3T и т.д.

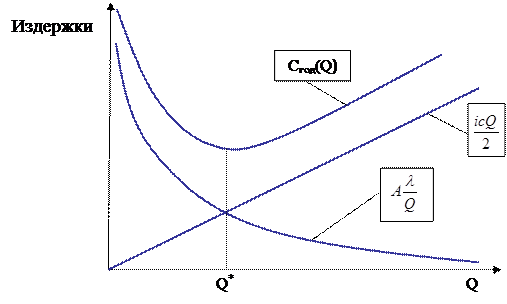
Рис. 7 Состыковка затрат на хранение запасов и заказ партий

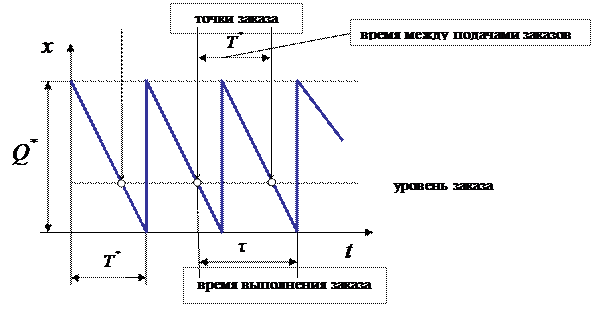
Рис. 8 Определение точки заказа

Задача 4.Интенсивность потребления λ = 600 ед. в год. Стоимость заказа А = 8 долл. Время выполнения заказа τ = 1 год. Средняя стоимость единицы запаса с = 0,3 долл. Коэффициент пропорциональности затрат на хранение i = 0,2. Определить оптимальный размер партии, время между подачами заказов, уровень заказа, минимальные годовые издержки.

Оптимальный размер партии:

Q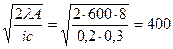^* = ед.

Время между подачами заказов:

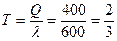г. = 8 мес.

Уровень заказа:

х_заказа= λτ – Q^* = 600 ×1 – 400 = 200 ед.

Минимальные годовые издержки:

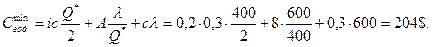
Задача 5.Потребность фирмы в сырье - 2000 ед./год.Затраты по хранению единицы сырья - 5 д.е., затраты по размещениюи исполнению заказа — 60 д.е. Определить: а) оптимальный размер заказа; б) если поставщик отказывается завозить сырье чаще, чем 4 раза в год, какую сумму может заплатить фирма, чтобы снять это ограничение?

Решение. Если поставщик завозит сырье 4 раз/год, то размер партии составляет: 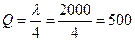ед.

Оптимальный объем партии вычислим по формуле Уилсона:

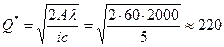ед.

Сокращение затрат при закупке оптимальными партиями составит:

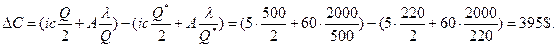
Ответ: Чтобы снять ограничение на период между закупками, фирма может заплатить поставщику не более 395 д.е.