Безразмерная математическая модель системы управления манипулятором.

Полученные выше уравнения движения манипулятора являются размерными, т.е. коэффициенты уравнений имеют определенную физическую размерность и их нельзя сравнивать между собой с целью выяснения, какие из них являются существенными для моделирования процессов в манипуляторы, а какие несущественны и могут быть, например, отброшены для снижения трудностей при решении этих уравнений.

Существует специальная наука - “Теория подобия и размерности” [17 ], которая предписывает, как привести размерные дифференциальные уравнения к безразмерному виду, чтобы можно было сравнивать в уравнениях отдельные члены уравнений и, кроме того, как строить физические модели для проверки правильности принятых решений об отбрасывании некоторых несущественных членов дифференциальных уравнений.

Согласно “Теории подобия и размерности” необходимо выбрать в системе, математическое моделирование которой производится, некоторые, характерные именно для этой системы, параметры, определяющие протекание в системе процессов.

Известно [16], что в гибких стержнях характерные процессы определяются такими параметрами стержней и их материала:

E - модуль упругости материала;

J – момент инерции поперечного сечения стержня;

s – длина стержня;

ρ – плотность материала стержня.

Их этих параметров можно составить комбинацию, имеющую размерность времени . Эта комбинация представляет собой характерное время протекающих в стержнях процессов,

С помощью T можно все процессы в стержне согласовать по времени, введя безразмерное время t = t*/T.

Для приведения различных параметров в дифференциальных уравнениях, имеющих размерность длины, необходимо ввести единые масштабы измерения длин элементов манипулятора. В качестве такой единой линейки выберем самый главный размер, от которого зависит возможность выполнения манипулятором своих рабочих функций. Это будет d - характерный прогиб стержня.

Имея единый масштаб длины можно ввести безразмерные переменные:

y₁= y₁*/δ , y₁ - безразмерное упругое перемещение конца стержня;

y=y^*/d, y – безразмерный прогиб стержня;

z=z^*/s, z – безразмерная координата поперечного сечения стержня.

,

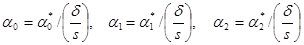
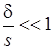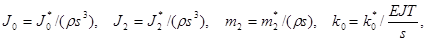
Здесь a₀, a₁, a₂, J₀, J₁, J₂, m₂ , k₀, L₁, L₂, N₂, g – безразмерные значения соответствующих размерных переменных и параметров.

Теперь можно представить уравнения движения манипулятора в безразмерной форме.

Окончательно можно записать:

Обыкновенные дифференциальные уравнения движения абсолютно твердых вала и исполнительного органа.

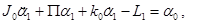(2.8)

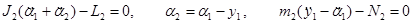(2.9)

Дифференциальное уравнение с частными производными, моделирующее процессы изгиба стержня.

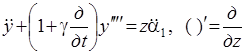(2.10)

Граничные условия.

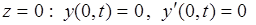(2.11)

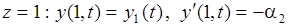
Начальные условия.

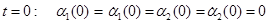(2.12)

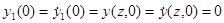
Уравнения связи абсолютно твердых вала и исполнительного органа через гибкий стержень.

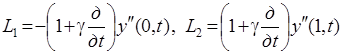(2.13)

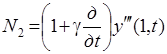
Проведем прямое интегральное преобразование Лапласа и получим уравнения системы управления манипулятором в изображениях

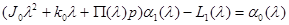, (2.14)

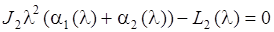, (2.15)

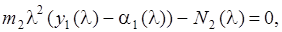(2.16)

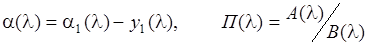
(2.17)

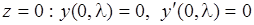(2.18)

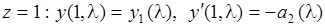
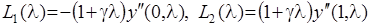(2.19)

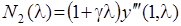
Здесь a₀(l), a₁(l), a₂(l), y₁(l), y(z,l) L₁(l), L₂(l), N₂(l) – изображения соответствующих оригиналов; A(l) и B(l) – многочлены; П(l) – рациональная дробь; l – произвольный комплексный параметр.

Выберем характерный прогиб d стержня, используя методы теории упругости.

Согласно этой теории [1] в стержне будут отсутствовать пластические деформации, если его характерный прогиб d удовлетворяет условию 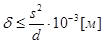; поэтому принимаем 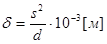,где d - характерный диаметральный размер поперечного сечения стержня в направлении изгиба.