Динамика температуры теплоносителя в реакторе

Обозначим:

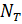- текущая тепловая мощность реактора (активной зоны), определяемая в разделе 2 по ф. 2.1.

t₁₀ – температура на входе в корпус реактора, в данной задаче является задаваемой (независимой) переменной;

t₁₁ – средняя температура во входном объеме реактора (на входе в активную зону);

t₁₂ – температура на середине высоты активной зоны (средняя по объему активной зоны);

t₁₃ – температура на выходе из активной зоны;

t₁₄ – температура в выходном (верхнем) объеме реактора (на выходе из реактора);

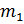- масса воды во входном (нижнем) объеме реактора;

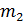- масса воды в объеме активной зоне;

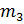- масса воды во выходном (верхнем) объеме реактора;

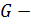массовый расход теплоносителя через реактор;

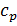- средняя по объему реактора изобарная теплоемкость воды;

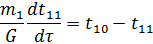
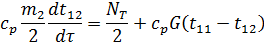
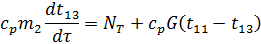
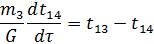
Температурный режим и тепловая мощность парогенератора

Обозначим:

t₂₁- температура на входе в парогенератор (в теплообменную трубку). Если пренебречь транспортным запаздыванием, то она принимается равной температуре на выходе из реактора

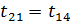
N_ПГ0 – номинальное значение тепловой мощности парогенератора;

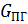- массовый расход греющего теплоносителя через ПГ;

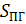– площадь теплообменной поверхности ПГ;

t₂₁₀ – номинальное значение температуры на входе в ПГ;

t₂₂₀ – номинальное значение температуры на выходе из ПГ;

t_s0 – номинальное значение температуры котловой воды (температуры кипения) в ПГ;

Θ₀ – номинальное значение среднелогарифмического температурного напора :

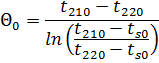
k₀ – номинальное значение коэффициента теплопередачи теплообменной поверхности ПГ

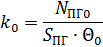
W – водяной эквивалент греющего теплоносителя ПГ:

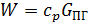
p- показатель теплообмена:

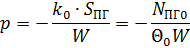
Экспоненциальный множитель теплообмена:

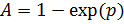
Текущее значение температуры теплоносителя на выходе из ПГ:

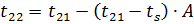
Текущее значение среднелогарифмического напора:

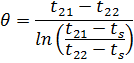
Текущая тепловая мощность парогенератора:

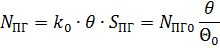
Динамика давления пара в парогенераторе

Обозначим:

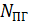– тепловая мощность парогенератора (вычислена в разделе 3);

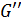- массовый расход пара из ПГ на турбину

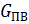– массовый расход питательной воды

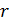- теплота парообразования

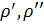- плотности воды и пара в состоянии насыщения соответственно

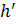- энтальпия воды в состоянии насыщения

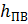- энтальпия питательной воды

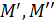- массы воды и пара в объеме ПГ соответветственно

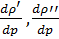– производные от плотностей воды и пара по давлению в состоянии насыщения соответственно

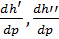- производные от энтальпий воды и пара по давлению в состоянии насыщения соответственно.

Тогда динамика давления пара в ПГ может быть описана дифференциальным уравнением:

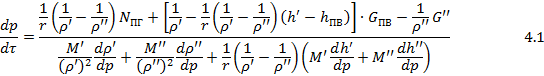
Данное уравнение может численно решаться методом Эйлера по явной численной схеме с шагом интегрирования :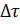

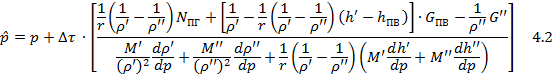
Для реализации пропорционально-интегрального закона регулирования давления пара вычисляются как текущее значение давление, так и производная (правая часть дифференциального уравнения 4.1)