Среди характеристик положения следует выделить весьма полезные УРЕЗСРЕДНЕЕ, КВАРТИЛЬ и МЕДИАНА.

Функция УРЕЗСРЕДНЕЕ (рис. 3.6) определяет среднее, отбрасывая заданный процент данных с экстремальными значениями с обеих сторон массива. (Это позволяет исключить из анализа «выбросы», см. главу 5).

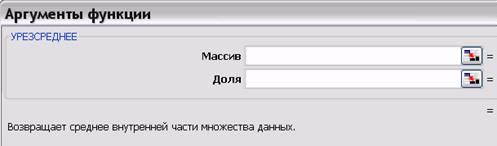
Рис. 3.6. Аргументы функции УРЕЗСРЕДНЕЕ

Кроме обычного для всех функций аргумента «Массив» в аргументах функции УРЕЗСРЕДНЕЕ присутствует аргумент «Доля» - часть точек данных, исключаемых из вычислений. Например, если «Доля» = 0,2, то из множества данных, содержащих 20 точек, исключаются 4 точки (20 x 0,2): 2 точки с наибольшими значениями и 2 точки с наименьшими значениями. УРЕЗСРЕДНЕЕ округляет количество выбрасываемых точек данных с недостатком до ближайшего целого, кратного 2. Если доля = 0,1, то 10 процентов от 30 точек данных составляют 3 точки, но для сохранения симметрии функция УРЕЗСРЕДНЕЕ исключит по одному значению из начала и конца множества.

Функция КВАРТИЛЬ (рис. 3.7) определяет квартиль множества данных. В качестве одного из аргументов функции КВАРТИЛЬ присутствует «Часть», в котором могут устанавливаться пять значений, представленных в табл. 3.1.

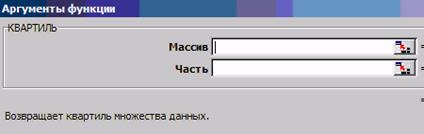
Рис. 3.7. Аргументы функции КВАРТИЛЬ

Таблица 3.1. «Оценки положения» рассеяния, определяемые различными квартилями («Часть»)

Квартиль («Часть»)	«Оценка положения»
	Минимальное значение
	Первая квартиль (25-ая персентиль)
	Значение медианы (50-ая персентиль)
	Третья квартиль (75-ая персентиль)
	Максимальное значение

Функция МЕДИАНА (вторая квартиль, см. табл. 3.1) определяет медиану заданных чисел. То есть половина чисел имеет значения большие, чем медиана, а половина чисел имеет значения меньшие, чем медиана. Если в множестве четное количество чисел, то функция МЕДИАНА вычисляет среднее двух чисел, находящихся в середине множества.

В пакете «Анализ данных» инструмент «Описательная статистика» (рис. 3.8) используется для генерации статистического отчета, содержащего информацию об основных точечных оценках рассеяния, то есть один этот инструмент может заменить множество представленных на рис. 3.5 статистических функций и тем самым сократить трудоёмкость анализа.

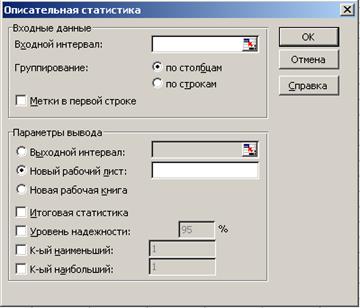
Рис. 3.8. Инструмент анализа «Описательная статистика»

С помощью инструмента «Описательная статистика» для каждого из множества массивов данных, сгруппированных по строкам или столбцам, можно вычислить и вывести на экран следующие параметры:

- среднее (статистическую оценку математического ожидания) по формуле (3.1);

- стандартную ошибку среднего 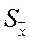(«Стандартная ошибка») по формуле (3.7);

- медиану (Ме);

- моду (Мо);

- дисперсию выборки по формуле (3.3);

- СКО по формуле (3.5);

- эксцесс по формуле (3.14);

- асимметрию (СКОС) по формуле (3.13);

- размах выборки 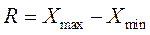(«Интервал»);

- минимальное значение выборки 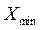(«Минимум»);

- максимальное значение выборки 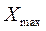(«Максимум»);

- сумму всех значений выборки («Сумма»);

- объём выборки n («Счет»);

- «Наибольший(k)» и «Наименьший(k)», см. ниже и соответствующие функции в § 2.3.1;

- «уровень надежности» (предельную ошибку выборки) для заданной доверительной вероятности: ,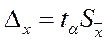

где 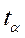- параметр распределения Стьюдента (см. § 5.2), определяемый по «уровню значимости» (называется также «коэффициент риска» и обозначается α или β) и «числу степеней свободы» (обозначается k или f) k = n - 1; 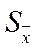- стандартная ошибка среднего.

Инструмент «Описательная статистика» (см. рис. 3.8) предлагает следующие параметры вывода:

«Итоговая статистика». Если в этом поле стоит флажок, то производится расчет всех указанных выше параметров кроме последних трёх;

«Уровень надежности». Если флажок стоит в этом поле, то производится расчет уровня надёжности (предельной ошибки выборки) 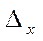(см. выше) и результат выводится в нижней части итоговой таблицы (необходимо указать значение доверительной вероятности в процентах, по умолчанию выводится 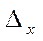для доверительной вероятности 95 %);

«К-й наименьший» и «К-й наибольший». Если это поле помечено флажком, то производится определение значений в выборке к-ого в порядке увеличения и к-ого в порядке уменьшения. (По умолчанию стоит к = 1 и определяются максимальные и минимальные значения в выборках.)

3.5 Вопросы и задания к главе 3

1. Назовите и сформулируйте сущность требований к точечным оценкам

2. Приведите формулы оценок дисперсий и стандартных отклонений.

3. Объясните понятия «квартиль» и «квантиль»

4. Как определяются погрешности оценок выборочных среднего и СКО?

5. На примере нормального распределения покажите, как изменяется форма распределения при положительных и отрицательных значениях асимметрии и эксцесса.

3.6 Дополнительная литература к главе 3.

1. ГОСТ Р 50779.21-2004. Статистические методы. Правила определения и методы расчета статистических характеристик по выборочным данным. Часть I. Нормальное распределение. - Введ. 2004-06-01. - М.: Изд-во стандартов, 2004. - 24 с.

2. ГОСТ Р 50779.22-2005 (ИСО 2602 : 1980). Статистические методы. Статистическое представление данных. Точечная оценка и доверительный интервал для среднего. - Введ. 2005-07-01. - М.: Стандартинформ, 2005. - 3 с.

3. ГОСТ Р 50779.24-2005 (ИСО 8595 : 1990). Статистические методы. Статистическое представление данных. Оценка медианы. - Введ. 2005-07-01. - М.: Стандартинформ, 2005. - 3 с.

4. ГОСТ Р 50779.25-2005 (ИСО 3494:1976). Статистические методы. Статистическое представление данных. Мощность тестов для средних и дисперсий. - Введ. 2006-01-01. - М.: Стандартинформ, 2005. - 79 с.

5. Годин А. М., Статистические средние и другие величины и их применение в различных отраслях деятельности [Текст] - 2009. - 251 с.

6. Степнов М.Н. Статистические методы обработки результатов механических испытаний: Справочник. – М.: Машиностроение, 2005. - 399 с.

7. Дюк В. Обработка данных на ПК в примерах. - СПб: Питер, 1997. - 240 с.