Точечные оценки положения, степени и характера рассеяния случайной величины на числовой оси

Целесообразно разделить точечные оценки на оценки, так или иначе характеризующие положение рассеяния на числовой оси, и оценки, характеризующие степень и характер рассеяния случайной величины.

Наиболее употребляемые показатели положения рассеяния на числовой оси достаточно условно разбиты на отдельные подгруппы (рис. 3.1).

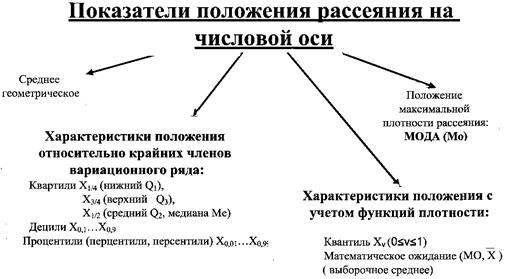
Рис. 2.1. Характеристики положения

Ниже указаны наиболее важные оценки положения.

Выборочное среднее (среднее арифметическое, математическое ожидание) случайной величины 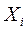обозначается как удовлетворяет всем приведённым выше требованиям к точечным оценкам. Ниже приведена формула (3.1) оценки для случая, когда значения 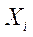разбиты по интервалам:

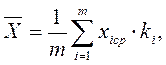(3.1)

где 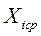- среднее значение в i-м интервале,

k_i - количество значений , попадающих в i-й интервал.

Медиана (Me) x_1/2, квартили х_1/4, х_1/2, х_3/4, децили х₀₁...х₀₉(или х_0,1...х_0,9) и процентили х₀₀₁...х₀₉₉(или х_0,01...х_0,99) делят область изменения Х соответственно на 2,4,10 или 100 интервалов.

Мода (Мо)случайной величины - наиболее вероятное значение случайной величины. Иначе - это значение случайной величины, при котором плотность распределения вероятностей имеет максимум.

Квантильсреди показателей положения рассеяния на числовой оси имеетособое значение (рис. 3.2), т.к. он непосредственно определяется интегральной функцией распределения случайной величины. Квантиль (х_γ) порядка γ распределения вероятностей (0 < γ < 1) есть такое значение х_γ случайной величины X, для которого функция распределения принимает значение γ.

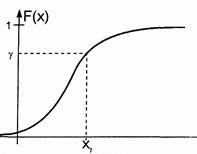
Рис. 3.2. Квантиль случайной величины X

Характеристики рассеяния относительно центра классифицируются на показатели трёх типов: «кучности» разброса, асимметрии и определяемые законом распределения (рис. 3.3).

Рис. 3.3. Характеристики степени и характера рассеяния

Ниже рассмотрены наиболее важные из характеристик рассеяния.

Выборочная дисперсия - среднее арифметическое квадратов отклонения наблюдаемых значений признака 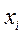от их среднего значения :

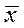(3.2)

Для генеральной совокупности оценка дисперсии по формуле (2.2) удовлетворяет всем требованиям, предъявляемым к точечным оценкам (см. выше), но применительно к выборке она является смещённой оценкой генеральной дисперсии. Для исправления выборочной дисперсии достаточно умножить ее на дробь 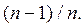Поэтому в качестве исправленной несмещённой оценки генеральной дисперсии по выборке, особенно если n относительно невелико (n < 30), обычно используют:

(3.3)

где 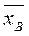- среднее значение выборки.

Если все значения случайной величины сгруппированы по k интервалам, где имеют частоты n₁, n₂,… n_j,…, n_k, то формула (3.3) принимает вид:

(3.4)

Стандартное (среднее квадратичное) отклонение (СКО)в отличие от дисперсии имеет размерность, равную размерности . Для выборки (S) и генеральной совокупности ( ) оно определяется соответственно:

(3.5)

Отсюда выборочная оценка дисперсии D_Вчасто обозначается S².

Замечания:

1. Выборочное СКО S, является лишь оценкой СКО. генеральной совокупности σ. Поэтому в отличие от σ определяется с некоторой погрешностью, характеристикой которой в свою очередь является СКО величины выборочного СКО S_S, рассчитываемая по формуле:

(3.6)

Видно, что погрешность оценки σуменьшается пропорционально увеличению квадратного корня из объёма выборки n, то есть стремится к 0 при бесконечном увеличении n.

2. С целью повышения точности (уменьшения S и S_S), например, в случае измерении какого-то параметра, это измерение повторяют несколько (n) раз, а потом усредняют. Тогда средняя квадратическая ошибка 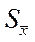среднего значения 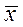уменьшается относительно СКО единичного значения x_i 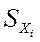, вычисляемого по формулам (3.3-3.5), пропорционально квадратному корню из количества n произведённых измерений:

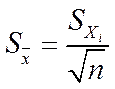, (3.7)

3. Большинство характеристик (кроме асимметрии и эксцесса, подробно описанных в § 3.3) имеют одну особенность - наличие размерности, что не даёт возможности объективно сравнивать разброс величин, имеющих разную размерность. Таким недостатком не обладает коэффициент вариации (V), представляющий собой отношение выборочного СКО S к среднему (или при n → ∞ СКО σ к МО):

V=S/ 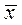(3.8)

4. Из формул (3.7) и (3.8) определяется «коэффициент вариации для среднего» :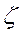

. (3.9)

5. Приведённые выше формулы универсальны, применимы для выборок, состоящих из самых различных величин. Но в ряде случаев перед проведением описанных расчётов характеристик рассеяния бывает полезна операция приведения к единичному стандартному отклонению. Для этого приводят значения x_i к среднему значению: x_{пi =} x_{i -} . Затем, умножая преобразованные значения x_пi на 1/s, получают преобразованную выборку случайной величины Z: которая имеет выборочное среднее значе­ние равное нулю и выборочное СКО равное единице.