Длинные линии и телеграфные уравнения

Цепи, которые рассматривались раннее, относятся к классу цепей с сосредоточенными параметрами, т.е. практически все магнитные поля в таких цепях сосредоточены в катушках, все электрические поля – в конденсаторах, а потери – в резисторах.

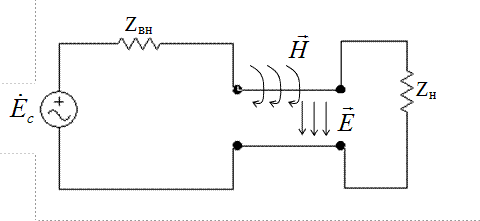
Рис.1.1. Электрическая схема цепи с распределенными параметрами

В цепях с распределенными параметрами емкость, индуктивность и потери распределены в пространстве, т.к. в дальнейшем мы будем рассматривать электрические линии, то и распространение мы будем рассматривать вдоль одной пространственной координаты. В этом случае цепи с распределенными параметрами называются длинными линиями. Простым примером такой цепи может служить двухпроводная линия передачи.

При протекании тока по проводам вокруг них существует магнитное поле 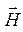, что свидетельствует о наличии индуктивности, распределенной вдоль длины линии. Между проводами линии возникает электрическое поле , что говорит о наличии емкости.

Провода и диэлектрик между проводами нагреваются. Эти обстоятельства свидетельствуют о наличии распределенных потерь.

К цепям с распределенными параметрами относят: телефонный провод, коаксионный кабель, витая пара, прямоугольный или круглый волновод, оптоволоконные линии и т.п.

Для количественной оценки распределенных параметров используют следующие погонные параметры длинной линии:

1. R₀ – погонное сопротивление потерь в проводниках линии определяется как сопротивление проводников короткозамкнутого отрезка линии длиной 1метр [Ом/м];

2. L₀ – погонная индуктивность определяется как индуктивность короткозамкнутого отрезка линии длиной 1метр [Гн/м];

3. C₀ – погонная емкостьопределяется емкость между проводами разомкнутого на конце отрезка линии длиной 1 метр [Ф/м];

4. G₀ – погонная проводимость изоляции определяется как проводимость изоляции между разомкнутыми на конце проводами отрезка линии длиной 1 метр [См/м].

Как правило, численные значения погонных параметров малы, поэтому распределенные параметры оказывают влияние на передаваемые сигналы только при большой длине линии. На промежутке эффекты, обусловленные влиянием распределенных, параметров учитывают только тогда, когда длина линии l₀ сравнима или больше длины волны сигнала:

,

где с – скорость света, f – частота.

Рассмотрим установившееся напряжение 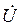и ток 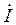в произвольном сечении длинной линии на расстоянии l от нагрузки.

Рис.1.2. Электрическая схема длинной линии

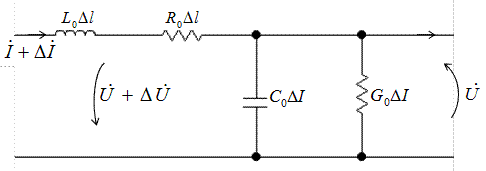
Рис.1.3. Электрическая схема четырехполюсника с сосредоточенными параметрами

Выделим на Рис.1.2 отрезок малой длины , примыкающий к рассматриваемой линии. Т.к. величина 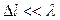, то отрезок можно представить в виде четырехполюсника с сосредоточенными параметрами (Рис.1.3). На выходных зажимах отрезка из-за влияния распределенных параметров ток и напряжение уменьшаются на величину и соответственно.

Из анализа цепи на Рис.1.3 следует, что изменение напряжения равно:

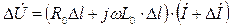
Раскрывая скобки и пренебрегая величинами 2-го порядка малости, получим выражение:

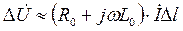
Разделив правую и левую части равенства на и переходя к пределу при 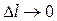, получим 1 телеграфное уравнение длинной линии:

,

,

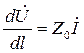где Z₀ – погонное комплексное сопротивление длинной линии.

Из этого уравнения следует, что комплексная амплитуда напряжения вдоль линии будет изменяться, если в сечении линии имеется не равный нулю ток (если производная этого уравнения не равна нулю).

Используя 1 закон Кирхгофа для выходного узла отрезка длинной линии (Рис.1.3) получим:

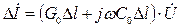
Разделив правую и левую части равенства на и переходя к пределу при 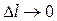, получим 2 телеграфное уравнение длинной линии:

,

,

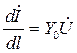где Y₀ – погонная комплексная проводимость длинной линии.

Из 2-го телеграфного уравнения следует, что при наличии напряжения в линии комплексная амплитуда тока вдоль линии будет изменяться.

ВВЕДЕНИЕ

Операционный усилитель (ОУ) получил свое название в связи с тем, что изначально он проектировался как элемент для выполнения различных математических операций над аналоговыми величинами.

Область применения ОУ широка, трудно найти современное электронное устройство, не содержащее ОУ. Это связано с тем, что на основе этого устройства решаются практически все задачи электроники. Малая стоимость, гибкость в применении и надежность определяют их широкое применение, в частности, в вычислительной технике, связи, системах управления, генерации, фильтрации и т.п.

Главной особенностью схем на ОУ является то, что выполняемые ими операции определяются подключенными к ним внешними элементами и не зависят от самого ОУ.