Численное дифференцирование функций.

Численное дифференцирование функций.

Уточнение методами Ромберга и Эйткена.

Выполнила: студент гр.МКН-206

Тимергалин Р.Д

Проверила: доцент кафедры КМ

Зиннатуллина О.Р.

Уфа 2011

СОДЕРЖАНИЕ

Введение…………………………………………………………………3

Программная реализация метода………………………………………8

Оценка погрешности результата………………………………………12

Заключение……………………………………………………………...21

Список литературы……………………………………………………..22

ВВЕДЕНИЕ

Численное дифференцирование функций

Пусть функция f(x) дифференцируема в точке x. Тогда значение производной определяется следующими пределами [1]

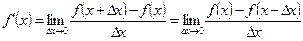
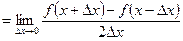. (1)

Вычисление первой производной

Для вычисления производной необходимо проведение ряда операций. Можно вычислять значения функции и проводить с ними арифметические действия. Но мы не можем вычислять пределы, поскольку это требует бесконечных затрат ресурсов (времени, памяти и т.д.). Получим приближенные формулы:

. (2)

Пусть 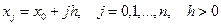- шаг разбиения. Введем обозначение 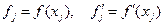и т.д. Тогда (2) можно переписать в виде

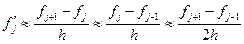. (3)

Первое из этих трех отношений носит название правой разностной производной, второе – левой, третье – центральной разностной производной.

Вычисление второй производной

Для приближенного вычисления второй производной в качестве примера используем формулу [1]

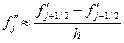, (4)

где 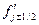определяется по формуле (3).

Отметим, что значения правой и левой разностных производных в точке 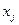одновременно являются центральными разностными производным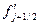и и 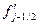, рассчитанными соответственно в точках 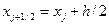и 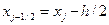(см. рис. 1).

Рис 1. Схема численного дифференцирования

Тогда

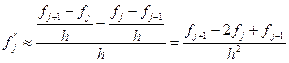. (5)

Численная фильтрация

При экстраполяции требуется априорное знание характера зависимости результата расчетов от числа узлов (или математической модели погрешности), например

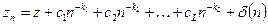, (6)

где 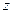– точное значение; 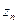– приближенный результат, полученный при числе узловых точек, равном n; 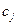– коэффициенты, которые предполагаются не зависящими от n; 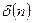– величина, полагаемая малой по сравнению с 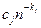при тех значениях n, которые использовались в данных конкретных расчетах, k₁,…, k_L – произвольные действительные числа (предполагается, что k₁<k₂<…< <k_L).

В математическом анализе обычно оценивается только первый член, поскольку остальные являются асимптотически (при n®¥) бесконечно малыми более высокого порядка. Однако для конечных n остальные слагаемые могут вносить существенный вклад и должны приниматься во внимание.

Если решение задачи представляет собой функцию с несколькими непрерывными производными, то можно допустить возможность его разложения по формуле Тейлора, тогда 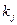– это часть ряда натуральных чисел. Тогда к задаче нахождения предельного при 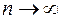значения z можно подойти как к задаче интерполяции зависимости 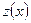от параметра 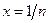алгебраическим многочленом с последующей экстраполяцией до 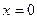. Есть и другой подход, приводящий при условии постоянства 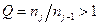к тому же алгоритму, но не требующий целочисленности 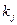. Это решение задачи численной фильтрации, т.е. последовательное устранение степенных слагаемых суммы (6) при сохранении значения константы z. 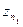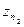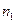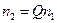Рассмотрим два значения , , вычисленные при числе узлов, равном и соответственно. Составим линейную комбинацию

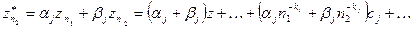
и потребуем, чтобы, суммарный коэффициент при z был равен 1, а при 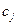(для определенного j) равен 0. Отсюда получим формулу фильтрации, которая совпадает с экстраполяционной формулой Ричардсона [1]

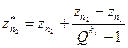. (7)

Проводя последовательно экстраполяцию по всем парам соседних значений, получим отфильтрованную зависимость, не содержащую члена с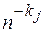

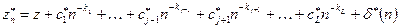, (8)

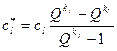где . (9)

Заметим, что отфильтрованная последовательность 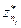содержит на один член меньше, чем исходная. Если она содержит больше одного члена, то ее также можно отфильтровать, устранив степенную составляющую с 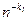. Операции фильтрации можно повторять последовательно для 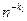,…, , 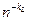если исходная последовательность содержит достаточное количество членов. Результаты экстраполяций удобно представлять в виде треугольной матрицы

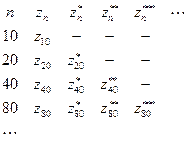(10)

Применение повторной экстраполяции при k_j=j известно под названием метода Ромберга. При его применении возникает ряд ограничений.

Применение повторной экстраполяции приводит к изменению коэффициентов суммы (6). При 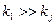увеличение абсолютной величины коэффициентов может оказаться весьма существенным. Это ограничивает число возможных экстраполяций.

Величина 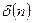в (6) может оказаться суммой регулярной составляющей, имеющей вид 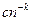, и нерегулярной составляющей 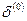, обусловленной погрешностью исходных данных, которая, например, связана с ограниченной разрядностью чисел в машинном представлении. Тогда исходная нерегулярная часть погрешности, содержащаяся в вычисленных значениях 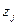, при каждой экстраполяции умножается на коэффициент

.

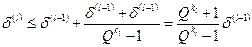Для метода Ромберга, применяемого к последовательности (6) при 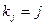, произведение таких множителей ограничено числом, приблизительно равным 8 (получено численно), т.е. метод Ромберга является устойчивым к погрешности исходных данных, но сам уровень нерегулярной погрешности может ограничить число возможных экстраполяций.

Процесс Эйткена

При оценке погрешности частичных сумм значение k в (2.4) может быть неизвестно. В этом случае можно использовать следующую модификацию правила Ричардсона. Вычислим три значения z₁, z₂, z₃ при трех номерах последовательности: n, nQ, nQ² и составим систему трех уравнений [1, 9]

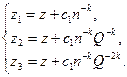(11)

Найдем разности

,

,

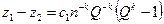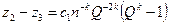и, разделив одну на другую, определим Q^k

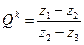. (12)

Теперь можно найти z

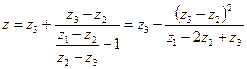. (13)

Как и в рассмотренных ранее случаях, мы нашли экстраполированное (уточненное) значение z=z*, а вместе с ним и оценку погрешности z_i-z*.

Этот способ экстраполяции при неизвестном порядке точности принято называть алгоритмом Эйткена или d²-алгоритмом, который в более общем случае применяется для экстраполяции векторных последовательностей

.

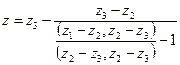В последнем выражении z_i – векторы, а скобками обозначается скалярное произведение.

Критерий размытости оценки

Оценка погрешности по правилу Рунге сводится к сравнению значения z_n с экстраполированным значением 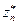. Поскольку эта оценка справедлива при допущении, что величина 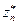точнее, чем z_n, то необходима проверка справедливости этого допущения. Это можно сделать следующим образом. Повторим процесс экстраполяции и получим значение 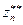. Разность 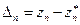представляет собой оценку погрешности приближенного значения z_n.. Разность 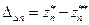является оценкой погрешности экстраполированного значения 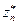или оценкой погрешности оценки погрешности (рис. 10). Отношение 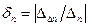имеет смысл относительной размытости оценки погрешности.

Если 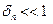, то это означает, что относительная размытость оценки 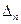мала, и такой оценке можно доверять.

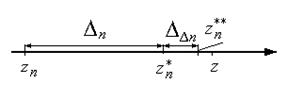
Рис. 10. Размытость оценки погрешности

Пусть оценка погрешности представляется в виде интервала 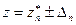. Для определения порогового значения d_n для принятия или отклонения полученной оценки желательно на основании имеющейся информации установить, не может ли при гипотетическом продолжении экстраполяций произойти переход получающихся значений левее 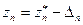или правее 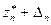. Для этого предположим, что при последующих гипотетических экстраполяциях значение 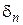, как коэффициента уменьшения расстояния между соседними экстраполированными значениями, будет сохраняться: 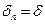. Тогда предельное удаление предельного значения от 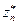определяется суммой геометрической прогрессии 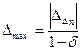. Отсюда следует неравенство

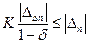, (14)

где K³1 – коэффициент «запаса» надежности оценки. Необходимость введения коэффициента K вызвано желанием получать достаточно надежные оценки в условиях неопределенности, вызванной влиянием нерегулярных составляющих погрешности. Тогда получим условие (критерий принятия оценки)

.

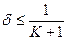Примем величину K=2. Тогда пороговое значение 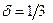, тогда при 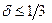оценка принимается, а при 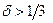отвергается. Это же значение было получено эмпирически при анализе реальных численных данных [9].

Заключение

В результате выполненной работы “численное дифференцирование методом левой, правой и центрально-разностной формулами“ были получены следующие результаты. Были вычислены погрешности по методу Ромберга и Эйткена, и получены следующие графики.

СПИСОК ЛИТЕРАТУРЫ

1. Бахвалов Н.С., Жидков Н.П., Кобельков Г.М. Численные методы. -М.: Наука, 2004. -636 с.

2. Самарский А.А. Численные методы математической физики.-М.: Научный мир, 2000.-316с.:

3. Самарский А.А. Задачи и упражнения по численным методам.-М.: Эдиториал УРСС, 2000.-208с

4. Самарский А. А. Математическое моделирование. Идеи. Методы. Примеры / А. А. Самарский , А. П. Михайлов.-2-е изд., испр..-М.: ФИЗМАТЛИТ, 2005.-320 с.;

5. Крылов В.И., Бобков В.В., Монастырный П.И. Вычислитель­ные методы. Т. I, II. -М.: Наука, 1987. -600 с.

6. Васильков Ю.В. Компьютерные технологии вычислений в математическом моделировании: Учеб.пособие.-М.: Финансы и статистика, 2001.-256с.

7. Подвальный С. Л. Численные методы и вычислительный эксперимент: учебное пособие для вузов / С. Л. Подвальный, Л. В. Холопкина , Д. В. Попов; УГАТУ; Воронеж. гос. техн. ун-т.-Уфа: УГАТУ, 2005.-224 с.; 21 см.-Библиогр.: с. 220-224 (49 назв.).-ISBN 5-86911-491-8.

8. Житников В.П., Шерыхалина Н.М., Ураков А.Р. Линейные некорректные задачи. Верификация численных результатов. Учебное пособие. -Уфа: УГАТУ, 2002. -91 с.

9. Smith D.A., Ford W.F. Acceleration of linear and logarithmic convergence. – SIAM J. Numer. Anal., 1979, v. 16. -P. 223-240.

10. Smith D. A., Ford W. F. Numerical comparisons of non-linear convergence accelerations. – Mathematics of Computation, 1982, v. 38, 158. -P. 481–499.

11. Прудников А. П. Интегралы и ряды. В 3-х т. / А. П. Прудников, Ю. А. Брычков, О. И. Маричев.-М.: ФИЗМАТЛИТ, 2003.

Численное дифференцирование функций.