Принцип суперпозиции (наложения)

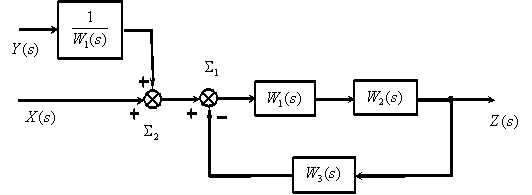
Применим рассмотренные правила для упрощения структурной схемы

Рис. 1

Процесс преобразования, который часто называют свертыванием структурной схемы, выглядит следующим образом.

1. Перенесем суммирующее звено через динамическое звено .

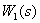2. Поменяем местами суммирующие звенья и .

3. Преобразуем последовательно включенные динамические звенья 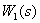и .

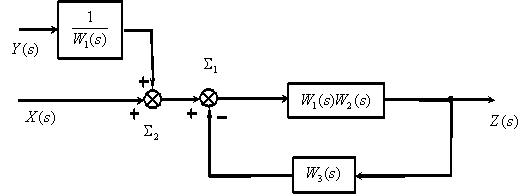
4. Преобразуем замкнутый контур с отрицательной обратной связью ( ).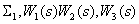

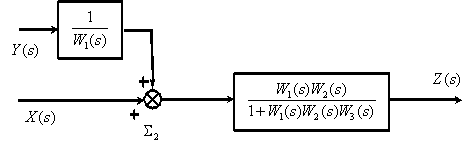
5. Перенесем суммирующее звено вправо.

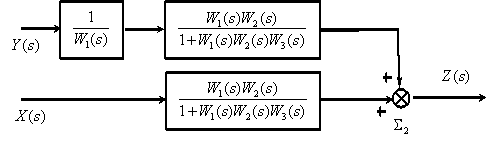
6. Преобразуем последовательно включенные звенья..

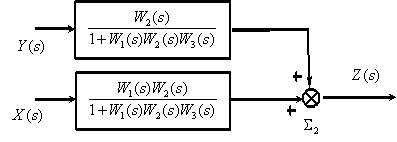
В соответствии с полученной структурной схемой запишем операторное уравнение –

(1)

Уравнение показывает, что является линейной комбинацией изображений входных сигналов, взятых с коэффициентам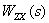и и 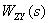. Выясним смысл этих коэффициентов на примере коэффициента 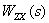. Для этого положим в (1) 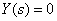, тогда получим –

(2)

Таким образом, из (2) следует, 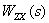– это передаточная функция динамического звена, к которому свернута структурная схема в предположении, что изображения всех входных сигналов, кроме , равны нулю.

Теперь становится ясным смысл и самого операторного уравнения (1), описывающего систему. Он заключается в том, что реакция линейной системы на совместно действующие входные сигналы может быть определена в виде суммы частичных реакций, каждая из которых вычисляется в предположении, что на систему действует только один входной сигнал, а остальные равны нулю.

По сути – это формулировка фундаментального принципа, который называют принципом наложения или суперпозиции. Этот принцип можно рассматривать как дополнение к правилам эквивалентных преобразований структурных схем и активно использовать на практике.

Практически принцип суперпозиции для нахождения конкретной передаточной функции используют следующим образом. Полагают равными нулю все входные сигналы, кроме необходимого сигнала, а затем выполняют преобразование структурной схемы в одно динамическое звено.

23. Понятие передаточной функции системы и комплексного коэффициента передачи. Методы получения этих характеристик.

Комплексный коэффициент передачи линейного звена – это отношение комплексной амплитуды сигнала, снимаемого с выхода звена, к комплексной амплитуде сигнала, поданного на его вход:

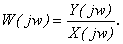(2.5)

Здесь Y(jw) – комплексная амплитуда выходного сигнала, а X(jw) – комплексная амплитуда входного сигнала, w имеет физический смысл частоты.

Преобразование дифференциальных уравнений по Лапласу дает возможность ввести удобное понятие передаточной функции, характеризующей динамические свойства системы.Передаточной функцией называется отношение изображения выходного воздействия Y(р) кизображению входного X(р) при нулевых начальных условиях.

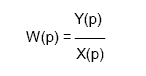
Передаточная функция является дробно-рациональной функцией комплексной переменной:

где:

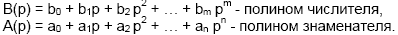
Передаточная функция имеет порядок, который определяется порядком полинома знаменателя (n).
Из формулы (2.6) следует, что изображение выходного сигнала можно найти как

Так как передаточная функция системы полностью определяет ее динамические свойства, то первоначальная задача расчета САР сводится к определению ее передаточной функции. При расчете настроек регуляторов широко используются достаточно простые динамические модели промышленных объектов управления.

В частности, использование моделей инерционных звеньев первого или второго порядка с запаздыванием для расчета настроек регуляторов обеспечивает в большинстве случаев качественную работу реальной системы управления. В зависимости от вида переходной характеристики (кривой разгона) задаются чаще всего одним изтрех видов передаточной функции объекта управления:

1. В виде передаточной функции инерционного звена первого порядка:

где: К - коэффициент усиления,
Т - постоянная времени,
- запаздывание, которые должны быть определены в окрестности номинального режима работы объекта.

2. Для объекта управления без самовыравнивания передаточная функция имеет вид:

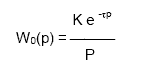
3. Более точнее динамику объекта описывает модель второго порядка с запаздыванием:

24. Понятие КПД. Правило Муавра.

Корнем 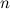-ой степени из комплексного числа называется такое комплексное число 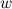, 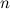-я степень которого равна , то есть

Корень 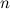-ой степени из комплексного числа обозначается символом 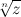и на множестве комплексных чисел имеет ровно 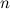значений.

Если комплексное число задано в тригонометрической форме: 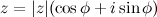, то все значения корня 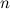-ой степени вычисляются по формуле Муавра (Абрахам де Муавр (1667 - 1754) - английский математик):

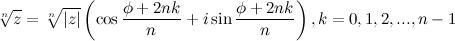
Геометрически все значения корня лежат на окружности радиуса с центром в начале координат и образуют правильный -угольник.

Коэффициент полезного действия это характеристика эффективности работы, какого либо устройства или машины. КПД определяется как отношение полезной энергии на выходе системы к общему числу энергии подведенной к системе. КПД величина безразмерная и зачастую определяется в процентах.

Коэффициент полезного действия

Формула 1 — коэффициент полезного действия

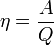
где—A полезная работа

—Q суммарная работа, которая была затрачена

25. Единичное воздействие и воздействие в виде дельта-функции. Их назначение для определения характеристик систем.

Описание сигналов. Для описания сигналов используются функции вре­мени. Выделяют два специальных сигнала: импульсное воздействие в виде дельта - функции и единичную ступенчатую функцию. Им соответствуют две системные характеристики- импульсная переходная и единич­ная переходная функции.

Дельта-функция (асимметричная) определяется формулой

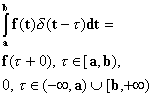
справедливой для любой кусочно-непрерывной функции времени . Аналогично определяются производные дельта - функции:

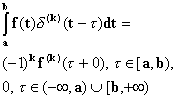
где - любая функция, имеющая кусочно-непрерывную производную соот­ветствующего порядка.