Алгоритм построения триангуляции Делоне
Впервые задача построения сети неперекрывающихся треугольников была поставлена в 1934 году в работе советского математика Б. Н. Делоне, который сформулировал и соответствующие условия.
В математике задачей построения триангуляции по заданным точкам называют задачу их попарного соединения непересекающимися отрезками так, чтобы образовалась сеть треугольников.
| Рис. Элементы триангуляции Делоне |
| a a |
| b b |
| Грань |
| Узел |
| Ребро |
узлы (вершины треугольников), ребра (стороны) и грани (собственно треугольники).
Построенная триангуляция может быть:
• выпуклой (если таковым будет минимальный многоугольник, охватывающий область моделирования),
• невыпуклой (если триангуляция не является выпуклой) и оптимальной (если сумма длин всех ребер минимальна).
Сеть таких треугольников называется триангуляцией Делоне, если она удовлетворяет некоторым условиям:
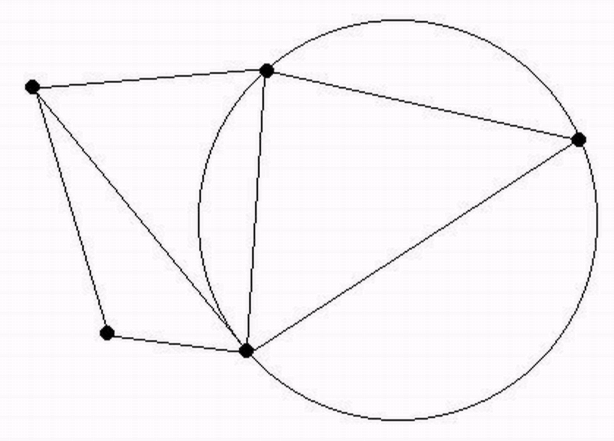
• внутрь окружности, описанной вокруг любого треугольника, не попадает ни одна из исходных точек;
• триангуляция является выпуклой и удовлетворяет сформулированному выше условию Делоне;
• сумма минимальных углов всех треугольников максимальна из всех возможных триангуляций;
• сумма радиусов окружностей, описанных около треугольников, минимальна среди всех возможных триангуляций.
Первый из названных выше критериев (внутрь окружности, описанной вокруг любого треугольника, не попадает ни одна из исходных точек) построения триангуляции Делоне, называемый круговым, является одним из основных и проверяется для любой пары треугольников с общими гранями. Математическая интерпретация критерия вытекает из рисунка.
| Рис. Элементы триангуляции Делоне |
| a a |
| b b |
| Грань |
| Узел |
| Ребро |
Многие алгоритмы построения триангуляции Делоне используют следующую теорему:
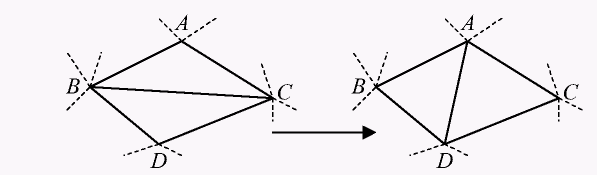
Теорема 1. Триангуляцию Делоне можно получить из любой другой триангуляции по той же системе точек, последовательно перестраивая пары соседних треугольников ABC и BCD, не удовлетворяющих условию Делоне, в пары треугольников ABD и ACD.
Такую операцию перестроения часто называют флипом.
На основе определения триангуляции Делоне и соответствующих условий на практике обычно используют несколько способов проверки:
– проверка через уравнение описанной окружности;
– проверка с заранее вычисленной описанной окружностью;
– проверка суммы противолежащих углов;
– модифицированная проверка суммы противолежащих углов.

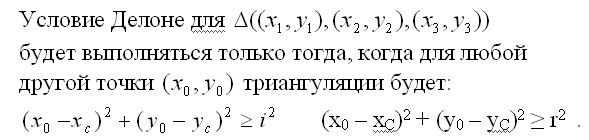
Полиномиальные методы
Полиномиальные способы предполагают представление моделируемой поверхности полиномом второй - пятой степени вида
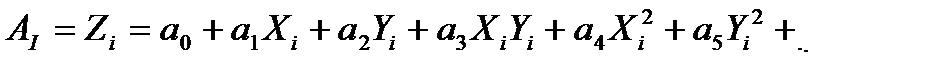
Для отыскания неизвестных коэффициентов полинома для каждой опорной точки составляют одно уравнение поправок вида
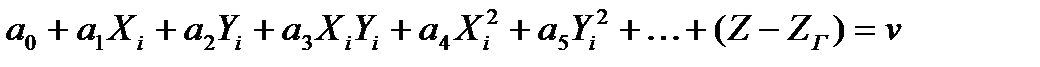
где свободный член (Z – ZГ) представляет собой уклонение вычисленной по формуле (5.7) отметки (Z) с приближенными значениям коэффициентов полинома от исходной (ZГ). Полученную систему решают последовательными приближениями, в каждом из которых неизвестные находят методом наименьших квадратов, под условием [pv 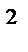 ]= min. Найденные таким образом коэффициенты а0...аi уравнений (5.7) используют для интерполяции высот точек, расположенных в области моделирования.
]= min. Найденные таким образом коэффициенты а0...аi уравнений (5.7) используют для интерполяции высот точек, расположенных в области моделирования.
Кусочно-полиномиальные способы предполагают деление области моделирования на участки, подбор для каждого участка своего локального полинома вида (5.7) и последующую связь локальных полиномов с помощью переходных уравнений. Во всех случаях возникают переопределенные системы, которые решаются под условием минимума суммы квадратов расхождений высот точек реальной и аппроксимирующей поверхностей.
Сходные по характеру решения используют способы, основанные на применении рядов Фурье (разложений по сферическим гармоникам), различного рода сплайнов (кубических, бикубических, на многообразиях и др.) и т. п. [3].
На русский язык термин "spline" переводится как "гибкая рейка" или "плавная кривая" [5].
Сплайны используются для сглаживания линий при отображении гладких поверхностей (поле и т.д.).
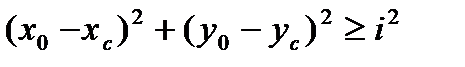
(x0 – xC)2 + (y0 – yC)2 ≥ r2 . (1)
