Особенности отработки средних и больших перемещений в позиционной системе

В большинстве приводов наилучшим считается такой переходный процесс отработки средних перемещений, когда скорость двигателя в процессе отработки заданного угла изменяется по треугольному графику, т.е. при старт-стопном управлении это позволяет в полной мере использовать перегрузочную способность двигателя и исключает возникновение перерегулирования в переходном процессе. Для того чтобы в замкнутой системе привода при обработке заданного углового перемещения происходило управление двигателем, близкое к старт-стопному, необходимо обеспечить вполне определенное, соответствующее этому перемещению, значение передаточного коэффициента РП.

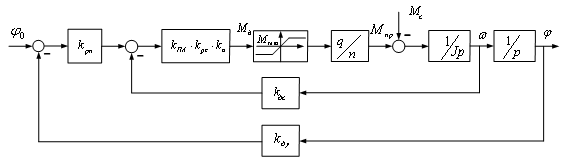
Рис. 2. Структурная схема следящего привода в режиме средних и больших отклонений угла.

kдуkрпδφ1=ω1kдс

ω1=ε1t1=1/2×ε1(1+μ)t0, (1)

где ε=(M–Mс)/J, μ=Mс/M – относительный момент на валу объекта регулирования, M – момент двигателя, приведенный к валу объекта регулирования, при насыщении регулятора скорости и регулятора тока, t0 время переходного процесса при старт-стопном управлении. Отметим, что в данном случае время t0, не регламентировано, а зависит от параметров привода и заданного значения угла. Эту зависимость просто найти из (1.55). Разрешим его относительно t0.При этом получим

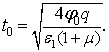
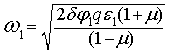(4)

Из последнего выражения следует, что значение коэффициента регулятора при переходном процессе при больших и средних отклонениях должно меняться по параболическому закону. В этом случае при любых начальных значениях отклонение угла φ0 будет обеспечен оптимальный переходный процесс отработки рассогласования без перерегулирования и момента нагрузки Mс.

Нелинейная характеристика регулятора, соответствующая выражению (4) 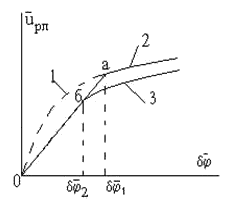представлена на рис. 2 (кривая 1).

Рис. 2. Выходная характеристика нелинейного регулятора

(25)))))))))))))))))))))))))))))))))))))))

27.Применение параболического регулятора положения и регулятора с переменной структурой В условиях возрастания требований к точности соблюдения режимными переменными объектов управления (ОУ) установленных регламентов и роста потерь при их нарушениях, задача совершенствования алгоритмов регулирования сохраняет свою актуальность и остается в числе традиционных задач теории автоматического управления. Вместе с тем, как показывает практика, когда в качестве объектов управления выступают технологические агрегаты (процессы) (ТА ТП), то разработчики систем автоматического регулирования (САР), в подавляющем большинстве случаев используют простейшие ПИ-, ПИД-алгоритмы регулирования. Это обстоятельство может быть объяснено следующими двумя взаимообусловленными факторами.Во-первых, ТА как ОУ имеют специфические особенности по сравнению с такими объектами, как манипуляторы, электропривод, усилители, транспортные (мобильные) средства. Основные из них: а) физическая распределенность каналов управления ТА, проявляющаяся в значительных запаздываниях реакции управляемых переменных на управляющие воздействия; б) большое количество факторов весьма существенно влияющих на работу ТА, но практически недоступных для измерения (характеристики сырьевых и энергетических потоков, состояние рабочих органов и активных зон ТА), проявляющихся как неконтролируемые возмущения (координатные, параметрические), и изменяющие значения управляемых переменных, свойства каналов управления,Во-вторых, для ПИД-регуляторов, используемых в САР, для объектов технологического типа имеется инфраструктура инженерной поддержки их применения. Она включает в себя типовые модели динамики каналов регулирования, упрощенные процедуры параметрической идентификации этих типовых моделей, типовые методики расчета настроечных параметров регуляторов или их начальных приближений, типовые аппаратные и программные средства, реализующие эти алгоритмы [1 Если выходной сигнал регулятора в каждой точке является функцией ошибки, то и в точке, соответствующей моменту времени t2 выходной сигнал будет также являться функцией этой ошибки. Для этого выходной сигнал должен быть равен

Uрп* = . 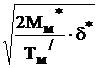Такую статическую характеристику имеет параболический регулятор (рисунок 6.17).

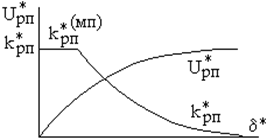
Найдем коэффициент параболического регулятора

Крп*= 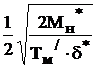Осциллограмма сигналов при отработке заданных перемещений позиционной системой с параболическим регулятором представлена на рисунке 6.18.

Uрп*(нач)
= Крп*×qз* = 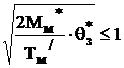q*З(МАКС) = .

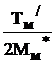Сравнивая с настроечным перемещение q*З(МАКС) можно сделать вывод, что оптимальность отработки сигналов с параболическим регулятором положения возможно в диапазоне перемещений, вдвое меньше настроечных q*З(МАКС) = q*З(настр)/2.

В момент времени t2 Uрп* = .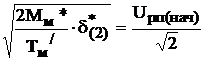

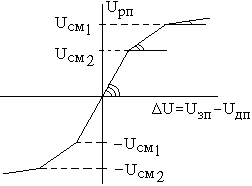Рисунок 6.20 Рисунок 6.21

Для общего случая практическая реализация параболического регулятора положения (ПРП) имеет вид, представленный на рисунке 6.19. При практической реализации начальный угол должен быть ограничен коэффициентом, который имеет контур положения в режиме малых перемещений. Реализация такой нелинейной зависимости осуществляется методом кусочно-линейной аппроксимации (рисунок 6.20).