Схема исследования на экстремум функции двух переменных.

1. Найти частные производные функции 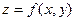: 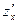и .

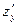2. Решить систему уравнений , 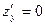и найти критические точки функции.

3. Найти частные производные второго порядка, вычислить их значения в критических точках и с помощью достаточного условия сделать вывод о наличии экстремумов.

4. Найти экстремумы функции.

Пример 23.Найти экстремумы функции .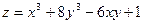

Решение.

1) Найдем частные производные .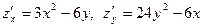

2) Решим систему уравнений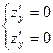

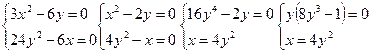
3) Найдем частные производные второго порядка и их значения в критических точках: 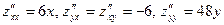. В точке 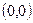получим: значит, в точке 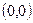экстремума нет. В точке 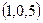получим: значит, в точке 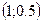минимум.

4) .

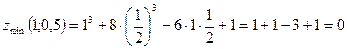Ответ.

Глобальный экстремум (наибольшее и наименьшее значение функции).

Наибольшее и наименьшее значения функции нескольких переменных, непрерывной на некотором замкнутом множестве, достигаются или в точках экстремума, или на границе множества.

Схема нахождения наибольшего и наименьшего значений.

1) Найти критические точки, лежащие внутри области, вычислить значение функции в этих точках.

2) Исследовать функцию на границе области; если граница состоит из нескольких различных линий, то исследование необходимо провести для каждого участка отдельно.

3) Сравнить полученные значения функции и выбрать наибольшее и наименьшее.

Пример 24.Найти наибольшее и наименьшее значения функции в прямоугольнике .

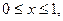
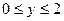Решение. 1) Найдем критические точки функции, для этого найдем частные производные: 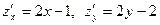, и решим систему уравнений:

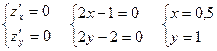
Получили критическую точку A 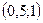. Полученная точка лежит внутри заданной области.

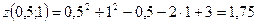
y 2

B C

. A

0 D x

Границу области составляют четыре отрезка: и . найдем наибольшее и наименьшее значение функции на каждом отрезке.

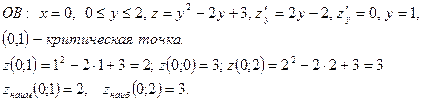
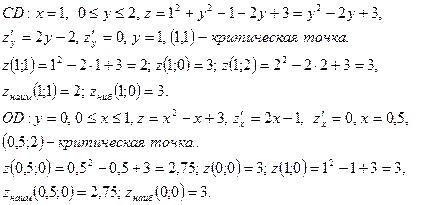
4) Сравним полученные результаты и получим, что 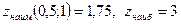в точках .

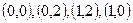Глава 4. Интегрально исчисление.

Неопределенный интеграл

Определение 1. Функция 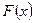называется первообразной для 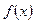, если .

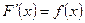Определение 2. Неопределенным интегралом от функции f(x) называется совокупность всех первообразных для этой функции.

Обозначение: 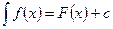, где c - произвольная постоянная.

Свойства неопределенного интеграла

1. Производная неопределенного интеграла: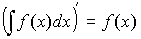

2. Дифференциал неопределенного интеграла: .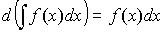

3. Неопределенный интеграл от дифференциала: .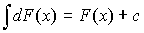

4. Неопределенный интеграл от суммы (разности) двух функций:

;

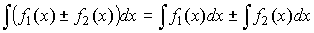5. Вынесение постоянного множителя за знак неопределенного интеграла:

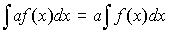
Таблица неопределенных интегралов

1)

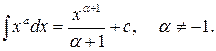
2)

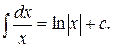
3)

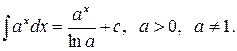
Если 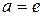, то .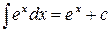

4)

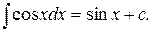
5)

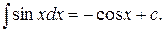
6)

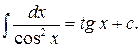
7)

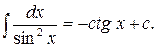
8)

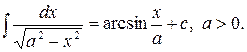
9)

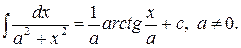
10)

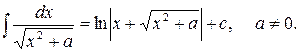
11)

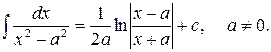
Все формулы справедливы также в случае, если переменную 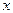заменить на некоторую другую функцию. Так, если в формуле 2 заменить 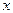на 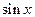, то получим, что

.

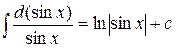Основные методы интегрирования

1. Использование свойств неопределенного интеграла.

Пример 25.

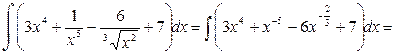
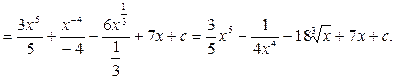
2. Подведение под знак дифференциала.

Пример 26.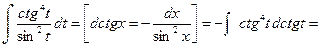

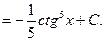
3. Метод замены переменной:

а) замена 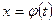в интеграле :

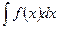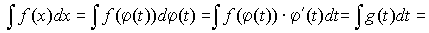
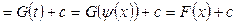, где

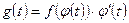- функция, интегрируемая легче, чем исходная;

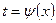- функция, обратная функции ;

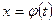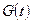- первообразная функции .

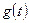Пример 27.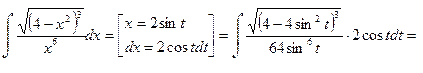

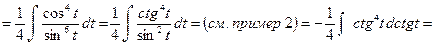
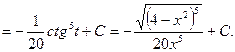
б) замена 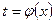в интеграле вида:

;

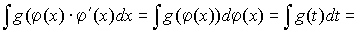
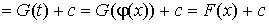Пример 28.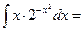

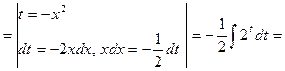
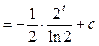
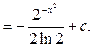
Пример 29.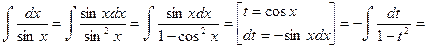

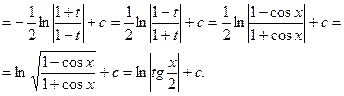
4. Метод интегрирования по частям:

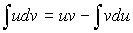
Пример 30.

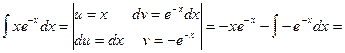
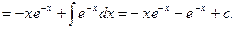
Пример 31.

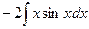
Возьмем отдельно интеграл

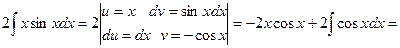
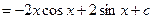
Вернемся к нашему интегралу:

Определенный интеграл

Определение. Пусть на некотором интервале 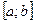задана непрерывная функция 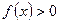. Построим ее график.

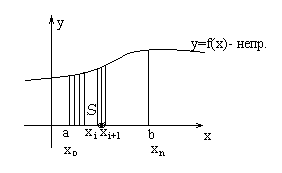
Фигура, ограниченная сверху кривой , слева и справа прямыми 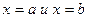и снизу отрезком оси абсцисс между точками a и b, называется криволинейной трапецией.

S – область – криволинейная трапеция.

Разделим интервал точками и получим:

Интегральная сумма:

Определение. Определенным интегралом называется предел интегральной суммы.

Свойства определенного интеграла:

1. Постоянный множитель можно выносить за знак интеграла.

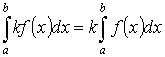
2. Интеграл от алгебраической суммы двух функций равен сумме интегралов этих функций

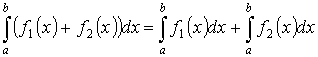
3. Если отрезок интегрирования разбит на части, то интеграл на всем отрезке равен сумме интегралов для каждой из возникших частей, т.е. при любых a, b, c

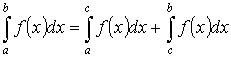
4. Если на отрезке 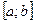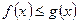, то и

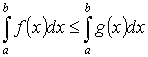
5. Пределы интегрирования можно менять местами, при этом меняется знак интеграла

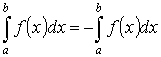
6. Интеграл в точке равен 0:

1. 

8. (“о среднем”) Пусть y = f(x) интегрируема на [a ,b] Тогда 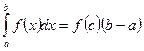, где 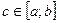, f(c) – среднее значение f(x) на [a ,b]: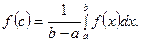

9. Формула Ньютона-Лейбница

, где F(x) – первообразная для f(x).

Методы вычисления определенного интеграла.

1. Непосредственное интегрирование

Пример 32.

а)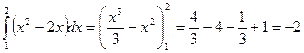

б)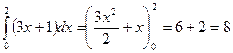

в)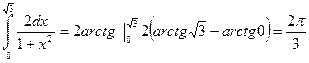

г)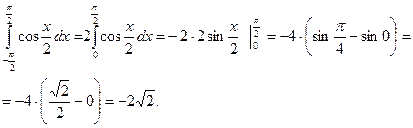

5.

2. Замена переменных под знаком определенного интеграла.

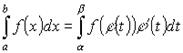
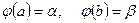
Пример 33.

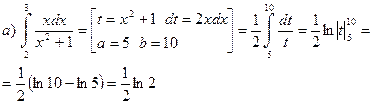
б)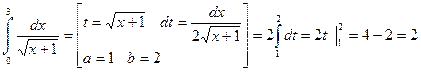

3. Интегрирование по частям в определенном интеграле.

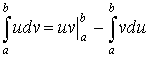
Пример 34:

а)

б)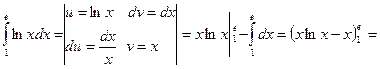

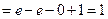
в)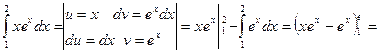

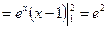
г)

д)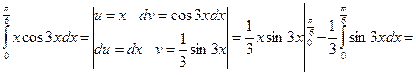

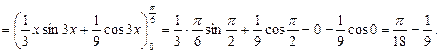
4.3. Несобственные интегралы.

Понятие несобственного интеграла связано с понятием определенного интеграла. Нельзя вычислить определенный интеграл при неограниченных пределах и в точках, в которых подынтегральная функция не существует. Обобщением определенного интеграла в этих случаях и служит несобственный интеграл.

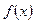Определение. Несобственным интегралом (с бесконечным пределом интегрирования) от функции на промежутке 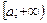называется предел функции при , т.е.

.

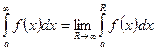Аналогично, .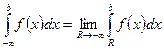

Интеграл с двумя бесконечными пределами

.

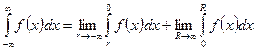Определение. Несобственным интегралом (от неограниченной функции 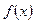) 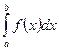на промежутке называется предел

.

Несобственным интегралом (от неограниченной функции 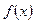) 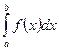на промежутке 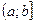называется предел

.

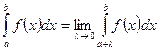Если предел существует и конечен, то несобственный интеграл называется сходящимся (к данному пределу), в противном случае – расходящимся. В случае интеграла с двумя бесконечными пределами, оба предела должны быть конечными, если хотя бы один предел не существует или бесконечен, то интеграл будет расходящимся.

Пример 35. Найти несобственные интегралы, если они сходятся.

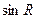а) , но предел функции не существует при , значит данный интеграл расходится.

б) .

в)

.

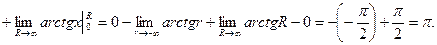
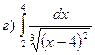Т.к. при 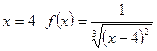не имеет смысла, то данный интеграл является несобственным и, значит:

.

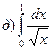Т.к. при не имеет смысла, то данный интеграл является несобственным и, значит:

Рекомендуемая литература.

Основная.

1. М.С. Красс, Б.П. Чупрынов. Основы математики и ее приложение в экономическом образовании: Учебник. – 4-е изд., исп. – М.: Дело, 2003.

2. М.С. Красс, Б.П. Чупрынов. Математика для экономических специальностей: Учебник. – 4-е изд., исп. – М.: Дело, 2003.

3. М.С. Красс, Б.П. Чупрынов. Математика для экономического бакалавриата. Учебник. – 4-е изд., исп. – М.: Дело, 2005.

4. Высшая математика для экономистов. Учебник для вузов / Н.Ш. Кремер, Б.А. Путко, И.М. Тришин, М.Н. Фридман; Под ред. проф. Н.Ш. Кремера, - 2-е изд., перераб. и доп. – М: ЮНИТИ, 2003.

5. Кремер Н.Ш, Путко Б.А., Тришин И.М., Фридман М.Н.. Высшая математика для экономических специальностей. Учебник и Практикум (части I и II) / Под ред. проф. Н.Ш. Кремера, - 2-е изд., перераб. и доп. – М: Высшее образование, 2007. – 893с. – (Основы наук)

6. Данко П.Е., Попов А.Г., Кожевникова Т.Я. Высшая математика в упражнениях и задачах. М. высшая школа. 1999.

Дополнительная

1. И.И. Баврин, В.Л. Матросов. Высшая математика. «Гуманитарный издательский центр Владос», 2002.

2. И.А. Зайцев. Высшая математика. «Высшая школа», 1998.

3. А.С. Солодовников, В.А. Бабайцев, А.В. Браилов, И.Г. Шандра. Математика в экономике / в двух частях/. М. Финансы и статистика. 1999.

Оглавление.

Введение. 3

1. Общие методические рекомендации 3

2. Программа курса. 3

3. Задания к контрольной работе. 8

4. Методические указания по выполнению контрольной работы. 25

Тема 1. Введение в анализ. 25

Тема 2. Дифференциальное исчисление. 33

Тема 3. Функции нескольких переменных. 40

Тема 4. Интегральное исчисление. 48

4.1. Неопределенный интеграл. 48

4.2. Определенный интеграл. 53

4.3. Несобственные интегралы. 58

Рекомендуемая литература. 61