Фундаментальная система решений однородной системы уравнений

Фундаментальная система решений – это множество линейно независимых векторов 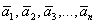, каждый из которых является решением однородной системы, кроме того, решением также является линейная комбинация данных векторов 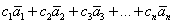, где – произвольные действительные числа.

Количество векторов фундаментальной системы рассчитывается по формуле:

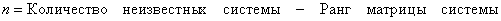
Однако в практических заданиях гораздо удобнее ориентироваться на следующий признак: количество векторов фундаментальной системы равно количеству свободных неизвестных.

Представим общее решение Примера №3 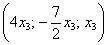в векторной форме. Свободная переменная в данном случае одна, поэтому фундаментальная система решений состоит из единственного вектора . Как его найти? Для этого свободной переменной нужно придать произвольное ненулевое значение. Проще всего, конечно же, выбрать 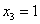и получить: .

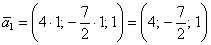Координаты вектора 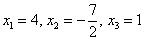должны удовлетворять каждому уравнению системы, и будет не лишним в этом убедиться.

Ответ следует записать в виде линейной комбинации векторов фундаментальной системы. В нашей ситуации линейная комбинация состоит из одинокого слагаемого. Общее решение однородной системы я буду обозначать через вектор (подстрочный индекс расшифровывается «Общее Однородной»).

Ответ: общее решение: , где (любое вещественное число)

Придавая параметру 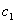различные действительные значения, можно получить бесконечно много частных решений, например, если 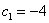, то вектор частного решения однородного уравнения («Частное Однородной») равен:
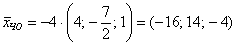, то есть набор переменных 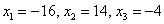удовлетворяет каждому уравнению системы.

Это мы рассмотрели традиционный способ построения фундаментальной системы в так называемом нормальном виде – когда свободным переменным придаются исключительно единичные значения. Но правила хорошего математического тона предписывают избавляться от дробей, если это возможно. Поэтому в данном случае можно взять и из общего решения системы 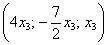получить вектор с целыми координатами: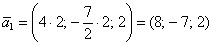

И тогда ответ запишется в эквивалентной форме:
, где (любое вещественное число)

Оба варианта ответа правильны, однако чайникам я всё-таки рекомендую классику жанра.

Поблагодарим задачник Рябушко за предоставленные примеры и перейдём к более основательным системам:

Пример 4

Решить однородную систему линейных уравнений

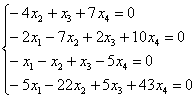
Ответ записать с помощью фундаментальной системы решений

Самостоятельно, plz. Примерный образец оформления в конце урока.

Закинем в копилку знаний ещё один полезный факт:

Взаимосвязь решений неоднородной
и соответствующей однородной системы уравнений

Представьте двух близких родственниц: неоднородную систему (у которой хотя бы одно число правой части отлично от нуля) и такую же систему– только справа одни нули (то бишь, однородную систему). Нетрудно предположить, что если системы отличаются лишь столбцом свободных членов, то между их решениями должна существовать тесная связь. И это действительно так! Материал целесообразнее рассмотреть на конкретной задаче, которая, как и все другие, взята из реальной контрольной работы:

Пример 5

Дана система линейных алгебраических уравнений

Требуется:

1) найти общее решение;

2) используя результат предыдущего пункта, найти общее решение соответствующей однородной системы и записать его в векторной форме.

Решение: по условию дана обычная неоднородная система уравнений, и первая часть не отличается новизной:

1) Запишем расширенную матрицу системы (не зеваем нолик в третьей строке) и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) Ко второй строке прибавили первую строку, умноженную на –1. К третьей строке прибавили первую строку, умноженную на –3. К четвёртой строке прибавили первую строку, умноженную на –4.

(2) Последние три строки одинаковы, две из них удалили.

Обратным ходом метода Гаусса получим общее решение:
– базисные переменные;
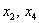– свободные переменные.

Выразим базисные переменные через свободные переменные. Из 2-го уравнения:
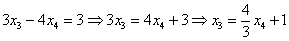– подставим в 1-е уравнение:

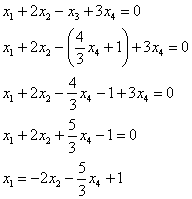
Общее решение неоднородной системы обозначим через 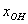(«Общее Неоднородной»).

Ответ: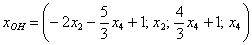

2) Во второй части задания требуется найти общее решение 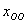такой же, только однородной системы 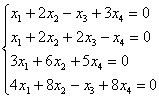, причём по условию необходимо использовать ответ предыдущего пункта.

Выполнять элементарные преобразования заново, разумеется, не нужно.

Правило: общее решение неоднородной системы 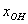равно сумме общего решения соответствующей однородной системы 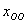и какого-либо частного решения неоднородной системы :

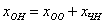
Откуда легко выражается общее решение нашей однородной системы:

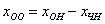
Найдём какое-нибудь частное решение неоднородной системы. Проще всего взять нулевые значения свободных переменных :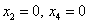

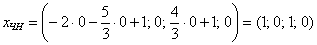
Таким образом, общее решение соответствующей однородной системы:

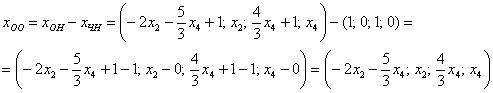
Представим 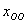в векторной форме. Поскольку у нас две свободные переменные, то фундаментальная система решений будет состоять из двух векторов.

Пойдём классическим путём:

Рассмотрим пару значений свободных переменных 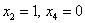и получим первый вектор:
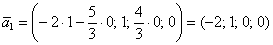– координаты данного вектора удовлетворяют каждому уравнению однородной системы (всегда желательна проверка!).

Теперь рассматриваем пару и получаем второй вектор:
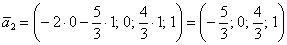– координаты данного вектора также удовлетворяют каждому уравнению однородной системы (тоже проверяем!).

И вообще – любая линейная комбинация векторов фундаментальной системы , где – произвольные действительные числа, является решением данной системы:

Ответ: 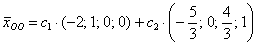, где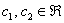

Иными словами, если взять два любых вещественных числа, например, , то получится вектор частного решения однородной системы:
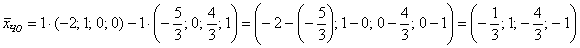, то есть набор удовлетворяет каждому уравнению однородной системы.

Если хотите избежать дробей, то при нахождении вектора 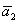следует выбрать значения 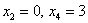и получить второй вектор в виде:

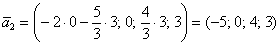
В этом случае ответ запишется в эквивалентной форме:
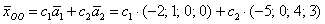, где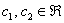

Порядком многих я, наверное, подзапутал, но коль скоро задание не придумано, то его нельзя было обойти стороной.

Более распространённая тема для самостоятельного решения:

Пример 6

Дана однородная система

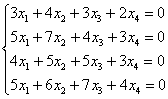
Найти общее решение и записать ответ с помощью векторов фундаментальной системы. В образце решения завершающим элементарным преобразованием я уже потихоньку начинаю приобщать вас к методу Гаусса-Жордана.

Чтобы окончательно закрепить алгоритм, разберём финальное задание:

Пример 7

Решить однородную систему, ответ записать в векторной форме.

Решение: запишем матрицу системы и с помощью элементарных преобразований приведём её к ступенчатому виду:

(1) У первой строки сменили знак. Ещё раз заостряю внимание на неоднократно встречавшемся приёме, который позволяет существенно упростить следующее действие.

(1) Ко 2-й и 3-й строкам прибавили первую строку. К 4-й строке прибавили первую строку, умноженную на 2.

(3) Последние три строки пропорциональны, две из них удалили.

В результате получена стандартная ступенчатая матрица, и решение продолжается по накатанной колее:

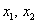– базисные переменные;
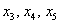– свободные переменные.

Выразим базисные переменные через свободные переменные. Из 2-го уравнения:

– подставим в 1-е уравнение:

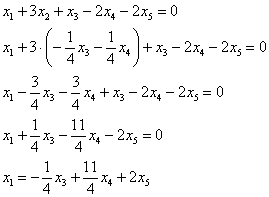
Таким образом, общее решение:

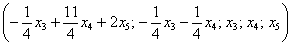
Поскольку в рассматриваемом примере три свободные переменные, то фундаментальная система содержит три вектора.

Подставим тройку значений в общее решение и получим вектор 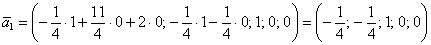, координаты которого удовлетворяют каждому уравнению однородной системы. И снова повторюсь, что крайне желательно проверять каждый полученный вектор – времени займет не так много, а от ошибок убережёт стопроцентно.

Для тройки значений 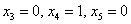находим вектор

И, наконец, для тройки получаем третий вектор:

Ответ: 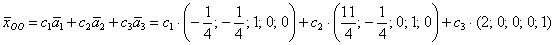, где

Желающие избежать дробных значений могут рассмотреть тройки 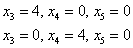и получить ответ в эквивалентном виде:

К слову о дробях. Посмотрим на полученную в задаче матрицу 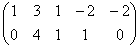и зададимся вопросом – нельзя ли упростить дальнейшее решение? Ведь здесь мы сначала выразили через дроби базисную переменную , потом через дроби базисную переменную , и, надо сказать, процесс это был не самый простой и не самый приятный.

Второй вариант решения:

Идея состоит в том, чтобы попытаться выбрать другие базисные переменные. Посмотрим на матрицу и заметим две единицы в третьем столбце. Так почему бы не получить ноль вверху? Проведём ещё одно элементарное преобразование:

(4) К первой строке прибавили вторую строку, умноженную на –1.

Здесь базисные переменные легко и практически мгновенно выражаются через свободные переменные :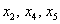

По существу, мы применили метод Гаусса-Жордана, который как раз и направлен на скорейшее получение базисного решения посредством дополнительных элементарных преобразований.

В результате общее решение: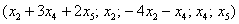

Последовательно выбираем в качестве значений свободных неизвестных тройки

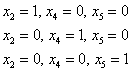
и подстановкой их в 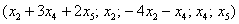получаем соответствующие векторы фундаментальной системы:

Не забываем проверить координаты каждого вектора!

Ответ: общее решение:

2 Приведение квадратичной формы к нормальному виду. Метод Лагранжа.

http://sci.alnam.ru/book_alin.php?id=36

http://spargalki.ru/mathematiks/210-lineinaya-algebra.html?start=9

Постановка задачи. Привести квадратичную форму

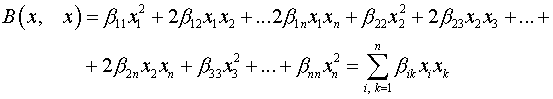
к каноническому виду методом Лагранжа.

План решения.

Метод Лагранжа заключается в последовательном выделении полных квадратов. Не ограничивая общности рассуждений, полагаем, что .

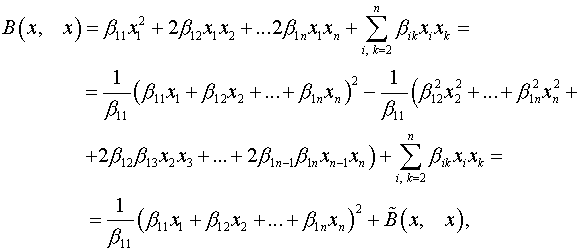
где 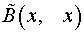– квадратичная форма, в которую входят лишь переменные .

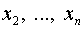Делаем замену

,

после которой

,

где .

Предложенный алгоритм применяем к 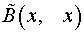и после конечного числа шагов приходим к каноническому виду квадратичной формы:

.

Задача 10. Привести квадратичную форму к каноническому виду методом Лагранжа

.

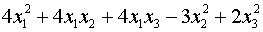Применяя метод Лагранжа, получаем:

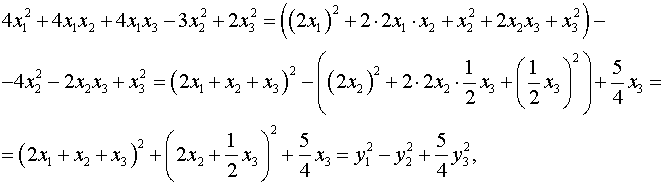
где .

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 8

1. Общее решение неоднородной системы линейных уравнений.

http://matworld.ru/calculator/non-homogeneous-system-online.php

http://www.cleverstudents.ru/systems/solving_systems_of_linear_equations.html#fundamental_system_of_solutions

2. Критерий Сильвестра положительной определенности квадратичной формы.

http://www.studfiles.ru/preview/3072512/page:4/

Критерий Сильвестра

Тип квадратичной формы можно определить, не приводя ее к каноническому виду. Следующий ниже критерий Сильвестра позволяет определить тип квадратичной формы по знакам угловых миноров ее матрицы.

Рассмотрим угловые миноры ( ), являющиеся определителями подматриц 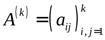матрицы квадратичной формы:

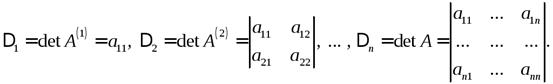
Теорема 6(критерий Сильвестра знакоопределенности квадратичной формы).Квадратичная форма является:

1) положительно определенной тогда и только тогда, когда все угловые миноры матрицы положительны:

( )

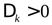2) отрицательно определенной тогда и только тогда, когда все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус:

В заключение приведем таблицу оценки знакоопределенности квадратичных форм по двум основным критериям.

Квадратичная форма	Обозна- чение	Оценка знакоопределенности формы
по главным минорам матрицы квадратичной формы	по собственным значениям матрицы квадратичной формы
положительно определенная		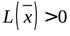если все угловые миноры матрицы положительны: 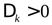( )	если все собственные значения положительны
отрицательно определенная		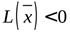если все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус:	если все собственные значения отрицательны
неотрицательно определенная		если все угловые миноры матрицы неотрицательны: 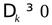( )	если все собственные значения неотрицательны
неположительно определенная		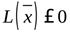если в угловых минорах матрицы чередуются знаки, причем:	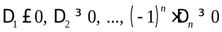если все собственные значения неположительны
знакопеременная			среди собственных значений имеются как положительные, так и отрицательные

Пример 6.Исследовать на знакоопределенность следующие квадратичные формыот двух переменных

, ,

, .

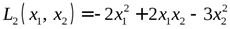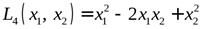Решение.

1) Матрица формы имеет вид

.

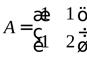Ее угловые миноры равны

, .

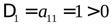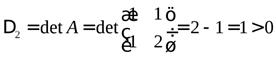Согласно критерию Сильвестра, так как все угловые миноры положительны, квадратичная форма 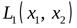являетсяположительно определенной.

2) Матрица формы 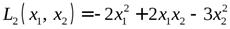имеет вид

.

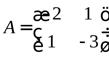Ее угловые миноры равны

, .

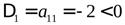Согласно критерию Сильвестра, так как все угловые миноры матрицы отличны от нуля и их знаки чередуются, начиная со знака минус, то квадратичная форма являетсяотрицательно определенной.

3) Матрица формы 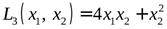имеет вид

.

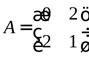Ее угловые миноры равны

, .

Так как в этом случае второй угловой минор отрицателен, то согласно таблице квадратичная форма являетсязнакопеременной.

4) Матрица формы 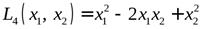имеет вид

.

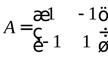Ее угловые миноры равны

, .

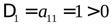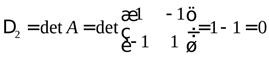Так первый угловой минор положителен, а второй угловой минор равен нулю, то согласно таблице квадратичная форма являетсянеотрицательно определенной.

Заметим, что в данном случае

.

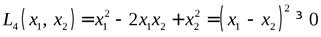Пример 7.Исследовать на знакоопределенность квадратичную формуот трех переменных

.

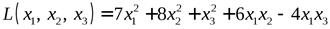Решение.Матрица формы имеет вид

.

Ее угловые миноры положительны:

, , .

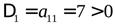Согласно критерию Сильвестра, так как все угловые миноры положительны, то квадратичная форма является положительно определенной.

ЭКЗАМЕНАЦИОННЫЙ БИЛЕТ № 9

1. Линейные пространства. Базис. Размерность.

http://mathhelpplanet.com/static.php?p=razmernost-i-bazis-linyeinogo-prostranstva

Линейное пространство

VV

называется n-мерным, если в нем существует система из

nn

линейно независимых векторов, а любая система из большего количества векторов линейно зависима. Число

nn

называется размерностью (числом измерений) линейного пространства

VV

и обозначается

dimVdim⁡V

. Другими словами, размерность пространства — это максимальное число линейно независимых векторов этого пространства. Если такое число существует, то пространство называется конечномерным. Если же для любого натурального числа п в пространстве

VV

найдется система, состоящая из

nn

линейно независимых векторов, то такое пространство называют бесконечномерным (записывают:

dimV=∞dim⁡V=∞

). Далее, если не оговорено противное, будут рассматриваться конечномерные пространства.

Базисом n-мерного линейного пространства называется упорядоченная совокупность

nn

линейно независимых векторов (базисных векторов).

2 Преобразование матрицы билинейной формы при смене базиса.

http://www.studfiles.ru/preview/5826382/page:8/