Способы представления отношений
Многие задачи математики, техники и других областей человеческой деятельности получают удобную интерпретацию на языке теории отношений. Все арифметические операции это по существу некоторые отношения между числовыми множествами. Множество отдельных деталей остается складским имуществом до тех пор, пока между ними не реализуются определенные отношения, преобразующие эти детали в какой-нибудь механизм или устройство (телевизор, станок, здания и т.п.) разнообразные отношения складываются между людьми – родители и дети, начальники и подчиненные, преподаватели и студенты.
Отношение между элементами двух множеств, т.е. бинарное отношение устанавливает соответствие элементов одного множества X элементам другого множества Y. Ясно, что такое отношение может быть задано некоторой совокупностью упорядоченных пар 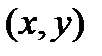 , которые являются элементами множества
, которые являются элементами множества 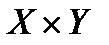 . Это вовсе не значит, что всегда нужно перечислять все такие пары. Часто отношение задается некоторым свойством, выраженным в словесной или символической форме.
. Это вовсе не значит, что всегда нужно перечислять все такие пары. Часто отношение задается некоторым свойством, выраженным в словесной или символической форме.
Если А – отношение, то соотношение 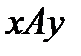 можно записать также в виде
можно записать также в виде 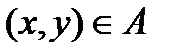 , где
, где 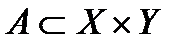 . Например, выражение 3 < 7 и (3, 7)
. Например, выражение 3 < 7 и (3, 7) 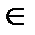 < обозначают одно и тоже, но первые из них привычнее. В то же время (7, 3)
< обозначают одно и тоже, но первые из них привычнее. В то же время (7, 3) 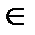 < означало бы 7 < 3, что неверно. Таким образом, в общем случае переставлять элементы в паре
< означало бы 7 < 3, что неверно. Таким образом, в общем случае переставлять элементы в паре 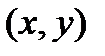 нельзя, что и подчеркивается названием этой пары – упорядоченной. Элемент x называют первой координатой, а элемент y – второй координатой пары.
нельзя, что и подчеркивается названием этой пары – упорядоченной. Элемент x называют первой координатой, а элемент y – второй координатой пары.
Множество первых координат x является областью определения (левой областью) 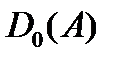 , а множество вторых координат – областью значений (правой областью)
, а множество вторых координат – областью значений (правой областью) 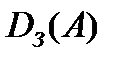 отношения А. Если
отношения А. Если 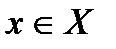 и
и 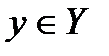 , то
, то 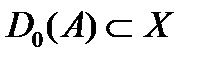 и
и 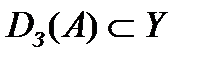 . В таких случаях говорят, что А есть отношение от X к Y. Его также называют соответствием и обозначают
. В таких случаях говорят, что А есть отношение от X к Y. Его также называют соответствием и обозначают 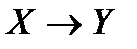 . Если Y=X, то любые отношения
. Если Y=X, то любые отношения 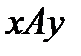 является подмножеством множества
является подмножеством множества 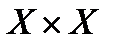 и называется соотношением на X.
и называется соотношением на X.
Пример: 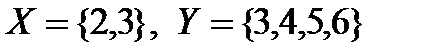 . Произведение этих множеств
. Произведение этих множеств 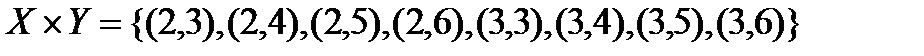 .
.
Отношение «быть делителем» на этих множествах есть множество 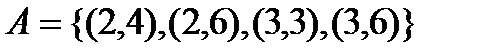 , отношение «равно» есть множество
, отношение «равно» есть множество 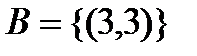 , а отношение «больше» есть пустое множество
, а отношение «больше» есть пустое множество 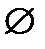 . Области определения и значений отношения А – это соответственно множества
. Области определения и значений отношения А – это соответственно множества 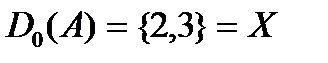 и
и 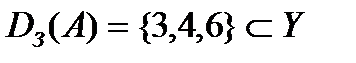 .
.
Если область определения отношения совпадает с некоторым множеством X, то говорят, что отношение определено на X. Подобный случай имеет место в приведенном выше примере отношения А «быть делителем».
Отношения также могут быть установлены между элементами одного и того же множества X , тогда отношение АÌХ×Х.
Для таких отношений различают три частных случая.
1) полное (универсальное) отношение 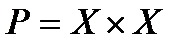 , которое имеет место для каждой пары
, которое имеет место для каждой пары 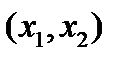 элементов из X (например, отношение «учится в одной группе» на множестве студентов учебной группы);
элементов из X (например, отношение «учится в одной группе» на множестве студентов учебной группы);
2) тождественное (диагональное) отношение Е, которое выполняется между элементом и им самим 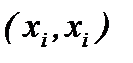 ((например, равенство на множестве действительных чисел x=x);
((например, равенство на множестве действительных чисел x=x);
3) пустое отношение,которому не удовлетворяет ни одна пара элементов из X (например, отношение «быть братом» на множестве женщин).
Формы представления отношений
1. В виде фактор-множества
Рассмотрим отношение 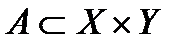 ; если
; если 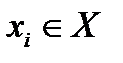 , то сечение по
, то сечение по 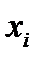 отношения А, обозначаемое
отношения А, обозначаемое 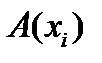 , есть множество
, есть множество 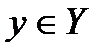 таких, что
таких, что 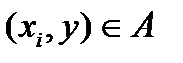 . Множество всех сечений отношения А называют фактор-множеством множества Y по отношению А и обозначают Y/A. Оно полностью определяет отношение A.
. Множество всех сечений отношения А называют фактор-множеством множества Y по отношению А и обозначают Y/A. Оно полностью определяет отношение A.
Пример: На множествах 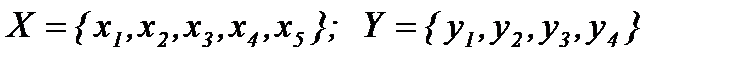 задано бинарное отношение:
задано бинарное отношение:
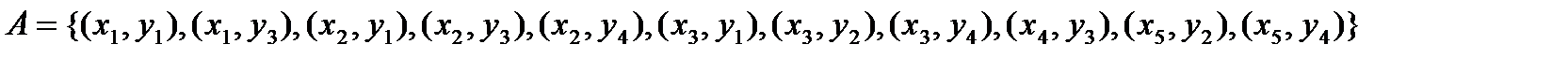 Очевидно,
Очевидно, 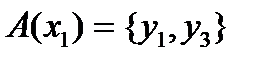 ;
; 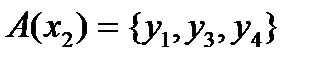 и т.п. Если под каждым элементом из X записать соответствующее сечение отношения A, то элементы второй строки образуют фактор-множество
и т.п. Если под каждым элементом из X записать соответствующее сечение отношения A, то элементы второй строки образуют фактор-множество
Y/A= 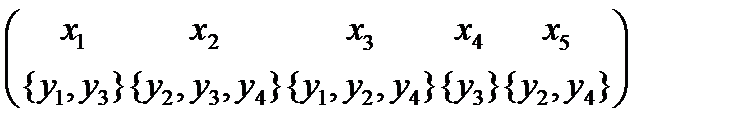 .
.
Объединение сечений по элементам некоторого подмножества 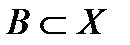 является сечением
является сечением 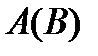 этого подмножества, т.е.
этого подмножества, т.е. 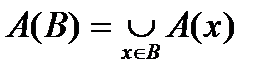 . Так,
. Так,
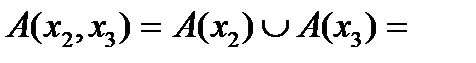
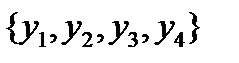
2. Матрица отношений
Строки матрицы соответствуют первым координатам, а столбцы – вторым координатам. На пересечении i-й строки и j-го столбца ставится единица, если выполнено соотношение 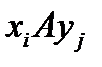 и нуль, если это соотношение не выполняется (иногда нулевые клетки остаются пустыми).
и нуль, если это соотношение не выполняется (иногда нулевые клетки остаются пустыми).
Для предыдущего отношения А
y1 y2 y3 y4
x1
x2
x3
x4
x5
Полному отношению соответствует матрица, все клетки которой заполнены единицами, тождественному – единичная матрица, а пустому – нулевая матрица.
3. Граф отношения.
Вершины графа соответствуют элементам множеств X и Y, а дуга, направленная из вершины 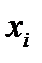 к
к 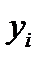 , означает, что
, означает, что 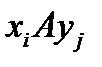 .
.
| x1 |
| x2 |
| x3 |
| x4 |
| x5 |
| y1 |
| y2 |
| y3 |
| y4 |
Рисунок 1.12 – Граф отношения
Отношение в X отображается графом с вершинами, соответствующими элементами этого множества
Если имеют место соотношения 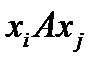 и
и 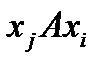 то вершины связываются двумя противоположно направленными дугами, которые можно условно заменять одной ненаправленной дугой. Соотношению
то вершины связываются двумя противоположно направленными дугами, которые можно условно заменять одной ненаправленной дугой. Соотношению 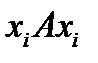 соответствует петля, выходящая из xi и входящая в эту же вершину.
соответствует петля, выходящая из xi и входящая в эту же вершину.
Операции над отношениями
Т.к. отношение – это множества, то над ними можно выполнять все теоретико-множественные операции как и над обычными множествами. Кроме этого для отношений существуют специфические операции: обращение (симметризация) и композиция.
Отношение, симметричное (обратное) некоторому отношению 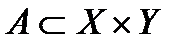 , обозначается через
, обозначается через 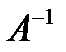 и представляет собой подмножество множества
и представляет собой подмножество множества 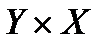 , образованное теми парами
, образованное теми парами 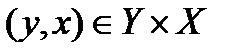 , для которых
, для которых 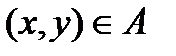 . Переход от А к
. Переход от А к 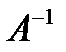 осуществляется взаимной перестановкой координат местами каждой упорядоченной пары. Так, обратное отношение для «x есть делитель y» будет «y делится на x» и для приведенного примера выполняется множеством
осуществляется взаимной перестановкой координат местами каждой упорядоченной пары. Так, обратное отношение для «x есть делитель y» будет «y делится на x» и для приведенного примера выполняется множеством 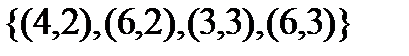 .
.
При переходе от А к 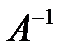 область определения становится областью значений, и наоборот. Матрица обратного отношения получается транспонированием исходной матрицы. Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.
область определения становится областью значений, и наоборот. Матрица обратного отношения получается транспонированием исходной матрицы. Граф обратного отношения находится из исходного графа заменой направлений всех дуг на противоположные.
Композиция отношений 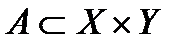 и
и 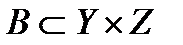 есть отношение С, состоящее из всех тех пар
есть отношение С, состоящее из всех тех пар 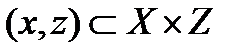 , для которых существует такое
, для которых существует такое 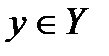 , что
, что 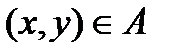 и
и 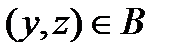 .
.
Сечение отношения С по x совпадает с сечением отношения B по подмножеству 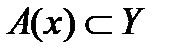 , т.е.
, т.е. 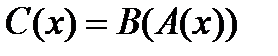 .
.
Рассмотрим, например, два отношения: 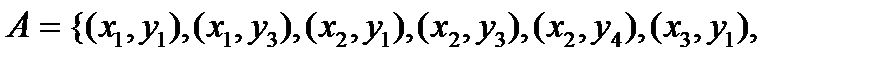
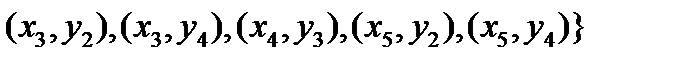 .
. 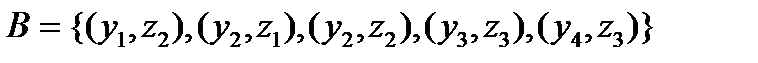 .
.
Очевидно, 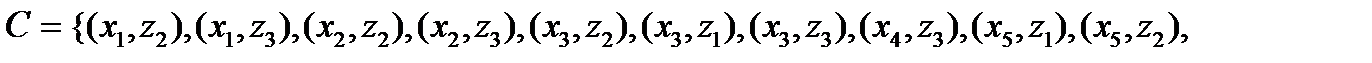
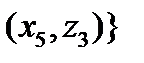 . Сечение
. Сечение 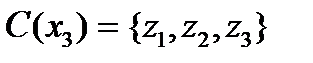 . С другой стороны,
. С другой стороны, 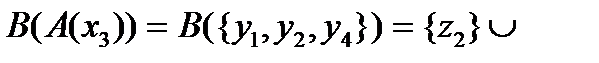
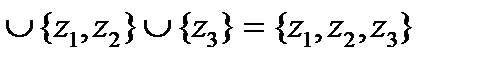 .
.
Композицию С отношений А и B обычно записывают как 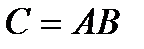 (или
(или 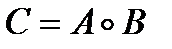 ), тогда
), тогда 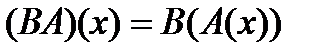 .
.
Композиция отношений обладает ассоциативным законом 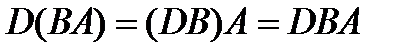 , но не коммутативна
, но не коммутативна 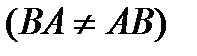 . Можно показать , что
. Можно показать , что 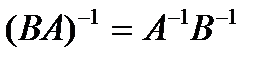 . Композиция отношений
. Композиция отношений 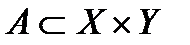 и
и 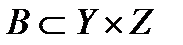 наглядно представляется с помощью графов.
наглядно представляется с помощью графов.
Прежде всего необходимо к графу отношения А добавить граф отношения В. Граф отношения 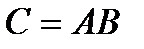 получим, исключив вершины, соответствующие элементам множества Y. При исключении вершины
получим, исключив вершины, соответствующие элементам множества Y. При исключении вершины 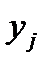 каждый проходящий через нее путь от вершины x к вершине z заменяется одной дугой с тем же направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам в С и рассматриваются как одна ветвь.
каждый проходящий через нее путь от вершины x к вершине z заменяется одной дугой с тем же направлением. Параллельные ветви с одинаковыми направлениями соответствуют одинаковым парам в С и рассматриваются как одна ветвь.
Аналогично можно получить матрицу композиции 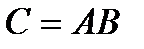 как произведение матриц отношений A и B, которое выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.
как произведение матриц отношений A и B, которое выполняется по обычному правилу умножения прямоугольных матриц с последующей заменой отличного от нуля элемента результирующей матрицы единицей.
Свойства отношений
Пусть А – бинарное отношение в множестве X. Определим общие свойства таких отношений, которые должны выполняться для всех 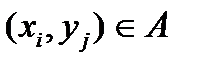 . Говорят, что
. Говорят, что 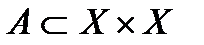 :
:
Рефлексивно, если 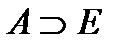 (Е – тождественное отношение), т.е. оно всегда выполняется между объектом и им самим:
(Е – тождественное отношение), т.е. оно всегда выполняется между объектом и им самим: 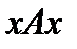 . Этому отношению принадлежат все пары
. Этому отношению принадлежат все пары 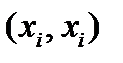 , т.е. пары, в которых отношения «быть делителем на множестве N, т.к. каждое число из N является делителем самого себя. На графе свойство рефлексивности отображается петлей у каждой ветви.
, т.е. пары, в которых отношения «быть делителем на множестве N, т.к. каждое число из N является делителем самого себя. На графе свойство рефлексивности отображается петлей у каждой ветви.
Антирефлексивно, если 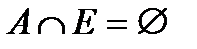 , т.е. может выполняться только для несовпадающих объектов: из
, т.е. может выполняться только для несовпадающих объектов: из 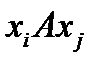 следует
следует 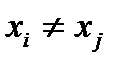 .
.
Свойство симметричности, если 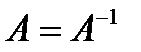 , т.е. при выполнении соотношения
, т.е. при выполнении соотношения 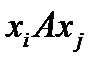 выполняется и соотношение
выполняется и соотношение 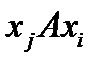 («быть родственником»).
(«быть родственником»).
Свойство асимметричности, если 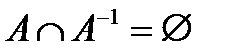 , т.е. из двух соотношений
, т.е. из двух соотношений 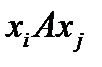 и
и 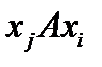 по меньшей мере одно не выполняется; если отношение асимметрично, то оно и антирефлексно.
по меньшей мере одно не выполняется; если отношение асимметрично, то оно и антирефлексно.
Свойство антисимметричности, если 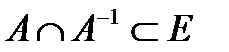 , т.е. оба соотношения
, т.е. оба соотношения 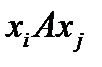 и
и 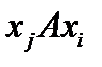 выполняются одновременно только тогда, когда
выполняются одновременно только тогда, когда 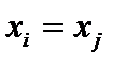 (нестрогое неравенство
(нестрогое неравенство 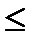 ; включение)
; включение)
Свойство транзитивности, если 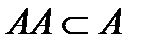 , т.е. из
, т.е. из 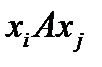 и
и 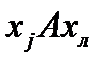 («быть делителем», «быть родственником»), т.е. если элемент x находясь в отношении с элементом y и элемент y находится в отношении A с элементом z, то элемент x находится в отношении A с элементом z.
(«быть делителем», «быть родственником»), т.е. если элемент x находясь в отношении с элементом y и элемент y находится в отношении A с элементом z, то элемент x находится в отношении A с элементом z. 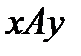 и
и 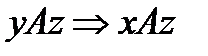 .
.
Для рефлексивного отношения все элементы матрицы на главной диагонали – единицы, а для антирефлексивного – нули. Симметричность отношения влечет и симметричность матрицы, асимметричность отношения – несимметричность матрицы с нулевыми элементами на главной диагонали, антисимметричность отношения – только несимметричность матриц. В матрице транзитивного отношения для каждой пары единичных элементов, один из которых расположен в i-м столбце и j-й строке, а другой в j-м столбце и k-й строке, обязательно существует единичный элемент, расположенный в клетке на пересечении i-го столбца и k-й строки.
