Лекция Множества и их спецификации

1. Способы задания множеств.

2. Операции над множествами.

3. Основные законы и аксиомы алгебры множеств.

4. Круги Эйлера и диаграммы Венна.

5. Решение уравнений с множествами.

1. Способы задания множеств

В повседневной жизни и практической деятельности часто приходится говорить о некоторых совокупностях различных объектов: предметов, понятий, чисел, символов и т.п. Например: совокупность деталей механизмов, аксиом геометрии, чисел натурального ряда, букв русского алфавита. На основе интуитивных представлений о подобных совокупностях сформировалось математическое понятие множества как объединения отдельных объектов в единое целое. Именно такой точки зрения придерживался основатель теории множеств немецкий математик Георг Кантор.

Множество относится к категории наиболее общих, основополагающих понятий математики. Поэтому вместо строгого определения обычно принимается некоторое основное положение о множестве и его элементах. Так группа выдающихся математиков, выступающая под псевдонимом Н. Бурбаки исходит из следующего положения: «Множество образуется из элементов, обладающих некоторыми свойствами и находящихся в некоторых отношениях между собой или элементами других множеств».

Тем не менее, можно сформулировать и более строгое определение множества. Множество – это совокупность отдельных объектов, объединённых в единое целое по некоторому свойству, общему для всех его элементов.

Объекты, составляющие множество, называются его элементами или членами. Множества будем обозначать прописными буквами латинского алфавита, а их элементы – строчными.

A = {a₁, a₂, …, a_n}

Принадлежность элемента к множеству обозначается символом Î

a₁, a₂, …, a_n Î A.

Если а не принадлежит А, то а Ï A или а Î А.

Множество может содержать любое число элементов – конечное или бесконечное и даже не содержать ни одного элемента (пустое множество Æ).

Для конечного множества А число его элементов называют мощностью множества.

Два множества А и В равны (тождественны) А = В, тогда, когда каждый элемент А является элементом В и наоборот. Если не равны множества, то это записывают так А¹В.

Существует два основных способа задания множеств: перечисление и описание.

Перечислением легко задавать конечные множества с небольшим числом его элементов, например:

А = {1, 2, 3, 4, 5, 6, 7, 8, 9, 10}.

Другой способ задания множеств состоит в описании его элементов определяющим свойством P(x) общим для всех элементов. Объективно P(x) – либо одноместная высказывательная форма, либо математическое выражение, где x – переменная, областью значений которой является множество A, тогда P(x) – функция переменной х. Обозначается это так.

{x Î A|P(x)}

Множество тех элементов а Î А для которых высказывание P(a) истинно. Иначе может записываться так x = {x|P(x)}или x = {x : P(x)}. Например {x|x² = 2} – множество чисел, квадрат которых равен двум.

{x|x есть животное с хоботом} – множество слонов.

Множество А, все элементы которого принадлежат и множеству В, называется подмножеством (частью) множества В. Это отношение между множествами называют включением и обозначают символом Ì, т.е. А Ì В (А включает В) или ВÌ А (В включает А). Например: множество положительных чисел – это подмножество множества действительных чисел.

Отношение АÌВ допускает и тождественность А=В, т.е. любое множество можно рассматривать как подмножество самого себя. АÌА. Полагают также, что Æ Ì А. Одновременно выполнение соотношений А Ì В и В Ì А возможно только при А = В. Иногда записывают так А Í В. В этом случае под А Ì В понимают такое отношение включения, которое не допускает равенства А и В (строгое включение), а под А Í В понимают возможность равенства А = В (нестрогое включение).

Любое непустое множество А имеет, по крайней мере, два различных подмножества: само А и пустое множество Æ. Эти подмножества называются несобственными, а все другие подмножества A называются собственными. Конечные собственные подмножества образуются всевозможными сочетаниями по одному, по два, по три и т.п. элементов данного множества.

Множество, элементами которого являются все подмножества множества А называется множеством подмножеств (множеством-степенью) и обозначают P(А).

Для трехэлементного множества А = {a, b, c}

P(A) = {Æ, {a}, {b}, {c}, {a,b}, {b,c}, {a,c}, {a,b,c}}.

В случае конечного множества А, состоящего из n элементов, множество подмножеств P(A) содержит 2ⁿ подмножеств.

Следует подчеркнуть различие между отношением принадлежности и отношением включения. Например множество А = {1, {2, 3}, 4} в числе своих элементов содержит множество {2, 3}, поэтому можно записать: 2, 3 Î {2, 3} и {2, 3} Î A.

Но из этого не следует, что элементы 2 и 3 содержатся в А 2, 3 Ï А.

При определении конкретного множества явно или неявно ограничивается совместимость допустимых объектов. Так множество городов страны следует искать среди населенных пунктов страны, а не среди млекопитающих или целых положительных чисел. Целесообразно совокупность допустимых объектов зафиксировать явным образом и считать, что рассматриваемые множества являются подмножествами этой совместимости. Эту совместимость называют основным множеством (универсумом) и обычно обозначают U. Так универсумом арифметически служат числа, зоологии – мир животных и т.п.

При записи теоретико-множественных соотношений помимо рассмотренных символов используется ряд символов из математической логики: отрицания 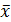(читается «не» или «неверно что»), дизъюнкция Ú (читается «или») конъюнкции Ù (читается «и»), импликации ® (читается «если…, то…»), эквивалентности Û (читается «эквивалентно» или «тогда и только тогда»), квантора всеобщности " (читается «для всех»), квантора существования $ (читается «существует»).

Операции над множествами

Рассмотрим некоторые способы получения новых множеств из имеющихся. Эти способы называются операциями над множествами.

Пусть имеются два множества А и В.

Объединением (соединением, суммой) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат А или В, т.е.

А È В = {x|x Î A или x Î B}

Здесь подразумевается не исключающий смысл слова «или». Т.о., по определению x Î AÈB тогда и только тогда, когда x есть элемент хотя бы одного из множеств А и В.

Например:

{1, 2, 3}È{1, 3, 4} = {1, 2, 3, 4}

Пересечением (произведением) множеств А и В называется множество, состоящее из всех тех и только тех элементов, которые принадлежат каждому из множеств А и В, т.е.

А Ç В = {x|(xÎA) Ç (xÎB)}

Например:

{1, 2, 3} Ç {2, 3, 4,} = {2, 3}

Множества, не имеющие общих элементов АÇВ=Æ, называют непересекающимися (расчлененными).

Разность А\В (или А – В) есть множество, состоящее из всех элементов А, не входящих в В, например, {1, 2, 3}\ {2, 3, 4} = {1}. Разность можно рассмотреть как относительное дополнение В до А. Если АÌU, то множество U\A называется абсолютным дополнением множества А и обозначается через 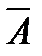. Оно содержит все элементы универсума U, кроме элементов множества А. Дополнение А определяется отрицанием свойства P(x) с помощью которого определяется А. Очевидно,

А\В = А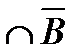

Дизъюнктивная сумма (симметрическая разность) А + В (или А Å В) есть множество всех элементов, принадлежащих или А, или В (но не обоим вместе). Например: {1, 2, 3} Å {2, 3, 4} = {1, 4}.

Дизъюнктивная сумма получается объединением элементов множеств за исключением тех, которые встречаются дважды.

Произведение множеств (декартово произведение) А´В есть множество всех упорядоченных пар элементов (а, b), из которых первый а принадлежит множеству А, а второй b – множеству В.

Например: А = {a₁, a₂, a₃, a₄} и B = {b₁, b₂}.

Тогда А ´ В = {(a₁, b₁), (a₁, b₂), (a₂, b₁), (a₂, b₂), (a₃, b₁), (a₃, b₂), (a₄, b₁), (a₄, b₂)}.

Порядок следования пар может быть любым, но расположение элементов в каждой паре определяется порядком следования перемножаемых множеств. Поэтому В ´ А ¹ А ´ В, если А ¹ В. Указанные операции над множествами обобщаются на любое их количество А₁, А₂, …, А_n. Так, в частности операция произведения множеств записывается

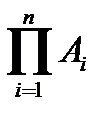= A₁ ´ A₂ ´ … ´ A_n.

В результате получаем множество упорядоченных совокупностей (a₁, a₂, …, a_n), для которых употребляется название: кортеж, последовательность, вектор или просто n-ка, часть для того, чтобы отразить строго определенный порядок следования элементов n-ки записывают <a₁, a₂, …, a_n>.

В частности, если A₁=A₂=…=A_n=A, декартово произведение называется n–кратным или декартовой n-й степенью и обозначается Аⁿ.