Графическое изображение структурных средних величин.
Средняя хронологическая.
Разновидностью средней арифметической является средняя хронологическая.
Средняя хронологическая —это средний уровень ряда динамики, т. е. средняя, исчисленная по совокупности значений показателя в разные моменты или периоды времени. В зависимости от вида ряда динамики применяются различные способы ее расчета, а именно расчет средней хронологической интервального; ряда и средней хронологической моментного ряда.
Средней хронологической интервального рядаявляется средняя величина из уровней интервального ряда динамики, которая исчисляется по формуле
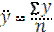 Добавить пр-р!!!!
Добавить пр-р!!!!
где 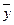 — средний уровень ряда;
— средний уровень ряда;
у — уровень ряда динамики;
n — число членов ряда.
Средней хронологической моментного рядаявляется средняя величина из уровней моментного ряда динамики.
Если f(t) есть функция, выражающая изменение моментного показателя во времени, то за время (t) от а до b средняя хронологическая моментного ряда равна:
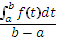
Однако данных непрерывного наблюдения значения f(t) в распоряжении статистики, как правило, нет. Поэтому в зависимости от характера изменения показателя и имеющихся данных применяются различные методы расчета.
При равных промежутках времени между датами, на которые имеются данные, и равномерном изменении размера показателя между датами средняя хронологическая моментного ряда обычно исчисляется по формуле:
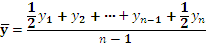
где 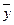 — средний уровень ряда;
— средний уровень ряда;
n — число всех членов ряда;
у —уровень ряда.
Если периоды времени, отделяющие одну дату от другой, не равны между собой, то расчет средней хронологической моментного ряда производится по формуле средней взвешенной арифметической, в качестве весов которой принимаются отрезки времени между датами, т. е. по формуле:
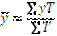
где T— время, в течение которого данный уровень ряда (у) оставался без изменения.
Известно, например, что в январе 2007 года произошло следующее изменение численности сотрудников компании "Бест": было на 1 января 551 чел., уволился 2 января один сотрудник, было принято 6 января 24 человека, 16 января— 6 человек, уволилось 25 января— 10 сотрудников. Требуется определить среднюю численность сотрудников компании "Бест" в январе 2007 г. Рассчитаем число календарных дней, в течение которых численность сотрудников компании "Бест" оставалась без изменения, и произведение этих чисел.
Таблица - Данные для расчета средней численности сотрудников компании "Бест"
| Численность сотрудников компании «Бест», чел. (y) | Число календарных дней, в течении которых данная численность сотрудников оставалась без изменений (Т) | Произведение численности сотрудников на число календарных дней (yТ) |
| ИТОГО |
Используя данные произведенных расчетов, получим:
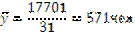
В отличие от первого способа расчета средней хронологической моментного ряда второй способ дает точное значение средней.
ПРИЛОЖЕНИЕ Таблица - Виды средних степенных величин
| Значение, k | Наименование средней | Формула средней | |
| простой | взвешенной | ||
| -1 | Гармоническая | 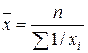 | 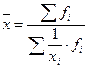 ; ; 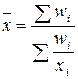 где где 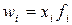 |
| Используется в случае, когда веса равны | Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов | ||
| Геометрическая (после преобразований) | 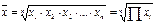 | 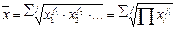 | |
| Используется в анализе динамики для определения среднего темпа роста | |||
| Арифметическая | 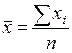 | 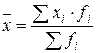 ; ; 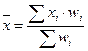 | |
| Используется, когда расчет осуществляется по несгруппированным данным | Используется, когда данные представлены в виде рядов распределения или группировок | ||
| Квадратическая | 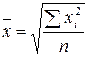 | 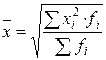 | |
| Используется при расчете показателей вариации. А также если при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п. | |||
| Кубическая | 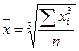 |  | |
| Используется когда необходимо по условиям задачи сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, например, при определении средней длины стороны и кубов |
ПРИЛОЖЕНИЕ Таблица - Виды средних степенных величин
| Значение, k | Наименование средней | Формула средней | |
| простой | взвешенной | ||
| -1 | Гармоническая | 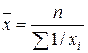 | 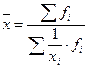 ; ; 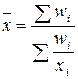 где где 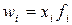 |
| Используется в случае, когда веса равны | Используется, когда известны индивидуальные значения признака и веса W за ряд временных интервалов | ||
| Геометрическая (после преобразований) | 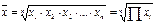 | 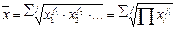 | |
| Используется в анализе динамики для определения среднего темпа роста | |||
| Арифметическая | 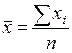 | 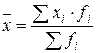 ; ; 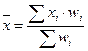 | |
| Используется, когда расчет осуществляется по несгруппированным данным | Используется, когда данные представлены в виде рядов распределения или группировок | ||
| Квадратическая | 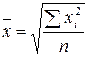 | 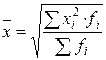 | |
| Используется при расчете показателей вариации. А также если при замене индивидуальных значений признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, например, для вычисления средней величины стороны и квадратных участков, средних диаметров труб, стволов и т.п. | |||
| Кубическая | 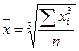 |  | |
| Используется когда необходимо по условиям задачи сохранить неизменной сумму кубов индивидуальных значений признака при их замене на среднюю величину, например, при определении средней длины стороны и кубов |
