Границы применимости решения Эйлера. Формула Ясинского.

Как показали опыты, решение Эйлера подтверждается не во всех случаях. Причина состоит в том, что формула Эйлера была получена в предположении, что при любой нагрузке стержень ра­ботает в пределах упругих деформаций по закону Гука. Следова­тельно, его нельзя применять в тех ситуациях, когда напряжения превосходят предел пропорциональности. В связи с этим найдем границы применимости решения Эйлера:

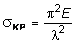. (1)

Из (1) следует, что напряжение s_КР возрастает по мере уменьшения гибкости стержня. Заметим, что стержень, имеющий неодинаковые опорные закрепления в главных плоскостях и, сле­довательно, неодинаковые приведенные длины, теряет устойчи­вость в той главной плоскости, в которой гибкость стержня имеет наибольшее значение.

Формула Эйлера неприемлема, если напряжения s_КР > s_П, где s_П - предел пропорциональности. Приравнивая (1) к пределу пропорциональности, получим предельное значение гибкости:

.

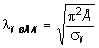Если l > l_ПРЕД. , то формулу Эйлера можно применять. В противном случае ею пользоваться нельзя. Для стали Ст.3 l_ПРЕД = 100.

В ситуациях, когда напряжения превышают предел пропорциональности, получение теоретического решения осложняется, т.к. зависимость между напряжениями и деформациями становится не­линейной. В связи с этим, в этих случаях пользуются эмпириче­скими зависимостями. В частности, Ф.С. Ясинский предложил сле­дующую формулу для критических по устойчивости напряжений:

,

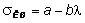где a, b - постоянные, зависящие от материала, так для стали Ст.3 a = 3,1×10⁵ кН/м² , b = 11,4×10² кН/м².

При гибкостях стер­жня, находящихся в диа­пазоне 0< l< 40¸50, стер­жень настолько “коро­ток”, что его разрушение происходит по схеме сжа­тия, следовательно, кри­тические напряжения можно приравнять в этом случае к пределу пропор­циональности. Обобщая вышесказанное, зависи­мость критических на­пряжений s_КР от гибко­сти стержня l можно представить, как это сделано на рис. 1.

Рис.1

Когда формула Эйлера неприменима (за приделом упругости) для определения критической силы можно воспользоваться эмпирической формулой Ясинского П.Ф.:

, ,

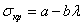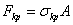здесь 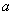и 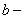коэффициенты, зависящие от материала стержня, измеряются в МПа, приводятся в справочниках: для ст. 3

Сложное сопротивление.

Понятие о сложном сопротивлении, его виды. Изгиб с растяжением. Косой изгиб.

Cложное сопротивление - такие виды нагружения бруса, при которых в поперечных сечениях возникают одновременно не менее двух внутренних силовых факторов.

Случаи сложного сопротивления условно разделяют на два вида. Первый вид составляют случаи сложного сопротивления, при которых в опасных точках бруса напряженное состояние является одноосным. В эту группу объединяют: изгиб с растяжением, косой изгиб, внецентренное растяжение-сжатие и др.

Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:

.

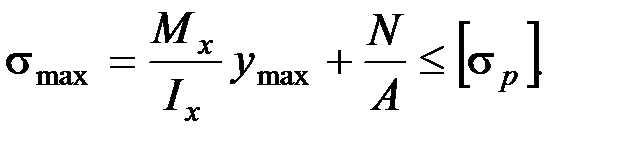Ко второй группе относятся такие случаи сложного сопротивления, когда напряженное состояние является плоским. Например, изгиб с кручением, растяжение(сжатие) с кручением и т.д. Для случая нагружения, относящегося к первой группе, в отличие от второй группы, нет необходимости в применении гипотез прочности.

Косой изгиб проявляется, если прикладываем к балке вертикальную нагрузку, и она при этом изгибается не только в вертикальной плоскости, но и вбок. Косой изгиб - это изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости. Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).

Рассмотрим консольную балку прямоугольного сечения длиной l, нагруженную вертикальной силой P. Главная центральная ось балки (ось симметрии) y составляет некоторый малый угол α с направлением действия нагрузки.

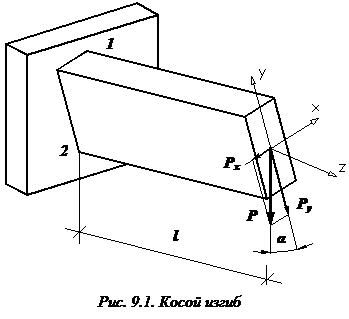
Разложим силу P на составляющие: 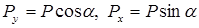. Используя принцип независимости действия сил, рассмотрим отдельно действие каждой составляющей. Нагрузк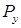и и 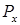вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты:

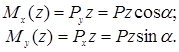
Оба изгибающих момента будут наибольшими в жесткой заделке:

.

Формула суммарных нормальных напряжений при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y:

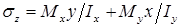, где 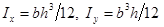– главные моменты инерции; h – высота, а b – ширина прямоугольного поперечного сечения балки. Величины изгибающих моментов и координат данной точки подставляются в формулу нормальных напряжений при косом изгибе, знак каждого из слагаемых определяется по физическому смыслу.

Наибольшие нормальные напряжения при косом изгибе возникнут в поперечном сечении, расположенном в жесткой заделке, в наиболее удаленных от соответствующих нейтральных осейточках 1 и 2:

. В точке 1 напряжения будут растягивающими: 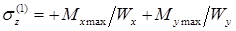, а в точке 2 – такими же по величине, но сжимающими.

В формулах максимальных нормальных напряжений при косом изгибе 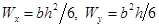– осевые моменты сопротивления балки относительно главных центральных осей инерции.

Нейтральная линия – это геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю.

Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения 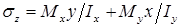к нулю: ,

.

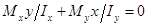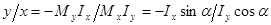При косом изгибе условие прочности имеет вид:

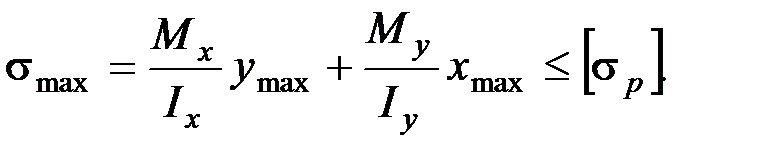
Косой изгиб опасен тем, что при производственном браке (перекосе) могут существенно увеличиться нормальные напряжения в балке.

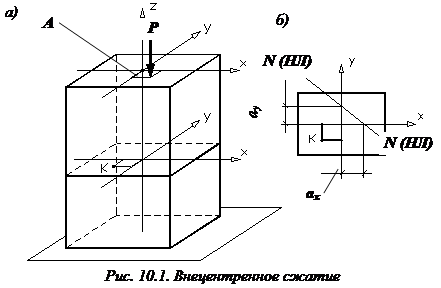
Внецентренное сжатие.

Внецентренное сжатие. Построениеядра сечения. Изгиб с кручением. Расчеты на прочность при сложном напряженном состоянии.

Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При внецентренном сжатии, помимо продольной силы (N), возникают два изгибающих момента ( 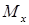и ).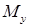

Считают, что стержень обладает большой жесткостью на изгиб, чтобы пренебречь прогибом стержня при внецентренном сжатии.

Преобразуем формулу моментов при внецентренном сжатии , подставляя значения изгибающих моментов: .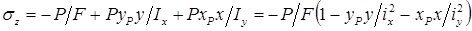

Обозначим координаты некоторой точки нулевой линии при внецентренном сжатии 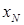, 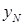и подставим их в формулу нормальных напряжений при внецентренном сжатии. Учитывая, что напряжения в точках нулевой линии равны нулю, после сокращения на 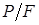, получим уравнение нулевой линии при внецентренном сжатии: .

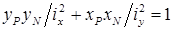Нулевая линия при внецентренном сжатии и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести сечения.

Отрезки, отсекаемые нулевой линией от осей координат, обозначенные 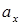и 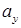, легко найти из уравнения нулевой линии при внецентренном сжатии. Если сначала принять 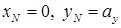, а затем принять 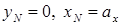, то найдем точки пересечения нулевой линии при внецентренном сжатии с главными центральными осями:

;

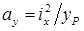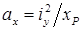
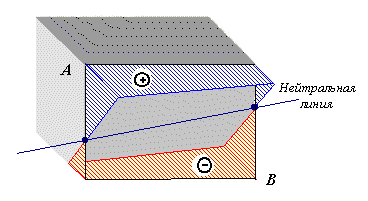
Нулевая линия при внецентренном сжатии разделит поперечное сечение на две части. В одной части напряжения будут сжимающими, в другой – растягивающими. Расчет на прочность, как и в случае косого изгиба, проводят по нормальным напряжениям, возникающим в опасной точке поперечного сечения (наиболее удаленной от нулевой линии).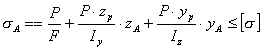

Ядро сечения - малая область вокруг центра тяжести поперечного сечения, характерная тем, что любая сжимающая продольная сила, приложенная внутри ядра, вызывает во всех точках поперечного сечения сжимающие напряжения.

Примеры ядра сечения для прямоугольного и круглого поперечных сечений стержня.

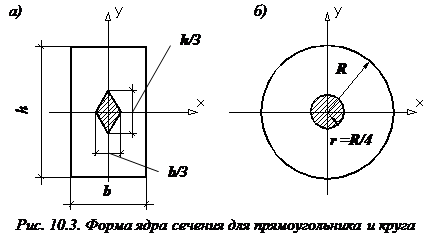
Изгиб с кручением. Такому нагружению (одновременному действию крутящих и изгибающих моментов) часто подвержены валы машин и механизмов. Для расчета бруса необходимо прежде всего установить опасные сечения. Для этого строятся эпюры изгибающих и крутящих моментов.

Рис.1

Используя принцип независимости действия сил, определим напряжения, возникающие в брусе отдельно для кручения, и для изгиба.

При кручении в поперечных сечениях бруса возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения 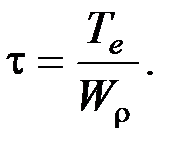При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах бруса .

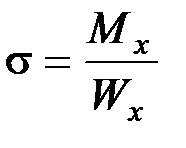Касательные напряжения значительно меньше напряжений от крутящего момента, поэтому ими пренебрегают. Опасное сечение бруса будет у заделки, где действуют максимальные напряжения от изгиба и кручения.

Исследуем напряженное состояние в наиболее опасной точке 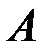(рис. 1). Так как напряженное состояние двухосное, то для проверки прочности применяет одну из гипотез.

Применяя третью теорию прочности 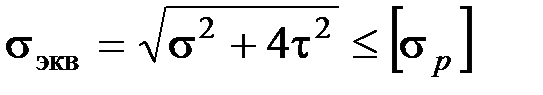и учитывая, что 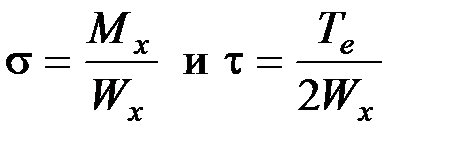, получаем: 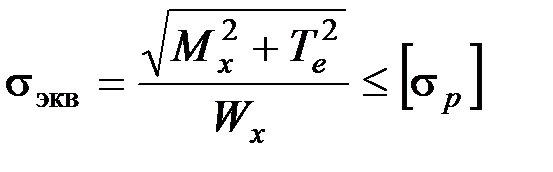. Для подбора сечения находим требуемый момент сопротивления .

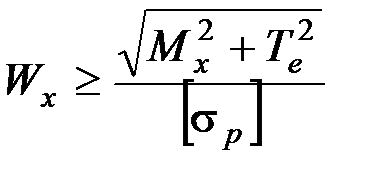Динамические нагрузки.