Лекция 2. Центральное растяжение – сжатие.

Лекция 2. Центральное растяжение – сжатие.

Внутренние силы в поперечных сечениях стержня. Построение эпюр внутренних сил от действия внешних сил. Напряжения в поперечных сечениях стержня. Деформации продольные и поперечные, коэффициент Пуассона. Закон Гука. Модуль упругости. Определение перемещений поперечных сечений стержня. Посторенние эпюр напряжений и перемещений.

Растяжение и сжатие – это наиболее простые и часто встречающиеся виды деформации. На растяжение и сжатие работают многие элементы конструкций: стержни ферм, колонны, канаты лебедок, штоки паровых машин, лонжероны крыла самолетов.

При растяжении или сжатие в поперечных сечениях бруса возникает только один внутренний силовой фактор – внутренняя продольная сила 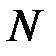(рис. 3). Брус имеет два характерных участка. Для определения продольной силы 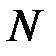воспользуемся методом сечения. На расстоянии 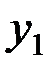проведем сечение на первом участке и рассмотрим равновесие отсеченной части (рис. 4). Продольную силу будем всегда показывать от сечения, что будет соответствовать растяжению бруса.

Составим условие равновесия на ось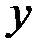

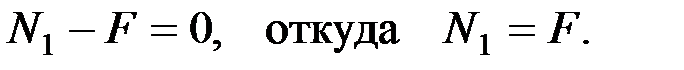
Проведем на втором участке сечение на расстоянии 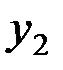. Рассматривая равновесие отсеченной части, получаем 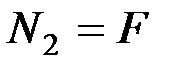. Строим эпюру продольных сил.

Рис. 4

Нормальные напряжения. Исходя из определения напряжения, можно записать

,

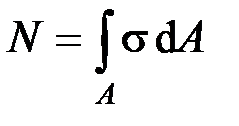где 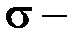нормальное напряжение в произвольной точке сечения.

Согласно гипотезе плоских сечений (гипотеза Бернулли) все продольные волокна бруса деформируются одинаково, а это означает, что напряжения в поперечных сечениях одинаковы, т.е. .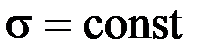

В этом случае получаем

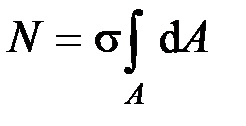, откуда .

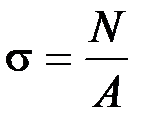Рассчитывая напряжения в каждом сечении, строим эпюру нормальных напряжений (рис.3).

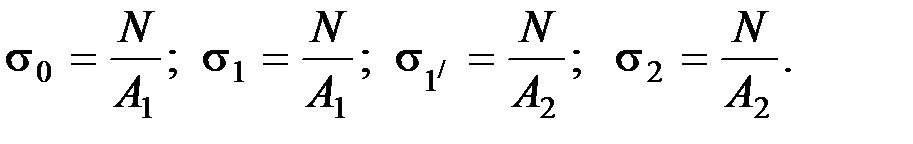
Деформации и перемещения.

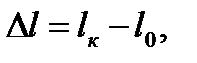Величина, на которую изменится длина бруса (или одного из его участков) под действием продольных сил, называется продольной деформацией (рис.5):

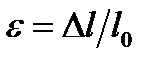Относительной продольной деформацией называется отношение абсолютной продольной деформации Dl к первоначальной длине стержня l:

Величина Dа (Db), на которую изменится размер поперечного сечения бруса а (b) под действием продольной силы, называется поперечной деформацией.

Отношение абсолютной поперечной деформации, Dа (Db) к первоначальному размеру сечения бруса а (b), называется относительной поперечной деформацией:

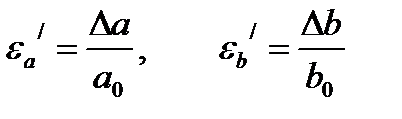
Рис. 5

Лекция 4. Сдвиг (срез).

Понятие чистого сдвига. Элементы конструкций, работающих в условиях чистого сдвига. Деформации, напряжения. Площадки чистого сдвига. Закон Гука при сдвиге. Условие прочности при сдвиге (срезе).

Сдвиг (срез) - вид деформации, при котором одна часть стержня смещается относительно другой (скользит). Сдвиг, как вид нагружения, встречается редко и имеет место в заклепочных и сварных соединениях. Деформация сдвига происходит в случае, если к стержню приложены две равные по модулю противоположно направленные силы P , перпендикулярные к его продольной оси. Расстояние между этими силами должно быть малым, чтобы можно было пренебречь моментом, создаваемым силами.

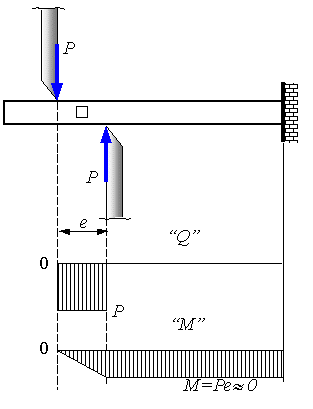
Используя метод сечений (разрезая стержень между силами P), можно установить, что в поперечном сечении стержня возникает только одно внутреннее усилие – поперечная сила Q.

Такой вид нагружения, при котором в поперечных сечениях стержня действует только поперечная сила, называют чистым сдвигом.

Мера скольжения одного поперечного сечения относительно другого - касательные напряжения τ.

Принято, что касательные напряжения распределены по всей площади поперечного сечения равномерно.

Рис.1

Если в поперечном сечении стержня площадью A возникает внутренняя поперечная сила Q=P , то касательные напряжения в любой точке этого сечения будут равны: Τ = Q / A = P / A.

При чистом сдвиге возникает плоское напряженное состояние, тогда напряжения, действующие на площадке составляющей угол 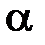с вертикальной исходной площадкой равны:

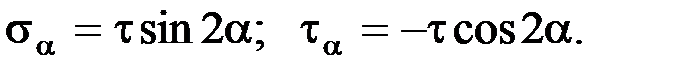
Касательные напряжения τ, приведенные на рис. 1, по абсолютной величине больше касательных напряжений по любым другим площадкам. Таким образом, они являются экстремальными, а площадки, по которым они действуют – площадками сдвига. Так как по этим площадкам не действуют нормальные напряжения, то их называют площадками чистого сдвига и они образуют с главными площадками углы, равные 45⁰.

При чистом сдвиге нормальные напряжения на любых двух взаимно перпендикулярных площадках равны друг другу по модулю и противоположны по направлению.

В результате сдвига одно поперечное сечение стержня смещается относительно другого на величину δ , называемую абсолютным сдвигом.

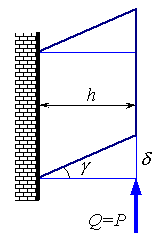
Малый угол γ, на который изменится первоначально прямой угол, – относительный сдвиг, выражается в радианах.

Угол сдвига 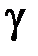пропорционален касательным напряжениям. Математическая зависимость между углом сдвига и касательным напряжением называется законом Гука при сдвиге:

.

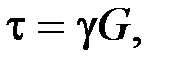Зависимость между модулем сдвига и модулем Юнга:

.

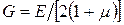Значение коэффициента Пуассона μ находится в пределах 0 ≤ μ ≤ 0,5.

Условие прочности при сдвиге имеет вид:

τ = Q / A ≤ [ τ ]

Кручение.

Крутящие моменты (внутренний силовой фактор) в поперечных сечениях стержня. Кручение стержней круглого поперечного сечения: допущения, деформации, напряжения, углы закручивания. Условия прочности, жёсткости. Построение эпюр крутящих моментов.

Кручение имеет место в случае действия на вал момента (пары сил) относительно его продольной оси, и в поперечных сечениях бруса возникает только один силовой фактор – крутящий момент. Брус, работающий на кручение называется валом. При кручении вала его поперечные сечения поворачиваются друг относительно друга, вращаясь вокруг оси бруса.

Напряжения и деформации при кручении бруса. Под действием внешнего скручивающего момента, приложенного на правом конце бруса, левый конец которого жестко закреплен, брус будет закручиваться. Выделим из бруса элементарный цилиндр длиной 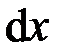. Будем считать, что левое сечение бруса жестко закреплено. Под действием крутящего момента 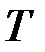правое сечение повернется на некоторый угол .

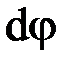Так как 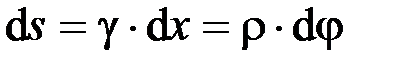, то получаем .

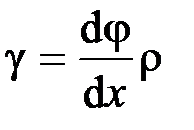Из данной зависимости видно, что угол сдвига 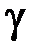изменяется по радиусу вала по линейному закону.

Деформация бруса при кручении характеризуется относительным углом закручивания .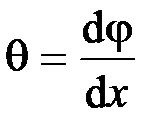

При малых углах закручивания вала в теории кручения круглых стержней принимаются допущения:

1. Поперечные сечения, плоские и перпендикулярные к его оси до деформации, остаются плоскими (не коробятся) и перпендикулярными к оси вала и после деформации (гипотеза Бернулли);

2. Радиусы поперечных сечений при деформации не искривляются и не изменяют своей длины;

3. Длина вала в результате закручивания не изменяется.

Поперечное сечение вала ведет себя при кручении, как жесткий диск, идеформациюкручения можно рассматривать, как результатсдвига одного поперечного сечения относительно другого. В этом случае в точках поперечного сечения вала возникают только касательные напряжения.

Теория кручения, основанная на упомянутых допущениях, подтверждается экспериментальными данными.

Согласно закону Гука при сдвиге, имеем 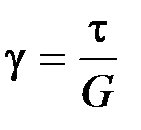. Откуда получаем: .

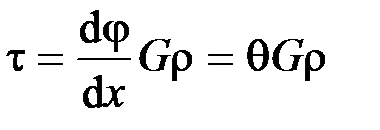Из полученной зависимости следует, что касательные напряжения изменяются по радиусу по линейному закону.

При кручении все внутренние силы, распределенные по поперечному сечению, приводятся к одной составляющей - к крутящему моменту. Крутящий момент 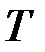в сечении бруса определяется по формуле

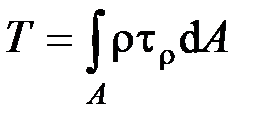, где 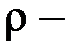плечо элементарной силы.

Подставляя значение касательного ускорения, получим

.

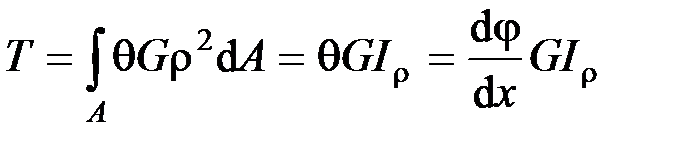Элементарный угол закручивания бруса: 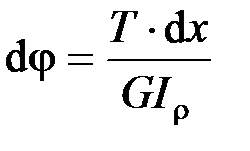; полный угол закручивания .

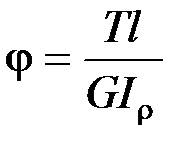Максимальное касательное напряжение в поперечном сечении бруса будет определяться по зависимости:

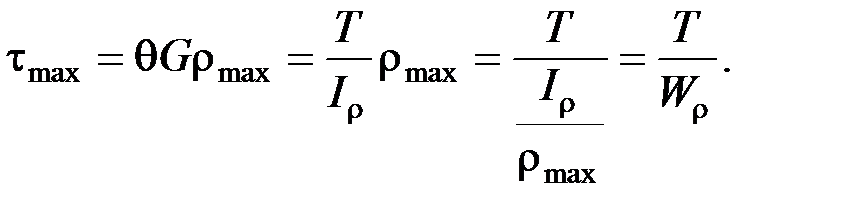
Прочность и жесткость при кручении. Условие прочности при кручении имеет вид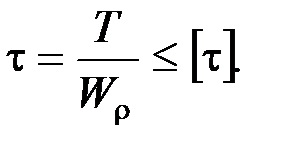

Условие жесткости: .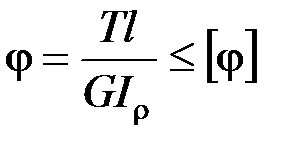

Для бруса круглого сечения эти условия принимают вид:

.

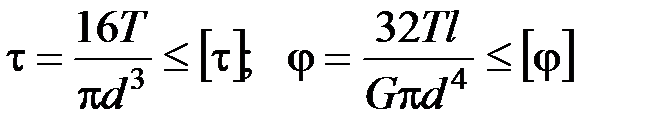Построение эпюр крутящих моментов.Крутящий момент равен алгебраической сумме скручивающих моментов, приложенных к любой из частей стержня. Эпюра крутящих моментов – это график, показывающий изменения крутящего момента по длине вала.

При построении эпюры крутящих моментов используется правило знаков: скручивающий момент, вращающий рассматриваемую часть стержня против хода часовой стрелки при взгляде на поперечное сечение, вызывает в этом сечении положительный крутящий момент.

Брус разбивается на участке, на каждом участке проводится сечение и определяется крутящий момент. Затем строится эпюра крутящих моментов.

Лекция 5. Изгиб.

Плоский поперечный изгиб прямых стержней (брусьев, балок). Определение внутренних сил (поперечных сил и изгибающих моментов) в произвольном поперечном сечении стержня и построение их эпюр. Дифференциальные зависимости между нагрузкой, поперечными силами, изгибающими моментами, их использование при построении диаграмм и контроля правильности построения.

Под плоским поперечным изгибом понимают такой вид деформации, при которой происходит искривление оси прямого бруса, и в поперечном сечении бруса действует два силовых фактора: изгибающий момент М и поперечная сила Q. Осью бруса называется геометрическое место точек центров тяжестей поперечных сечений бруса. Изгиб - плоский, если ось балки после деформации остается плоской линией. В противном случае имеет место косой изгиб. Если поперечная сила не возникает, изгиб называется чистым изгибом.

Рассмотрим, например, балку, нагруженную вертикальной сосредоточенной силой P.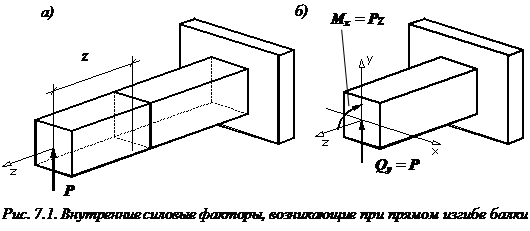

Разрежем мысленно балку в интересующем месте на две части. Отбросим левую часть балки, нагруженную силой P. Заменим действие отброшенной левой части балки на оставленную правую часть внутренними силами.

Внутренние усилия возникают во всех точках поперечного сечения балки и распределены по неизвестному закону. Не имея возможности определить эти внутренние усилия для каждой точки сечения, заменяем их статически эквивалентнымивнутренними силовыми факторами, приложенными в центре тяжести поперечного сечения.

Внутренние силовые факторы определяются из условия равновесия рассматриваемой части балки. Однако можем внутренние силовые факторы найти и непосредственно, как действие отброшенной левой части на правую часть. Видно, что часть балки, нагруженная силой P, стремится изогнуть рассматриваемую нами правую часть выпуклостью вниз, а также пытается произвести срез. Следовательно, в сечении должны возникнуть поперечная сила и изгибающий момент.

Осуществим параллельный перенос силы P в центр тяжести поперечного сечения балки. По правилам теоретической механики добавляется момент, равный .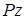

Таким образом, в поперечном сечении балки возникают два внутренних силовых фактора:

изгибающий момент, численно равный алгебраической сумме моментов всех сил, приложенных к отбрасываемой части балки, относительно главной центральной оси, проходящей через центр тяжести рассматриваемого сечения (в данном примере М= Рz);

поперечная сила, численно равная алгебраической сумме всех внешних сил (активных и реактивных), действующих на отбрасываемую часть балки, в нашем примере Q = P).

Построение эпюр поперечных сил и изгибающих моментов. При расчете балок на прочность необходимо знать характер изменения изгибающего момента и поперечной силы вдоль оси балки и знать положение опасного сечения. С этой целью строят эпюры поперечных сил и изгибающих моментов.

Если внешняя сила стремится повернуть отсеченную часть по часовой стрелке относительно рассматриваемого сечения, то поперечная сила положительна.

+Qy

+Mx

Изгибающий момент будет положительным, если при действии момента внешних сил балка искривляется выпуклостью вниз.

Построение эпюр поперечных сил и изгибающих моментов рассмотрим на конкретном примере.

Пусть на балку действует внешний изгибающий момент 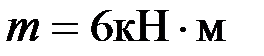и внешняя сила 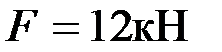, 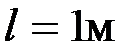. Определим реакции в опорах 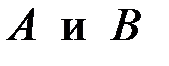. Составим уравнения равновесия моментов всех внешних сил относительно опор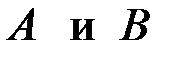

;

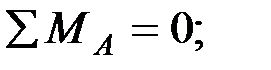
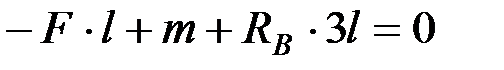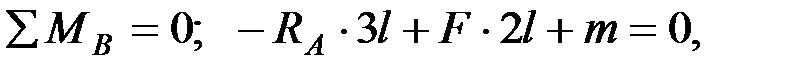
откуда

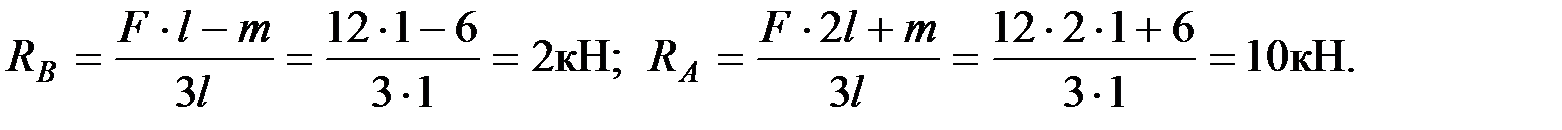
Проведем сечения на каждом характерном участке и определим значения поперечной силы 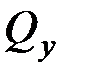и изгибающего момента .

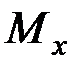В сечении 1

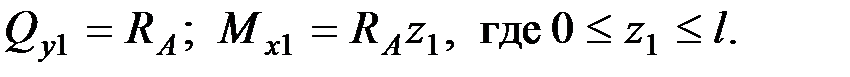
При ;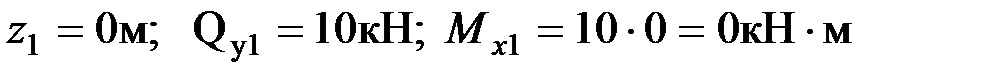

при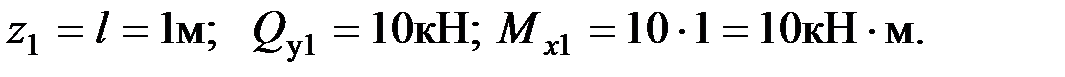

В сечении 2

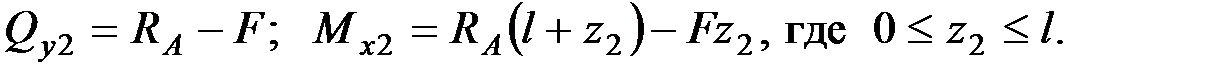
При ;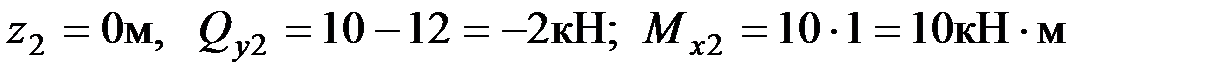

при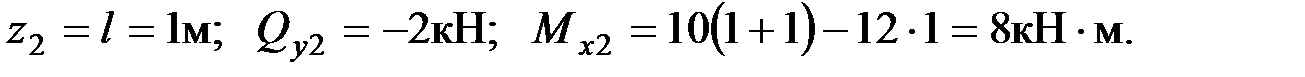

В сечении 3

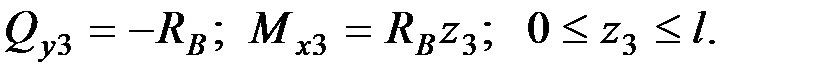
При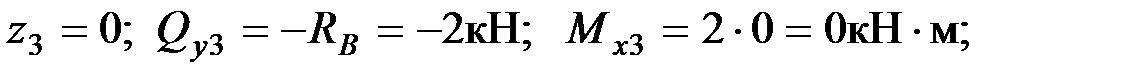

при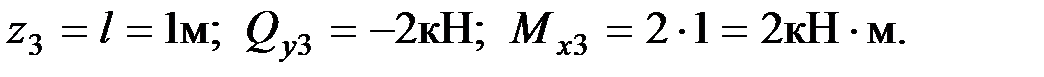

По полученным значениям строим эпюры поперечных сил и изгибающих моментов .

Формула Ясинского.

Сложное сопротивление.

Понятие о сложном сопротивлении, его виды. Изгиб с растяжением. Косой изгиб.

Cложное сопротивление - такие виды нагружения бруса, при которых в поперечных сечениях возникают одновременно не менее двух внутренних силовых факторов.

Случаи сложного сопротивления условно разделяют на два вида. Первый вид составляют случаи сложного сопротивления, при которых в опасных точках бруса напряженное состояние является одноосным. В эту группу объединяют: изгиб с растяжением, косой изгиб, внецентренное растяжение-сжатие и др.

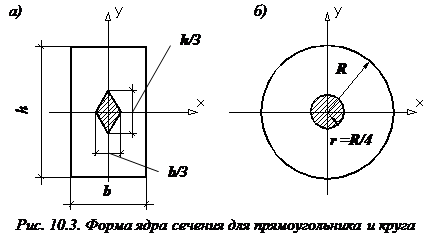
Условие прочности при изгибе с растяжением, пренебрегая действием поперечных сил, имеет вид:

.

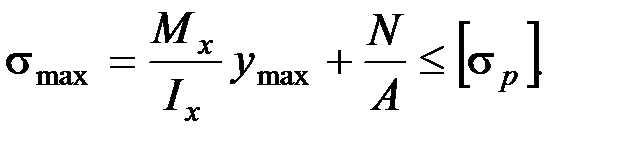Ко второй группе относятся такие случаи сложного сопротивления, когда напряженное состояние является плоским. Например, изгиб с кручением, растяжение(сжатие) с кручением и т.д. Для случая нагружения, относящегося к первой группе, в отличие от второй группы, нет необходимости в применении гипотез прочности.

Косой изгиб проявляется, если прикладываем к балке вертикальную нагрузку, и она при этом изгибается не только в вертикальной плоскости, но и вбок. Косой изгиб - это изгиб, при котором изогнутая ось стержня не лежит в силовой плоскости. Косой изгиб невозможен для балок с сечениями, у которых все центральные оси являются главными (например, квадрат, круг).

Рассмотрим консольную балку прямоугольного сечения длиной l, нагруженную вертикальной силой P. Главная центральная ось балки (ось симметрии) y составляет некоторый малый угол α с направлением действия нагрузки.

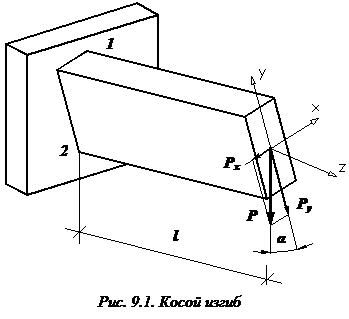
Разложим силу P на составляющие: 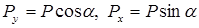. Используя принцип независимости действия сил, рассмотрим отдельно действие каждой составляющей. Нагрузк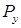и и 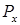вызывают в поперечном сечении, расположенном на некотором расстоянии z от правого конца балки, изгибающие моменты:

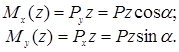
Оба изгибающих момента будут наибольшими в жесткой заделке:

.

Формула суммарных нормальных напряжений при косом изгибе в произвольном поперечном сечении балки для некоторой точки с координатами x и y:

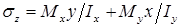, где 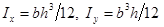– главные моменты инерции; h – высота, а b – ширина прямоугольного поперечного сечения балки. Величины изгибающих моментов и координат данной точки подставляются в формулу нормальных напряжений при косом изгибе, знак каждого из слагаемых определяется по физическому смыслу.

Наибольшие нормальные напряжения при косом изгибе возникнут в поперечном сечении, расположенном в жесткой заделке, в наиболее удаленных от соответствующих нейтральных осейточках 1 и 2:

. В точке 1 напряжения будут растягивающими: 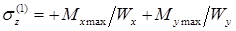, а в точке 2 – такими же по величине, но сжимающими.

В формулах максимальных нормальных напряжений при косом изгибе 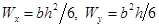– осевые моменты сопротивления балки относительно главных центральных осей инерции.

Нейтральная линия – это геометрическое место точек поперечного сечения стержня, в которых нормальные напряжения равны нулю.

Из определения нейтральной линии легко находится положение нейтральной линии, приравнивая правую часть выражения 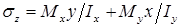к нулю: ,

.

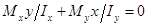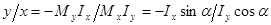При косом изгибе условие прочности имеет вид:

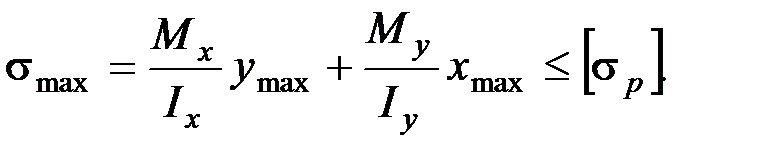
Косой изгиб опасен тем, что при производственном браке (перекосе) могут существенно увеличиться нормальные напряжения в балке.

Внецентренное сжатие.

Внецентренное сжатие. Построениеядра сечения. Изгиб с кручением. Расчеты на прочность при сложном напряженном состоянии.

Внецентренное сжатие – это вид деформации, при котором продольная сила в поперечном сечении стержня приложена не в центре тяжести. При внецентренном сжатии, помимо продольной силы (N), возникают два изгибающих момента ( 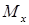и ).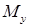

Считают, что стержень обладает большой жесткостью на изгиб, чтобы пренебречь прогибом стержня при внецентренном сжатии.

Преобразуем формулу моментов при внецентренном сжатии , подставляя значения изгибающих моментов: .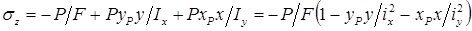

Обозначим координаты некоторой точки нулевой линии при внецентренном сжатии 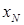, 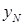и подставим их в формулу нормальных напряжений при внецентренном сжатии. Учитывая, что напряжения в точках нулевой линии равны нулю, после сокращения на 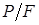, получим уравнение нулевой линии при внецентренном сжатии: .

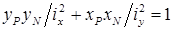Нулевая линия при внецентренном сжатии и точка приложения нагрузки всегда расположены по разные стороны от центра тяжести сечения.

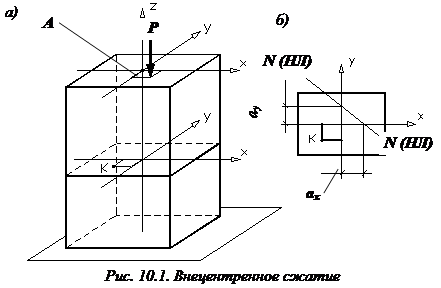
Отрезки, отсекаемые нулевой линией от осей координат, обозначенные и , легко найти из уравнения нулевой линии при внецентренном сжатии. Если сначала принять 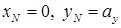, а затем принять 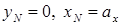, то найдем точки пересечения нулевой линии при внецентренном сжатии с главными центральными осями:

;

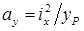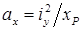
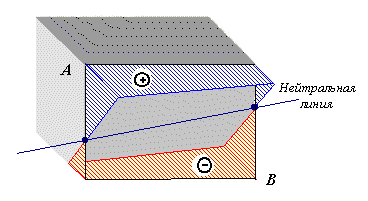
Нулевая линия при внецентренном сжатии разделит поперечное сечение на две части. В одной части напряжения будут сжимающими, в другой – растягивающими. Расчет на прочность, как и в случае косого изгиба, проводят по нормальным напряжениям, возникающим в опасной точке поперечного сечения (наиболее удаленной от нулевой линии).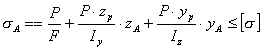

Ядро сечения - малая область вокруг центра тяжести поперечного сечения, характерная тем, что любая сжимающая продольная сила, приложенная внутри ядра, вызывает во всех точках поперечного сечения сжимающие напряжения.

Примеры ядра сечения для прямоугольного и круглого поперечных сечений стержня.

Изгиб с кручением. Такому нагружению (одновременному действию крутящих и изгибающих моментов) часто подвержены валы машин и механизмов. Для расчета бруса необходимо прежде всего установить опасные сечения. Для этого строятся эпюры изгибающих и крутящих моментов.

Рис.1

Используя принцип независимости действия сил, определим напряжения, возникающие в брусе отдельно для кручения, и для изгиба.

При кручении в поперечных сечениях бруса возникают касательные напряжения, достигающие наибольшего значения в точках контура сечения 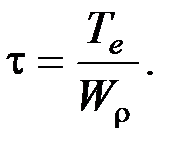При изгибе в поперечных сечениях бруса возникают нормальные напряжения, достигающие наибольшего значения в крайних волокнах бруса .

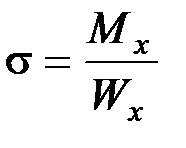Касательные напряжения значительно меньше напряжений от крутящего момента, поэтому ими пренебрегают. Опасное сечение бруса будет у заделки, где действуют максимальные напряжения от изгиба и кручения.

Исследуем напряженное состояние в наиболее опасной точке (рис. 1). Так как напряженное состояние двухосное, то для проверки прочности применяет одну из гипотез.

Применяя третью теорию прочности 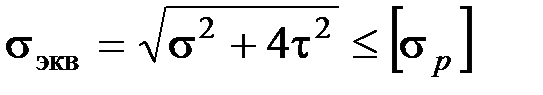и учитывая, что 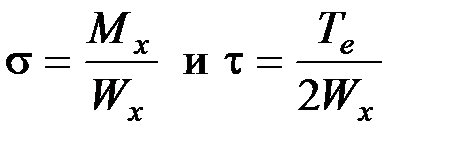, получаем: 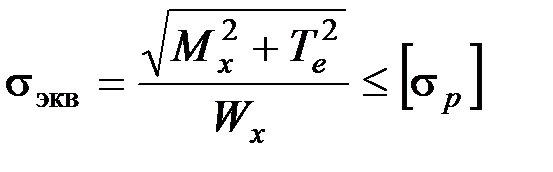. Для подбора сечения находим требуемый момент сопротивления .

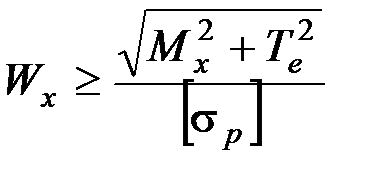Динамические нагрузки.

Виды циклов нагружения.

Усталостная прочность материалов при повторно-переменном нагружении во многом зависит от характера изменения напряжений во времени, от периодической нагрузки.

Периодическая нагрузка – переменная нагрузка с установившимся во времени характером изменения, значения которой повторяются через определенный промежуток (период) времени.

t

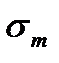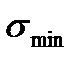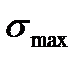Цикл напряжений.

Цикл напряжений – совокупность всех значений переменных напряжений за время одного периода изменения нагрузки.

Обычно цикл напряжений характеризуется двумя основными параметрами цикла:

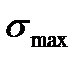- максимальное напряжение цикла; 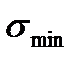- минимальное напряжение

цикла;

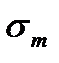- среднее напряжение цикла: ;

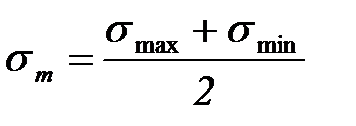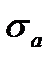- амплитудное напряжение цикла: ;

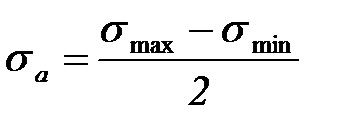R – коэффициент асимметрии цикла напряжении:

t

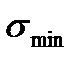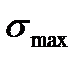Симметричный цикл.

.

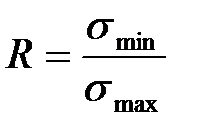В зависимости от величины перечисленных характеристик циклы напряжений могут быть подразделены на следующие основные типы:

Симметричный цикл – максимальное и минимальное напряжения равны по абсолютной величине и противоположны по знаку 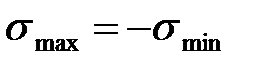, R= –1;

t

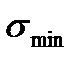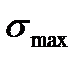Асимметричный цикл.

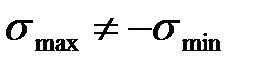Асимметричный цикл - максимальное и минимальное напряжения не равны по абсолютной величине ( ), при этом асимметричный цикл может быть знакопеременным или знакопостоянным;

Знакопеременный цикл - максимальное и минимальное напряжения не равны по абсолютной величине и противоположны по знаку ( , , );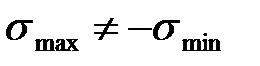

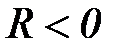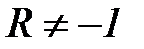Знакопостоянный цикл - максимальное и минимальное напряжения не равны по абсолютной величине и имеют одинаковый знак ( , , );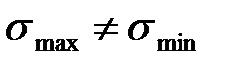

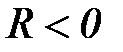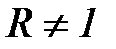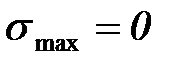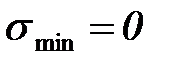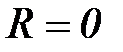Отнулевой (пульсирующий) цикл – максимальное или минимальное напряжения равны нулю ( или , или ).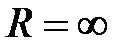

Кривая усталости (кривая Веллера)

Кривая усталости (рис.1) строится на основании результатов усталостных испытаний при симметричном цикле.

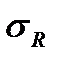N

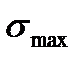Рис.1 Кривая Веллера.

Кривая усталости показывает, что с увеличением числа цикла максимальное напряжение, при котором происходит разрушение материала, значительно уменьша-ется. При этом для многих материалов, например углеродис-той стали, можно установить такое наибольшее напряжение цикла, при котором образец не разрушается после любого числа циклов (горизонтальный участок диаграммы), называемое пределом выносливости ( ).

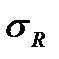Предел выносливости (усталости) 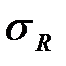- наибольшее (предельное) напряжение цикла, при котором не происходит усталостного разрушения образца после произвольно большого числа циклов.

Так как испытания нельзя проводить бесконечно большое время, то число циклов ограничивают некоторым пределом, который называют базовым числом циклов. В этом случае, если образец выдерживает базовое число циклов (для черных металлов – N = 10⁷), то считается, что напряжение в нем не выше предела выносливости.

Ударные нагрузки.

Основы расчетов на ударное нагружение. Динамический коэффициент. Случаи удара при простейших деформациях.

Явление удара получается в том случае, когда скорость рассматриваемой части конструкции или соприкасающихся с ней частей изменяется в очень короткий период времени.

Таким образом, в ударяемой части конструкции возникают такие напряжения, как будто к ней была приложена сила инерции ударяющего тела; мы можем вычислить эти напряжения, рассматривая силу инерции 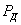как статическую нагрузку нашей конструкции. Затруднение заключается в вычислении этой силы инерции. Продолжительности удара, т. е. величины того промежутка времени, в течении которого происходит падение скорости до нуля, мы не знаем. Поэтому остается неизвестной величина ускорения, а стало быть, и силы 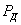. Таким образом, хотя вычисление напряжений при ударе представляет собой частный случай задачи учета сил инерции, однако для вычисления силы 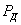и связанных с ней напряжений и деформаций здесь приходится применять иной прием и пользоваться законом сохранения энергии.

Применяя закон сохранения энергии, надо:

1) вычислить кинетическую энергию ударяющего тела Т;

2) вычислить потенциальную энергию 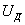тел, воспринимающих удар, под нагрузкой их силами инерции при ударе; потенциальная энергия должна быть выражена через напряжение ( 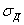, 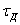) в каком-либо сечении, через деформацию (удлинение, прогиб) или через силу инерции 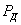ударяющего тела;

3) приравнять величины 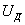и Т и из полученного уравнения найти или непосредственно динамическое напряжение, или деформацию, а по ней, пользуясь законом Гука, напряжение или силу 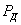и соответствующие ей динамические напряжения и деформации.

При ударе происходит очень быстрое превращение одного вида энергии в другой: кинетическая энергия ударяющего тела превращается в потенциальную энергию деформации. Выражая эту энергию в функции силы 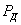или напряжений, или деформаций получаем возможность вычислить эти величины.

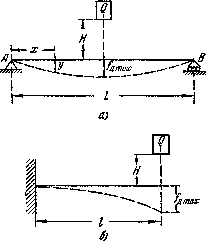
Рис.2 Модель поперечного удара.

Полагая, что кинетическая энергия Т ударяющего тела полностью переходит в потенциальную энергию 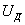деформации упругой системы, можем написать:.

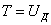(1)

Так как к моменту окончания деформации ударяющее тело пройдет путь 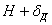, то его запас энергии будет измеряться произведенной им работой 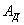и будет равен:

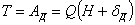
Вид формулы для 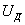при ударе примем тот же, что и при статическом нагружении системы С силой инерции 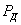, т. е.

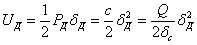
Подставляя значения Т и 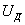в уравнение (1), получаем:

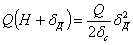или

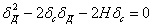
Отсюда

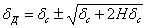, или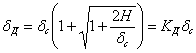

Обозначив 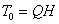—энергия ударяющего тела к моменту начала удара, выражение для динамического коэффициента может быть представлено еще и в таком виде:

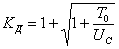
Формулы 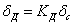и 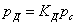, в которых 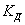выражается через 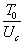, могут быть использованы также для решения задачи о встречном ударе тел, двигающихся с некоторой скоростью.

Описанный общий прием расчета на удар предполагает, что вся кинетическая энергия ударяющего тела целиком переходит в потенциальную энергию деформации упругой системы. Это предположение не точно. Кинетическая энергия падающего груза частично превращается в тепловую энергию и энергию неупругой деформации основания, на которое опирается система.

Вместе с тем при высоких скоростях удара деформация за время удара не успевает распространиться на весь объем ударяемого тела и в месте удара возникают значительные местные напряжения, иногда превосходящие предел текучести материала.

Рассмотрим некоторые случаи удара при простейших деформациях. При этом для нахождения коэффициента динамичности применим основные полученные формулы для динамического коэффициента.

Для определения 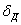, 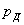и 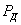используем зависимости:

и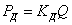

При изгибе величина статической деформации 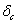, представляющей собой статический прогиб балки 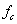с в мес