Критерий пессимизма-оптимизма Гурвица

При выборе решения он рекомендует руководствоваться некоторым средним результатом, характеризующим состояние между крайним пессимизмом и безудержным оптимизмом, т.е. критерий выбирает альтернативу с максимальным средним результатом (при этом действует негласное предположение, что каждое из возможных состояний среды может наступить с равной вероятностью). Формально данный критерий выглядит так:

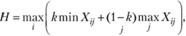(2.12)

где k – коэффициент пессимизма, который принадлежит промежутку от 0 до 1 в зависимости от того, как принимающий решение оценивает ситуацию. Если он подходит к ней оптимистически, то эта величина должна быть больше 0,5. При пессимистической оценке он должен взять упомянутую величину меньше 0,5.

При k = 0 критерий Гурвица совпадает с максимаксным критерием, а при k = 1 – с критерием Вальда.

Рассчитаем критерий Гурвица для условий нашего примера, придав упомянутому параметру значение на уровне 0,6:

H, = 16 × 0,6 + (-6) × 0,4 = 7,2;

Н2= 12×0,6 + 2×0,4 =8;

Н3 = 6 × 0,6 + 0 × 0,4 = 3,6.

По максимуму значения данного критерия надо принять решение о переходе к массовому выпуску новой продукции через год.

В пашем примере стратегия А2 фигурирует в качестве оптимальной по трем критериям выбора из четырех испытанных, степень ее надежности можно признать достаточно высокой для того, чтобы рекомендовать эту стратегию к практическому применению. Действительно, при таком решении не придется особенно сожалеть об упущенной прибыли и не придется ожидать больших убытков, т.е. сразу минимизируются и сожаления об упущенной прибыли, и возможные убытки.

Имитационное моделирование по методу Монте-Карло (Monte-Carlo Simulation). Оно позволяет построить математическую модель для проекта с неопределенными значениями параметров и, зная вероятностные распределения параметров проекта, а также связь между изменениями параметров (корреляцию), получить распределение доходности проекта.

Процедура имитации Монте-Карло базируется на последовательности следующих шагов (рис. 2.12).

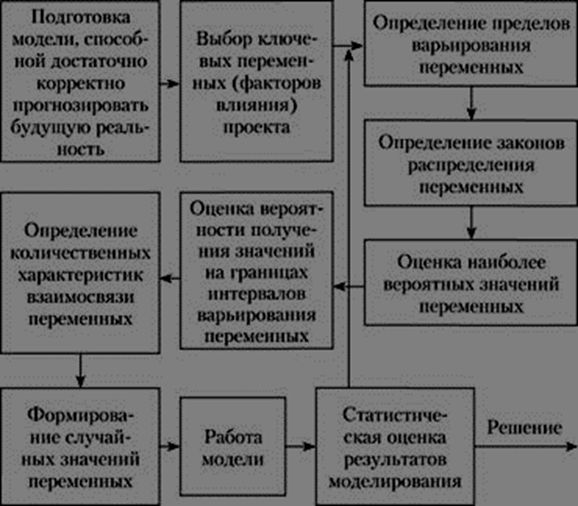
Рис. 2.12. Последовательность анализа рисков инвестиционного проекта с использованием метода Монте-Карло

Метод Монте-Карло наиболее полно характеризует весь спектр неопределенностей, с которой может столкнуться реальный инвестиционный проект, и через задаваемые изначально ограничения позволяет учитывать всю доступную проектному аналитику информацию. Практическая реализация метода возможна только с применением компьютерных программ, позволяющих описывать прогнозные модели и рассчитывать большое число случайных сценариев.

Одним из программных продуктов, реализующих метод Монте-Карло, является пакет Risk Master (RM), разработанный в Гарвардском университете с целью обучения студентов экспертизе инвестиционных проектов.

Структурно программа RM включает два блока – имитационный и аналитический. В ходе работы первого из них происходит имитация методом Монте-Карло модели инвестиционного проекта, построенной в электронных таблицах. Задачей второго блока программы является анализ полученных на первом этапе результатов и вычисление показателей совокупного риска проекта.

В процессе работы программы RM математическая модель проекта подвергается повторяющимся имитациям, в ходе каждой из которых ключевые рисковые переменные выбираются случайным образом в соответствии с заранее заданными распределениями вероятностей и условиями корреляции. Затем проводится статистический анализ результатов всех имитаций для получения распределения вероятностей результирующего показателя проекта.

Рассмотрим эти стадии подробнее.

1. Построение математической модели инвестиционного проекта – это первая стадия анализа рисков в соответствии с программой RM. Модель содержит алгебраические и (или) логические соотношения между его факторами (переменными). Она должна включать в себя все важные для проекта переменные (и не включать лишних), а также правильно отражать корреляционные связи между ними. Кроме того, одно из важных требований при разработке модели состоит в необходимости точно предсказывать проектный результат, получаемый на основании внутримодельной обработки входной информации.

Успешное завершение первого этапа позволяет перейти к следующему. Среди известных и важных для проекта факторов выявляются ключевые рисковые проектные переменные. Риск проекта в целом представляет собой функцию риска отдельных переменных оценочной модели, поэтому следует различать, во-первых, те из них, к которым очень чувствителен результат проекта, и, во-вторых, те, которые обладают высокой степенью неопределенности (сильный разброс значений). Другими словами, есть переменные, значения которых варьируют в большом интервале, не оказывая существенного влияния на отдачу проекта, и есть переменные достаточно стабильные, но даже небольшие отклонения их значений могут вызывать значительный разброс отдачи проекта. Поэтому разбиение всех факторов проекта на соответствующие группы является необходимым по двум причинам: во-первых, чем больше рисковых переменных включено в математическую модель, тем сложнее отразить все корреляционные связи между ними; во-вторых, затраты, необходимые для нахождения распределений вероятностей и корреляционных зависимостей большого числа переменных, могут превысить выгоду от включения этих переменных в модель.

В связи с этим представляется целесообразным сфокусировать внимание и имеющиеся ресурсы па определении и проверке предположений относительно наиболее чувствительных (анализ чувствительности) и неопределенных (анализ неопределенности) факторов модели.

Затем в два этапа осуществляется определение распределений вероятностей для выбранных ключевых рисковых переменных.

Первый этап – определение возможного разброса значений для каждой переменной, заключающееся в установлении максимального и минимального значений переменной, т.е. границ, в которых предположительно будут колебаться ее значения.

Второй этап – определение распределений вероятностей. По прошлым наблюдениям за переменной можно установить частоту, с которой та принимает соответствующие значения. В этом случае вероятностное распределение есть то же самое частотное распределение, показывающее частоту встречаемости значения, правда, в относительном масштабе (от 0 до 1). Вероятностное распределение регулирует вероятность выбора значений из определенного интервала. В соответствии с заданным распределением модель оценки рисков будет выбирать произвольные значения переменной. До рассмотрения рисков мы подразумевали, что переменная принимает одно определенное нами значение с вероятностью, равной 1. И через единственную итерацию расчетов мы получали однозначно определенный результат. В рамках модели вероятностного анализа рисков проводится большое число итераций, позволяющих установить, как ведет себя результативный показатель (в каких пределах колеблется, как распределен) при подстановке в модель различных значений переменной в соответствии с заданным распределением.

Задача аналитика, занимающегося анализом риска, состоит в том, чтобы хотя бы приблизительно определить для исследуемой переменной вид вероятностного распределения. При этом основные вероятностные распределения, используемые в анализе рисков, могут быть симметричными (например, нормальное, равномерное, треугольное) и несимметричными (например, пошаговое) (рис. 2.13).

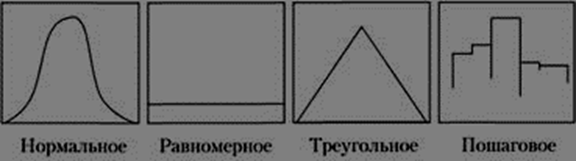
Рис. 2.13. Виды распределений вероятностей, используемых в программе Risk Master

Этап установления корреляционных связей является очень важным для результативности всего процесса анализа рисков, так как ошибки в выявлении существующих коррелированных переменных модели ведут к серьезным искажениям модельных результатов. Допустим, что цена и количество проданного продукта есть две отрицательно коррелированные переменные. Если не будет учтена связь между ними (коэффициент корреляции), то возможны сценарии, случайно вырабатываемые компьютером, где цена и количество проданной продукции будут либо высоки, либо низки, что негативно отразится на результатах. Поэтому перед проведением имитационных расчетов необходимо выявить все корреляционные зависимости и задать значения коэффициентов корреляции. К достоинствам программного пакета RM относится возможность отражения множественных корреляционных связей.

2. Стадия анализа рисков – проведение расчетных итераций – почти полностью выполняется компьютером, на долю аналитика проектных рисков выпадает лишь необходимость задать количество проводимых итераций (от 8 до 10 000). 200–500 итераций обычно достаточно для получения хорошей репрезентативной выборки. В процессе каждой итерации происходит случайный выбор значений ключевых переменных специфицированного интервала в соответствии с вероятностными распределениями и условиями корреляции. Затем рассчитываются и сохраняются результативные показатели (например, NPV). И так далее, от итерации к итерации.

3. Анализ результатов, интерпретация результатов, полученных в ходе итерационных расчетов, – последняя стадия в анализе проектных рисков.

Результаты анализа рисков можно представить в виде профиля риска (рис. 2.14). На нем графически показывается вероятность каждого возможного случая (имеются в виду вероятности возможных значений результативного показателя). Часто при сравнении вариантов капиталовложений удобнее пользоваться кривой, построенной на основе суммы вероятностей (кумулятивный профиль риска). Такая кривая показывает вероятность того, что результативный показатель проекта будет больше или меньше определенного значения. Проектный риск, таким образом, описывается положением и наклоном кумулятивного профиля риска.

Рис. 2.14. График функции распределения вероятности результативною показателя

Рассмотрим пять иллюстративных случаев принятия решений. Случаи 1–3 связаны с решением инвестировать в отдельно взятый проект, тогда как два последних случая (4, 5) относятся к решению-выбору из альтернативных проектов. В каждом случае рассматривается как кумулятивный, так и некумулятивный профили риска для сравнительных целей. Кумулятивный профиль риска более полезен в случае выбора наилучшего проекта из представленных альтернатив, в то время как некумулятивный профиль риска лучше индуцирует вид распределения и показателен для понимания концепций, связанных с определением математического ожидания. Анализ базируется на показателе чистой текущей стоимости NPV.

Случай 1. Минимально возможное значение NPV выше, чем нулевое (рис. 2.15, кривая 1). Вероятность отрицательного NPV равна 0, так как нижний конец кумулятивного профиля риска лежит справа от нулевого значения NPV. Поскольку данный проект имеет положительное значение NPV во всех случаях, ясно, что проект принимается.

Случай 2. Максимально возможное значение NPV ниже нулевого (рис. 2.15, кривая 2). Вероятность положительного NPV равна 0 (см. следующий рисунок), так как верхний конец кумулятивного профиля риска лежит слева от нулевого значения NPV. Поскольку данный проект имеет отрицательное значение NPV во всех случаях, ясно, что проект не принимается.

Случай 3. Максимальное значение NPV больше, а минимальное меньше нулевого (рис. 2.15, кривая 3). Вероятность нулевого NPV больше, чем 0, но меньше, чем 1, так как вертикаль нулевого NPV пересекает кумулятивный профиль рисков. Поскольку NPV может быть как отрицательным, так и положительным, решение будет зависеть от предрасположенности к риску инвестора. По-видимому, если математическое ожидание NPV меньше или равно 0 (пик профиля рисков слева от вертикали или вертикаль точно проходит по пику), проект должен быть отклонен от дальнейшего рассмотрения.

Случай 4. Непересекающиеся кумулятивные профили рисков альтернативных (взаимоисключающих) проектов (рис. 2.16). При фиксированной вероятности отдача проекта В всегда выше, чем у проекта А. Профиль рисков также говорит о том, что при фиксированной NPV вероятность, с которой та будет достигнута, начиная с некоторого уровня будет выше для проекта В, чем для проекта А. Таким образом, мы подошли к правилу 1.

Правило 1. Если кумулятивные профили рисков двух альтернативных проектов не пересекаются ни в одной точке, тогда следует выбирать тот проект, чей профиль рисков расположен правее.

Случай 5. Пересекающиеся кумулятивные профили рисков альтернативных проектов (рис. 2.17). Склонные к риску инвесторы предпочтут возможность получения высокой прибыли и выберут проект А. Несклонные к риску инвесторы предпочтут возможность нести низкие потери и, вероятно, выберут проект В.

Правило 2. Если кумулятивные профили риска альтернативных проектов пересекаются в какой-либо точке, то решение об инвестировании зависит от склонности к риску инвестора.

Рис. 2.15. Графическая иллюстрация случаев 1–3

Рис. 2.16. Графическая иллюстрация случая 4

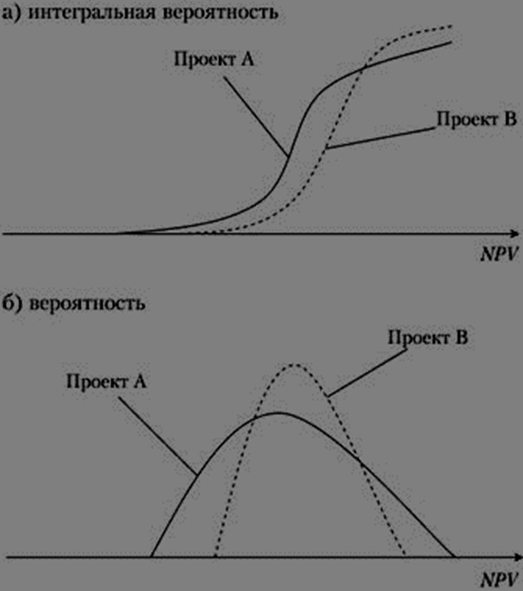
Рис. 2.17. Графическая иллюстрация случая 5

Рассмотрим наиболее распространенные показатели совокупного риска проекта.

Ожидаемая стоимость агрегирует информацию, содержащуюся в вероятностном распределении. Она получается умножением каждого значения результативного показателя на соответствующую вероятность и последующего суммирования результатов. Сумма всех отрицательных значений показателя, перемноженных на соответствующие вероятности, есть ожидаемый убыток. Ожидаемый выигрыш – сумма всех положительных значений показателя, перемноженных на соответствующие вероятности. Ожидаемая стоимость есть, конечно, их сумма.

В качестве индикатора риска ожидаемая стоимость может выступать как надежная оценка только в ситуациях, где операция, связанная с данным риском, может быть повторена много раз. Хорошим примером такого риска служит риск, страхуемый страховыми компаниями, когда последние предлагают обычно одинаковые контракты большому числу клиентов. В инвестиционном проектировании мера ожидаемой стоимости должна всегда применяться в комбинации с мерой вариации, такой как стандартное отклонение.

Инвестиционное решение не должно базироваться лишь на одном значении ожидаемой стоимости, потому что индивид не может быть равнодушен к различным комбинациям значения показателя отдачи и соответствующей вероятности, из которых складывается ожидаемая стоимость.

Издержки неопределенности, или ценность информации, как они иногда называются, – полезное понятие, помогающее определить максимально возможную плату за получение информации, сокращающей неопределенность проекта. Эти издержки можно определить как ожидаемую стоимость возможного выигрыша при решении отклонить проект или как ожидаемую стоимость возможного убытка при решении принять проект.

Ожидаемая стоимость возможного выигрыша при решении отклонить проект равна сумме возможных положительных значений NPV, перемноженных на соответствующие вероятности (рис. 2.18).

Рис. 2.18. Ожидаемая стоимость возможного выигрыша при решении отложить проект

Ожидаемая стоимость возможного убытка при решении принять проект, показанная в виде заштрихованной площади на рис. 2.19, равна сумме возможных отрицательных значений NPV, перемноженных на соответствующие вероятности.

Рис. 2.19. Ожидаемая стоимость возможного убытка при решении принять проект

Оценив возможное сокращение издержек неопределенности при приобретении дополнительной информации, инвестор решает, отложить решение принять или отклонить проект и искать дополнительную информацию или принимать решение немедленно. Общее правило таково: инвестору следует отложить решение, если возможное сокращение в издержках неопределенности превосходит издержки добывания дополнительной информации.

Нормированный ожидаемый убыток – отношение ожидаемого убытка к ожидаемой стоимости. Этот показатель может принимать значения от 0 (отсутствие ожидаемого убытка) до 1 (отсутствие ожидаемого выигрыша).

На рис. 2.19 он представляется как отношение площади под профилем риска слева от нулевого NPV ко всей площади под профилем риска.

Проект с вероятностным распределением NPV, таким, что область определения профиля риска NPV выше 0, имеет нормируемый ожидаемый убыток, равный 0, что означает абсолютную неподверженность риску проекта. Проект, область определения профиля риска NPV которого ниже 0, полностью подвержен риску.

Данный показатель определяет риск как следствие двух вещей: наклона и положения профиля риска NPV по отношению к разделяющей вертикали нулевого NPV.

Метод Монте-Карло, несмотря на свои достоинства, не распространен и не используется слишком широко в бизнесе. Одна из главных причин этого – неопределенность функций плотности переменных, которые применяются при подсчете потоков наличности.

Другая проблема, которая возникает как при использовании метода сценариев, так и при использовании метода Монте-Карло, состоит в том, что оба метода не дают однозначного ответа на вопрос, следует ли реализовывать данный проект или отвергнуть его.

При завершении анализа, проведенного методом Монте- Карло, у эксперта есть значение ожидаемой чистой текущей стоимости проекта и плотность распределения этой случайной величины. Однако наличие этих данных не обеспечивает аналитика информацией о том, действительно ли прибыльность проекта достаточно велика, чтобы компенсировать риск по проекту, оцененный стандартным отклонением и коэффициентом вариации.

Ряд исследователей избегают использования данного метода ввиду сложности построения вероятностной модели и множества вычислений, однако при корректности модели метод дает весьма надежные результаты, позволяющие судить как о доходности проекта, так и о его устойчивости (чувствительности).

В зависимости от результатов завершенного анализа рисков, а также от того, насколько склонен к риску инвестор, последний принимает решение принять, изменить или отклонить проект.

Например, инвестор, исходя из своей склонности к риску, действовал бы следующим образом.

• Риск ≥ 30%. В случае если показатель риска, а это прежде всего нормированный ожидаемый убыток (НОУ), равен или превышает 30%, то для принятия проекта необходимо предварительно внести и осуществить предложения по снижению риска. Под предложениями понимаются любые действия по изменению данных на входе, способные уменьшить риск, не обрекая проект на убыточность.

В этих целях используются разработанные заранее правила поведения участников в определенных "нештатных" ситуациях (например, сценарии, предусматривающие соответствующие действия участников при тех или иных изменениях условий реализации проекта).

В проектах могут предусматриваться также специфические механизмы стабилизации, обеспечивающие защиту интересов участников при неблагоприятном изменении условий реализации проекта (в том числе в случаях, когда цели проекта будут достигнуты не полностью или не достигнуты вообще) и предотвращающие возможные действия участников, ставящие под угрозу его успешную реализацию. В одном случае может быть снижена степень самого риска (за счет дополнительных затрат на создание резервов и запасов, совершенствование технологий, уменьшение аварийности производства, материальное стимулирование повышения качества продукции), в другом – риск перераспределяется между участниками (индексирование цен, предоставление гарантий, различные формы страхования, залог имущества, система взаимных санкций).

Как правило, применение в проекте стабилизационных механизмов требует от участников дополнительных затрат, размер которых зависит от условий реализации мероприятия, ожиданий и интересов участников, их оценок степени возможного риска. Такие затраты подлежат обязательному учету при определении эффективности проекта.

Здесь работает балансировка между риском и прибыльностью. Если на этом этапе удается снизить риск так, что нормированный ожидаемый убыток становится меньше 30%, и есть выбор среди такого рода вариантов проекта, то лучше выбрать тот из них, у которого коэффициент вариации меньше. Если же не удается снизить риск до указанной отметки, проект отклоняется.

• Риск < 30%. Проекты с риском менее 30% (нормированный ожидаемый убыток меньше 30%) лучше подстраховать. Предлагается создать страховой фонд в размере определенной доли от основной суммы инвестирования. Как определить эту долю – это вопрос методики. Можно принять ее равной значению показателя риска нормированного ожидаемого убытка. Например, если вероятность риска равна 0,25, то необходимо предусмотреть отчисления от нераспределенной прибыли в процессе осуществления проекта или заключить договор со страховой компанией на сумму в размере 25% от основной суммы инвестирования и направить эти деньги в резерв, подлежащий использованию только в случае наступления крайних ситуаций, связанных, скажем, с незапланированным недостатком свободных денежных средств, а также другими проблемами, в целях нормализации финансово-экономической ситуации. На самом деле источник оплаты страхового фонда скорее всего будет зависеть от периода осуществления проекта. В самый трудный в финансовом отношении начальный момент осуществления проекта у предприятия вряд ли найдется возможность обойтись без внешнего окружения при создании страхового фонда, например на базе страховой компании. Но по мере осуществления проекта у предприятия накапливается прибыль, ежегодные отчисления от которой могли бы составить страховой фонд.

18. Пример линейной регрессии. Другие виды регрессионных моделей.

Линия регрессии

Математическое уравнение, которое оценивает линию простой (парной) линейной регрессии:

Y=a+bx.

x называется независимой переменной или предиктором.

Y – зависимая переменная или переменная отклика. Это значение, которое мы ожидаем для y (в среднем), если мы знаем величину x, т.е. это «предсказанное значение y»

· a – свободный член (пересечение) линии оценки; это значение Y, когда x=0 (Рис.1).

· b – угловой коэффициент или градиент оценённой линии; она представляет собой величину, на которую Y увеличивается в среднем, если мы увеличиваем x на одну единицу.

· a и b называют коэффициентами регрессии оценённой линии, хотя этот термин часто используют только для b.

Парную линейную регрессию можно расширить, включив в нее более одной независимой переменной; в этом случае она известна как множественная регрессия.

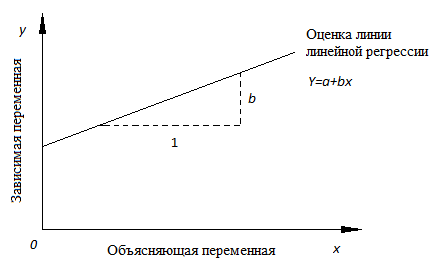
Рис.1. Линия линейной регрессии, показывающая пересечение a и угловой коэффициент b (величину возрастания Y при увеличении x на одну единицу)

Вычисляемая с помощью метода наименьших квадратовпрямая линия называется линией регрессии. Она характеризуется тем, что сумма квадратов расстояний от точек на диаграмме до этой линии минимальна (по сравнению со всеми возможными линиями).

Линия регрессии дает наилучшее приближенное описание линейной зависимости между двумя переменными. http://iskunstvo.info/materials/history/2/inf/regr.htm

Виды регрессионных моделей

1. Простая линейная регрессия - самый простой случай - установление линейной связи между одной независимой (одномерной) переменной х и одной зависимой переменной (откликом) у.

2. Множественная линейная регрессия - задача предполагает установление линейной зависимости между группой независимых переменных Х₁,Х₂, … Х_К и одномерным откликом у. Стратегия анализа адекватности подобранной модели в задаче мно­жественной регрессии в целом аналогична задаче простой регрессии и сводится к детальному анализу остатков.

При решении задач множественной регрес­сии самым главным является выбор тех переменных, которые оказывают существенное влияние на отклик, и отсеивание несущественных переменных. Для этого используют очень эффективные на практике методы шаговой регрессии.

В подобных задачах может являться эффект, когда каждая из переменных не только действует на отклик независимо от других, но и порождает совместное воздействие. Для учёта этого совместного воздействия в модель, кроме переменных можно включать их произведения, например переменные Х₁ • Х₂, X₁ • Х₃ и т.д.

3. Нелинейная регрессия.В этом случае параметры модели входят в подбираемую регрессионную функцию нелинейным образом. Нахождение их оценок в этом случае представляет собой более сложную задачу.

4. Множественная нелинейная регрессия- ещё более сложная задача, так как в данном случае нелинейность может сочетаться с взаимодействием факторов. Существует мнение, что использование методов нелинейной регрессии, особенно множественной нелинейной регрессии, оправдано лишь в том случае, когда вид регрессионной зависимости известен априори. Однако опыт показывает, что при наличии современных быстродействующих программных средств и известной осторожности в применении (постоянное использование t-критерия и сравнения достоверности разных моделей) такая регрессия может оказаться очень эффективной. Она в ряде случаев позволяет обнаружить новые закономерности, которые лишь впоследствии находят теоретическое объяснение.

Возможности современных машинных методов в построении регрессионных моделей. Объём оперативной памяти современных компьютеров при использовании специальных программных средств позволяет решать все перечисленные задачи без исключения. Вопрос обычно стоит о возможностях офисной техники без привлечения специальных программ. В этом отношении задачи первого и второго типа свободно решаются в рамках инструмента анализа «Регрессия». Задачу третьего типа можно решать в рамках графических опций MS EXCEL (глава 5). И лишь решение задачи четвёртого типа требует использования специальных программных средств, из которых наиболее востребованной считается русскоязычная версия программы STATISTICA.

19. Типы нелинейных регрессионных моделей. МНК – метод оценки коэффициентов. Пример.

Основные типы нелинейных моделей

1. Регрессионные модели с линейной структурой

2. Существенно нелинейные регрессионные модели. (дальше подробнее о каждой)