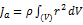Вопрос 12 Геометрические и физические приложения опр. инт-ла

1.1 Вычисление площади плоской фигуры

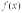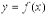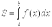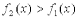Пусть функция непрерывна и неотрицательна на отрезке [a, b]. Тогда площадь фигуры, ограниченной осью ОХ, отрезками прямых x = a, x = b и графиком функции , может быть вычислена по формуле Если на отрезке [a, b], 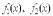- непрерывные функции, то площадь фигуры, ограниченной прямыми х = а, x = b, графиками функций 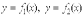вычисляется по формуле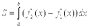

1.2. Вычисление площади криволинейного сектора.

Пусть кривая AB задана в полярных координатах уравнением 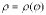, , 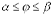причем 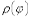- непрерывная и неотрицательная на отрезке 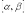функция. Фигуру, ограниченную кривой AB и двумя полярными радиусами, составляющими с полярной осью углы 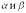, будем называть криволинейным сектором.

Площадь криволинейного сектора может быть вычислена по формуле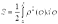

1.3 Вычисление площади плоской фигуры, если граница задана параметрически

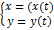Кривая замкнута α<t<β . Граница обходится в положит. напр при t от α до β => область остается слева.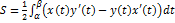

2. Вычисление длины дуги плоской кривой

2.1 Если функция y = f(x) непрерывна вместе с её производной f'(x) на отрезке [a, b], то длина дуги AB, где A(a,f(a)), B(b, f(b)), выражается формулой .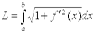

2.2. Если кривая задана параметрическими уравнениями 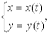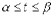, где x(t), y(t) - дифференцируемые функции, то длина дуги .

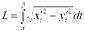2.3. Если дуга задана в полярных координатах 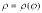, , 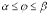то длина дуги

.

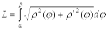3. Вычисление объемов.

3.1. Вычисление объема тела по известным площадям параллельных сечений.

Если известны площади сечений тела плоскостями, перпендикулярными оси OX, т. е., зная х, мы можем вычислить площадь сечения S = S (x). Тогда объем тела 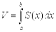в предположении, что S(x) - интегрируемая функция.

3.2. Вычисление объема тела вращения:

а) Кривая трапеция до Ох вращается вокруг Ох: если тело образовано вращением криволинейной трапеции, ограниченной кривой y = f(x), осью OX и двумя прямыми x = a и x = b(a < b) вокруг оси OX, то объем тела ;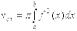

б) Кривая трапеция до Оу вращается вокруг Оу: если тело образовано вращением фигуры, ограниченной кривой 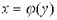, прямыми y=c, y=d (c<d) и осью OY, вокруг оси OY, то его объем ;

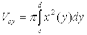в) Трапеция до Ох вращается вокруг Оу: если тело образовано вращением вокруг оси OY фигуры, ограниченной линией y = f (x), прямыми x = a, x = b 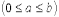и осью OX, то его объем можно вычислить по формуле ;

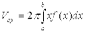г) если вращается вокруг полярной оси криволинейный сектор, ограниченный дугой 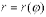, двумя полярными радиусам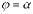и и 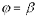, то объем полученного тела может быть вычислен по формуле .

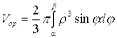4. Вычисление площади поверхности вращения

4.1. Поверхность, обр вращением кривой 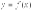, a < x < b вокруг оси OX, имеет площадь .

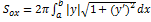4.2. Если кривая задана параметрическими уравнениями 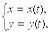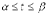, причем 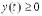, то .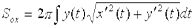

4.3. Если дуга 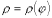, , 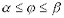задана в полярной системе координат кривой, и вращается вокруг полярной оси, то площадь поверхности вращения можно вычислить по формуле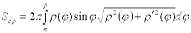

5.Вычисление статических моментов

Пусть на плоскости Оху задана система материальных точек M₁ (x₁; y₁), М₂(х₂; у₂),..., Мn(хn; уn) соответственно с массами m₁, m₂,... ...,m_n.

Статическим моментом S_x системы материальных точек относительно оси Ох называется сумма произведений масс этих точек на их ординаты (т. е. на расстояния этих точек от оси Ох):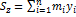

Аналогично определяется статический момент Sy этой системы относительно оси Oy: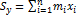

Если массы распределены непрерывным образом вдоль некоторой кривой, то для выражения статического момента понадобится интегрирование.

6. Вычисление моментов инерции

Осевой момент инерции тела J_a является мерой инертности тела во вращательном движении вокруг оси подобно тому, как масса тела является мерой его инертности в поступательном движении: 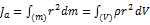где:

dm = ρ dV — масса малого элемента объёма тела dV,

ρ — плотность,

r — расстояние от элемента dV до оси a.

Если тело однородно, то есть его плотность всюду одинакова, то