Гармоническая функция времени и ее параметры»
Гармонической функциейвремени называются функция, изменяющаяся по косинусоидальному или синусоидальному закону. В радиотехнической литературе традиционно используют косинусоидальную форму записи гармонической функции времени
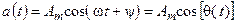 , (4.4)
, (4.4)
где 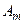 ,
, 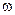 и
и 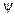 — амплитуда, угловая частота и начальная фаза гармонической функции соответственно;
— амплитуда, угловая частота и начальная фаза гармонической функции соответственно; 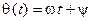 — мгновенная фаза гармонической функции.
— мгновенная фаза гармонической функции.
Угловая частота является скоростью изменения мгновенной фазы
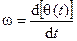 .
.
В Международной системе единиц СИ мгновенная фаза и начальная фаз — в радианах или градусах, а угловая частота измеряется в радианах в секунду (рад/с).
Периодом периодической функции времени называется наименьший промежуток времени 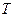 , через который значения функции повторяются, то есть
, через который значения функции повторяются, то есть 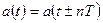 , где
, где 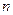 — целое число. В Международной системе единиц СИ период измеряется в секундах.
— целое число. В Международной системе единиц СИ период измеряется в секундах.
Частотой 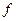 периодической функции времени называется величина, обратная периоду:
периодической функции времени называется величина, обратная периоду: 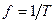 . В Международной системе единиц СИ частота измеряется в герцах (Гц).
. В Международной системе единиц СИ частота измеряется в герцах (Гц).
Угловая частота 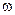 , период
, период 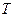 и частота
и частота 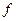 связаны соотношением
связаны соотношением
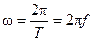 .
.
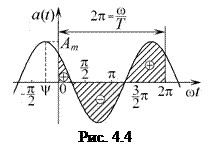 При построении временных диаграмм (рис. 4.4) гармонических функций по оси абсцисс обычно откладывают не время
При построении временных диаграмм (рис. 4.4) гармонических функций по оси абсцисс обычно откладывают не время  , а величин
, а величин 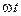 , пропорциональную времени и имеющую размерность фазы, измеряемой в градусах или радианах. Поскольку начальная фаза
, пропорциональную времени и имеющую размерность фазы, измеряемой в градусах или радианах. Поскольку начальная фаза 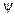 гармонической функции (4.4) представляет собой значение мгновенной фазы
гармонической функции (4.4) представляет собой значение мгновенной фазы 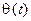 в момент
в момент 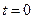 , то есть
, то есть 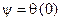 , то на временной диаграмме (рис. 4.4) начальная фаза
, то на временной диаграмме (рис. 4.4) начальная фаза 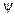 равна смещение максимума этой функции относительно начала координат
равна смещение максимума этой функции относительно начала координат 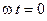 . Если этот максимум смещён влево относительно начала координат, то начальная фаза положительна
. Если этот максимум смещён влево относительно начала координат, то начальная фаза положительна 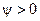 , а если — вправо, то отрицательна
, а если — вправо, то отрицательна 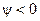 .
.
Положительным (отрицательным) полупериодом (полуволной) гармонической функции называется интервал времени, в течение которого значения этой функции положительны (отрицательны) (см. рис. 4.4).
На рис. 4.5 изображены временные диаграммы двух гармонических функций:
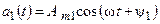 ;
;
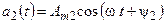 ,
,
имеющих одну и ту же частоту 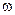 , но разные амплитуды и начальные фазы.
, но разные амплитуды и начальные фазы.
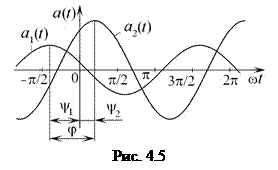 Разность начальных фаз таких функций
Разность начальных фаз таких функций
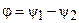
называется фазовым сдвигом между функциями.
Если фазовый сдвиг положителен 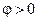 , то говорят, что функция
, то говорят, что функция  опережает по фазе функцию
опережает по фазе функцию 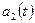 , а если отрицателен
, а если отрицателен 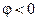 , то — функция
, то — функция 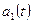 отстаёт по фазе от функции
отстаёт по фазе от функции 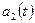 .
.
Если фазовый сдвиг равен нулю 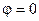 , то говорят, что функции
, то говорят, что функции 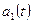 и
и 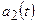 совпадают по фазе и изменяются синфазно. Поэтому такие функции называются синфазными.
совпадают по фазе и изменяются синфазно. Поэтому такие функции называются синфазными.
Если фазовый сдвиг равен 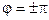 , то говорят, что функции
, то говорят, что функции 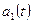 и
и 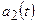 противоположны по фазе. В этом случае функции называются противофазными.
противоположны по фазе. В этом случае функции называются противофазными.
Действующим значением периодической функции 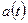 называется среднеквадратическое значение этой функции за период T
называется среднеквадратическое значение этой функции за период T
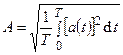
Определим действующее значение гармонической функции (4.4), полагая её начальную фазу равной нулю 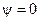
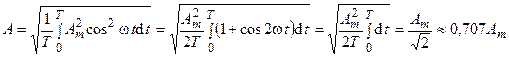 . (4.5)
. (4.5)
Выражая амплитуду 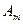 через действующее значение
через действующее значение 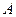 , получаем другую форму записи гармонической функции
, получаем другую форму записи гармонической функции
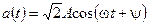 .
.
С энергетической точки зрения действующее значение периодически изменяющегося тока численно равно значению постоянного тока, при протекании которого по сопротивлению 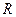 за один период
за один период 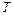 выделится такое же количество тепловой энергии, как при протекании периодического тока. Аналогичное определение может быть дано действующему значению периодически изменяющегося напряжения
выделится такое же количество тепловой энергии, как при протекании периодического тока. Аналогичное определение может быть дано действующему значению периодически изменяющегося напряжения
