Комплексные числа и действия над ними
Комплексным числом 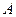 в алгебраической форме записи называется выражение вида
в алгебраической форме записи называется выражение вида
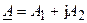 . (4.1)
. (4.1)
где 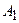 и
и 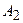 — вещественная и мнимая составляющие комплексного числа, которые могут быть записаны в виде
— вещественная и мнимая составляющие комплексного числа, которые могут быть записаны в виде 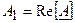 и
и 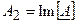 соответственно;
соответственно; 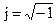 — мнимая единица.
— мнимая единица.
 Комплексное число
Комплексное число 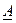 может быть изображено графически в виде точки
может быть изображено графически в виде точки 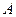 на плоскости в прямоугольной системе координат, у которой по оси абсцисс откладывается вещественная часть
на плоскости в прямоугольной системе координат, у которой по оси абсцисс откладывается вещественная часть 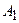 , а по оси ординат — мнимая часть
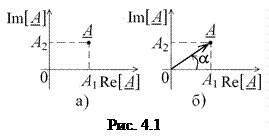
, а по оси ординат — мнимая часть 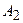 комплексного числа (рис. 4.1, а). В этом случае плоскость называется комплексной, ось абсцисс — вещественной осью, а ось ординат — мнимой осью.
комплексного числа (рис. 4.1, а). В этом случае плоскость называется комплексной, ось абсцисс — вещественной осью, а ось ординат — мнимой осью.
Если точке 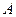 поставить в соответствие вектор, проведённый из начала координат в эту точку (рис. 4.1, б), то полученная диаграмма называется векторной диаграммой комплексного числа
поставить в соответствие вектор, проведённый из начала координат в эту точку (рис. 4.1, б), то полученная диаграмма называется векторной диаграммой комплексного числа 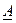 . Величина
. Величина 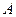 , равная длине вектора
, равная длине вектора 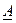 , называется модулем комплексного числа
, называется модулем комплексного числа
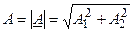 , (4.2)
, (4.2)
а угол наклона 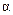 вектора
вектора 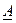 относительно положительной вещественной полуоси называется аргументом комплексного числа
относительно положительной вещественной полуоси называется аргументом комплексного числа 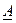 .
.
За положительное направление отсчета аргумента 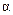 принимается направление против часовой стрелки. Главное значение аргумента
принимается направление против часовой стрелки. Главное значение аргумента 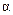 определяется на интервале [
определяется на интервале [ 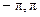 ].
].
Тогда вещественная и мнимая составляющие комплексного числа определяются в виде:
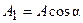 ;
;
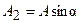 .
.
где
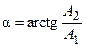 . (4.3)
. (4.3)
Подставляя полученные выражения в (4.1), получаем тригонометрическую форму записи комплексного числа
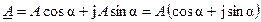 .
.
Используя формулу Эйлера 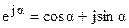 , можно тригонометрическую форму записи комплексного число
, можно тригонометрическую форму записи комплексного число 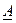 преобразовать в показательную форму
преобразовать в показательную форму
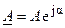 ,
,
где е — основание натурального логарифма.
Два комплексных числа 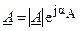 и
и 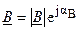 равны, если равны их вещественные и мнимые чисти
равны, если равны их вещественные и мнимые чисти 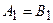 и
и 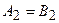 , или, если равны их модули
, или, если равны их модули 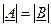 , а аргументы удовлетворяют условию
, а аргументы удовлетворяют условию 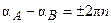 , где
, где 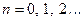 .
.
Два комплексных числа называются комплексно-сопряженными, если их вещественные части равны, а мнимые части отличаются только знаком. Тогда алгебраическая форма записи комплексно сопряженных чисел имеет вид 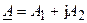 и
и 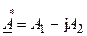 , а показательная —
, а показательная — 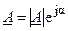 и
и 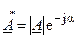 , где символ «*» означает комплексное сопряжение.
, где символ «*» означает комплексное сопряжение.
Сумма двух комплексно сопряженных чисел является действительным числом 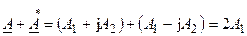 , равным удвоенной вещественной составляющей.
, равным удвоенной вещественной составляющей.
Понятия "больше" и "меньше" применимы только для сравнения модулей и аргументов комплексных чисел, а также их вещественных и мнимых составляющих и не применимы к самим комплексным числам.
Арифметические действия над комплексными числами выполняются аналогично действиям с действительными числами.
Умножение комплексного числа 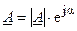 на действительное число
на действительное число 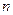 вызывает изменение только модуля комплексного числа в
вызывает изменение только модуля комплексного числа в 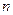 раз
раз 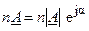 , что эквивалентно изменению длины вектора
, что эквивалентно изменению длины вектора 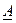 (рис. 4.1) в
(рис. 4.1) в 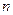 раз.
раз.
Умножение комплексного числа 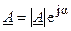 на комплексное число
на комплексное число 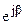 , модуль которого равен
, модуль которого равен 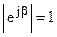 , изменяет только аргумент комплексного числа на
, изменяет только аргумент комплексного числа на 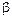 , что эквивалентно повороту вектора
, что эквивалентно повороту вектора 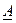 на комплексной плоскости (рис. 4.1, б) на угол
на комплексной плоскости (рис. 4.1, б) на угол 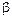 ,
,
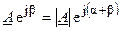 .
.
Тогда умножение комплексного числа на 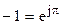 эквивалентно повороту вектора
эквивалентно повороту вектора 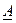 на угол
на угол 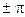 , а умножение на
, а умножение на 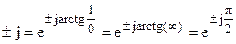
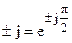 — повороту вектора
— повороту вектора 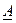 на угол
на угол 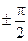 .
.
Поскольку модуль комплексного числа 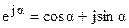 в соответствии с (4.2) равен
в соответствии с (4.2) равен
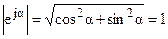 ,
,
то на комплексной плоскости это число изображается в виде единичного вектора, длина которого равна единице, повернутого относительно вещественной оси на угол 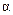 .
.
В теории функций комплексной переменной широкое применение находит показательная функция 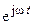 , модуль которой также равен единице
, модуль которой также равен единице 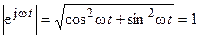 , а аргумент является линейной функцией времени
, а аргумент является линейной функцией времени 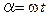 . В случае
. В случае 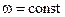 функция
функция 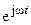 изображается на комплексной плоскости в виде вектора единичной длины, вращающегося вокруг начала координат с угловой скоростью
изображается на комплексной плоскости в виде вектора единичной длины, вращающегося вокруг начала координат с угловой скоростью 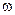 . Поэтому функцию
. Поэтому функцию 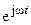 называют оператором вращения.
называют оператором вращения.
