Предмет курса «Процессы и аппараты»

Предмет курса «Процессы и аппараты»

В химической промышленности осуществляются разнообразные процессы, в которых исходные материалы в результате химического взаимодействия претерпевают глубокие превращения, сопровождающиеся изменением агрегатного состояния, внутренней структуры и состава вещества. Наряду с химическими реакциями, являющимися основой химико-технологических процессов, последние обычно включают многочисленные физические, механические и физико-химические процессы.

Таким образом, технология производства самых разнообразных химических продуктов и материалов (кислот, щелочей, полимерных и синтетических материалов) включает ряд однотипных физических и физико-химических процессов, характеризуемых общими закономерностями. Эти процессы в различных производствах проводятся в аналогичных по принципу действия машин и аппаратах.

В курсе «Процессы и аппараты» изучаются теория основных процессов, принципы устройства и методы расчета аппаратов и машин, используемых для проведения этих процессов. Анализ закономерностей протекания основных процессов и разработка обобщённых методов расчёта аппаратов производятся, исходя из фундаментальных законов физики, химии, физической химии, термодинамики, экономики и других наук. Курс строится на основе выявления аналогии внешне разнородных процессов и аппаратов независимо от отрасли химической промышленности.

Таким образом, курс «Процессы и аппараты» является инженерной дисциплиной, представляющей собой важный раздел теоретических основ химической технологии.

Возникновение и развитие науки о процессах и аппаратах

Химическая промышленность начала создаваться на рубеже ХVIII и ХIХ веков и за исторически короткий период, насчитывающий всего 120-150 лет, превратилась в развитых странах в одну из основных ведущих отраслей хозяйства.

В нашей стране идея об общности ряда основных процессов и аппаратов, применяемых в различных химических производствах, была высказана профессором Ф.А. Денисовым ещё в 1828г. Основанная на этой идее новая учебная дисциплина по расчёту и проектированию основных процессов и аппаратов была введена профессором А.К. Крупским в конце 90-х годов прошлого века в Петербургском технологическом институте и несколько позднее профессором И.А. Тищенко в Московском Высшем техническом училище. Большой вклад в науку внесли советские учёные К.Ф. Павлов, А.Г. Касаткин, И.И. Чернобыльский и многие др.

Гидромеханика

Многие технологические процессы химической промышленности связаны с движением жидкостей, газов или паров, перемешиванием в жидких средах, а также с разделением неоднородных смесей путем отстаивания, фильтрования и центрифугирования. Скорость всех указанных физических процессов определяется законами гидромеханики.

Законы гидромеханики подразделяются на: гидростатика – рассматривает законы равновесия в состоянии покоя, и гидродинамика – законы движения жидкостей и газов.

Гидродинамика

Движущей силой при течении жидкостей является разность давлений, которая создается с помощью насосов или компрессоров либо вследствие разности уровней или плотностей жидкости. Различают внутреннюю и внешнюю задачи гидродинамики.

Уравнение Бернулли

Решение уравнений движения Эйлера для установившегося потока приводит к одному из наиболее важных и широко используемых уравнений гидродинамики – уравнению Бернулли.

Для двух поперечных сечений 1 и 2 потока

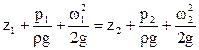(1)

Уравнение Бернулли для идеальной жидкости.

1 – называют полным гидродинамическим напором.

Следовательно, согласно уравнению Бернулли, для всех поперечных сечений установившегося потока идеальной жидкости величина гидродинамического напора остается неизменной.

z – нивелирная высота, называемая также геометрическим напором, представляет собой удельную потенциальную энергию положения в данной точке.

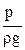– статический или пьезометрический напор, характеризует удельную потенциальную энергию давления в данной точке.

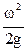– скоростной или динамический напор, характеризует удельную кинетическую энергию в данной точке.

Уравнение Бернулли является частным случаем закона сохранения энергии и выражает энергетический баланс потока.

Уравнение Бернулли реальных жидкостей

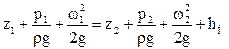
где h_П – потерянный напор, характеризует удельную энергию, расходуемую на преодоление гидравлического сопротивления при движении реальной жидкости.

Основы теории подобия

Модель – упрощенное представление о явлениях, происходящих в естественной природе и сохраняющая основные черты происходящего.

Безразмерные масштабные множители, выражающие отношения однородных сходственных величин подобных фигур (или систем), называются константами подобия.

Инвариантом подобия называют безразмерные отношения каких-либо двух размеров одной из фигур, равные отношению сходственных размеров подобной фигуры.

Геометрическое подобие соблюдается при равенстве отношений всех сходственных линейных размеров натуры и модели:

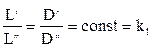
Временное подобие характеризуется тем, что сходственные частицы в геометрически подобных системах, двигаясь по геометрически подобным траекториям, проходят геометрически подобные пути за промежутки времени, отношение которых является постоянной величиной:

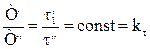
Подобие физических величин предполагает, что для двух сходственных точек, размещенных подобно в пространстве и времени, отношения физических свойств является величинами постоянными:

Первая теорема подобия была сформулирована Ньютоном. Согласно этой теореме, при подобии систем всегда могут быть найдены такие безразмерные комплексы величин, которые для сходственных точек данных систем одинаковы, т.е. подобные явления характеризуются численно равными критериями подобия.

Второй закон Ньютона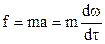

Выделим в подобных системах 2 частицы, движущиеся подобно. В натуре на частицу массой 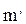действует сила 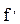сообщая ей ускорение 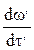; в модели сходственная частица массой 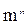под действием силы 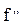приобретает ускорение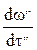

Тогда

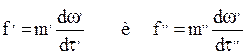
При подобном движении частиц для сходственных точек натуры и модели константы подобия выражаются отношениями:

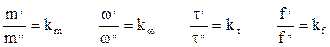
т.е.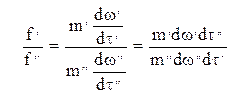

Отношения приращений величин, входящих в константы подобия, можно заменить отношениями самих величин, т.е.

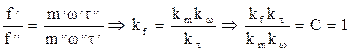
Величину С, составленную их констант подобия, называют индикатором подобия.

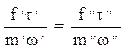
Таким образом, получен безразмерный комплекс величин, значения которого одинаковы для сходственных точек обеих систем. Этот комплекс называют критерием Ньютона

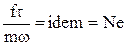
который характеризует отношение действующей на частицу силы к силе инерции.

Достоинства критериев – не имеют размерности и позволяют удобно моделировать процессы упрощенно.

Вторая теорема подобия была доказана Бэкингемом, Федерманом и Афанасьевой-Эренфест. Согласно этой теореме, решение любого дифференциального уравнения, связывающего между собой переменные, влияющие на процесс, может быть представлено в виде зависимости между безразмерными комплексами этих величин, т.е. между критериями подобия.

Если обозначить критерии подобия через 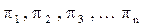, то решение дифференциального уравнения может быть представлено в общем виде:

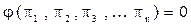
Такие уравнения называют уравнениями в обобщенных переменных или критериальными уравнениями.

Критерии подобия, которые составлены только из величин, входящих в условия однозначности, называют определяющими. Критерии же, включающие также величины, которые не являются необходимыми для однозначной характеристики данного процесса, а сами зависят от этих условий, называют определяемыми.

Из критериального уравнения, представляющего собой функциональную зависимость между критериями подобия, рассчитав предварительно величины определяющих критериев, находят величину определяемого критерия, а из него – численное значение интересующей нас величины. Если определяемым является некоторый критерий π₁ , то .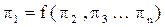

Вторая теорема подобия отвечает на вопрос, как обрабатывать результаты опытов, проведенных на моделях: их надо представлять в виде функциональной зависимости между критериями подобия.

Третья теорема подобия, или теорема М.В.Кирпичева и А.А. Гухмана, формулирует необходимые и достаточные условия подобия: подобны те явления, которые описываются одной и той же системой дифференциальных уравнений и у которых соблюдается подобие условий однозначности.

Таким образом, исследование процессов методом теории подобия должно состоять из следующих элементов:

1. Получив полное математическое описание процесса, т.е. составив дифференциальное уравнение и установив условия однозначности, проводят подобное преобразование этого уравнения и находят критерии подобия.

2. Опытным путем на моделях устанавливают конкретный вид зависимости между критериями подобия, причем полученное обобщенное расчетное уравнение справедливо для всех подобных явлениях в исследованных пределах.

Движение тел в жидкости

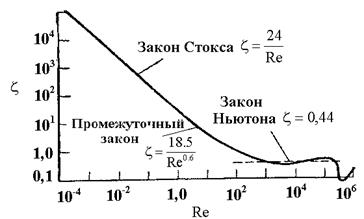
При движении тела в жидкости возникают сопротивления, для преодоления которых и обеспечения равномерного движения тела должна быть затрачена определенная энергия. Величина возникающего сопротивления зависит главным образом от режима движения и формы обтекаемого тела.

При ламинарном режиме тело окружено пограничным слоем жидкости и плавно обтекается потоком. Потеря энергии связана с преодолением сопротивления трения. С развитием турбулентности потока все большую роль начинают играть силы инерции. Сила сопротивления R среды движущемуся в ней телу выражена уравнением сопротивления:

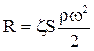(1)

где S – площадь проекции тела на плоскость, перпендикулярную направлению его движения, м² ;

ζ – коэффициент сопротивления среды.

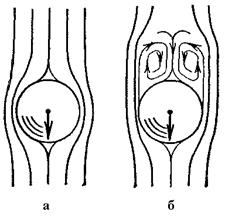а – ламинарный поток

б – турбулентный поток

Отношение R/S представляет собой перепад давлений Δр (Н/м²), преодолеваемый движущимся телом.

Ламинарный режим закон Стокса Re < 2

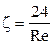
Переходный режим Re = 2 – 500

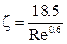
Автомодельный режим закон Ньютона ~ 2·10⁵ > Re < ~ 500

ζ = 0,44 = const

Постановка в уравнение (1) каждого из приведённых выше уравнений для ζ показывает, что для ламинарного режима Re ~ ω для переходного режима Re ~ ω^1,4 , для автомодельного режима Re ~ ω²

Для тел по форме отличных от шарообразных значения коэффициента сопротивления зависит от фактора формы Ф и числа Рейнольдса.

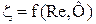здесь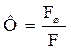

где F_ш – поверхность шара, имеющего тот же объём, что и рассматриваемое тело поверхностью F. Например, для куба Ф = 0,806; для цилиндра высотой, в 10 раз превышающей его радиус, Ф = 0,69.

Закон внутреннего трения Ньютона, согласно которому напряжение внутреннего трения, возникающее между слоями жидкости при её течении, прямо пропорционально градиенту скорости.

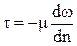кажущейся вязкостью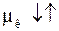

где μ – динамический коэффициент вязкости;

τ – касательное напряжение, напряжение внутреннего трения.

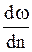– градиент скорости.

Жидкости, подчиняющиеся закону внутреннего трения Ньютона называются нормальными, или ньютоновскими. Однако в промышленной практике приходится иметь дело и с неньютоновскими жидкостями (растворы многих полимеров, густые суспензии, пасты (бингамовские пластичные, псевдопластичные, дилатантные и др.)

Разделение жидких систем

Материальный баланс процесса разделения

Введем обозначения:

G_см , G_осв , G_ос – количество исходной смеси, осветленной жидкости и получаемого осадка, кг;

х_см , х_осв , х_ос – содержание дисперсной фазы в исходной смеси, осветленной жидкости и осадке, массовые доли, кг а/кг (а+b).

При отсутствии потерь вещества в процессе разделения уравнения материального баланса имеют вид:

по общему количеству веществ

(1)

по дисперсной фазе

(2)

Совместное решение уравнений (1) и (2) позволяет определить:

Отстаивание

Скорость стесненного осаждения. Отстойники.

Опыт показывает, что при отстаивании наблюдается постепенное увеличение концентрации диспергированных частиц в аппарате по направлению сверху вниз.

Схема процесса отстаивания

Зависимость скорости отстаивания от времени

1 – слой осадка (шлама); 2 – зона сгущенной суспензии; 3 – зона свободного осаждения (коллективное); 4 – осветленная жидкость.

В начале осаждаются более крупные частицы, вызывающие наиболее интенсивное обратное движение жидкости. Однако по мере уменьшения концентрации этих частиц тормозящее влияние обратного тока жидкости ослабевает и скорость отстаивания возрастает (аb) до момента установления динамического равновесия между действующей силой (весом) и силой сопротивления среды. В последующий период совместного осаждения частиц происходит с постоянной скоростью (bс). Завершающая и наиболее медленная стадия процесса – уплотнение осадка. Частицы располагаются настолько близко друг от друга, что вытеснение жидкости становится все более затруднительным – здесь происходит уменьшение скорости осаждения (сd).

Различают аппараты периодического, непрерывного и полунепрерывного действия.

Периодически действующие отстойники представляют собой низкие бассейны без перемешивающих устройств. После того как произойдет разделение слой осветленной жидкости декантируют, т.е. сливают через сифонную трубку или краны, расположенные выше уровня осевшего осадка. Размеры и форма аппаратов зависят от концентрации диспергированной фазы и размеров ее частиц (крупные частицы – меньше диаметр, скорость осаждения обратно пропорциональна вязкости, которая уменьшается с увеличением температуры) коническое днище.

Полунепрерывный способ – жидкость поступает и удаляется непрерывно, а осадок выгружается из аппарата периодически – бетонные бассейны.

Отстойники полунепрерывного действия с наклонными перегородками

1 – штуцер для ввода исходной суспензии; 2 – корпус; 3 – наклонные перегородки, которые увеличивают время пребывания жидкости и поверхность осаждения в аппарате; 4 – бункера для осадка; 5 – штуцер для непрерывного отвода осветленной жидкости.

Отстойник непрерывного действия с гребковой мешалкой

1 – корпус; 2 – кольцевой желоб; 3 – мешалка; 4 – лопасти с гребками; 5 – труба для подачи исходной суспензии; 6 – штуцер для вывода осветленной жидкости; 7 – разгрузочное устройство для осадка; 8 – электродвигатель.

Мешалка делает 0,015 до 0,5 об/мин. Осадок – текучая сгущенная суспензия (с концентрацией твердой фазы 35 – 55%) удаляется с помощью диафрагмового насоса. Осадок направляется во второй отстойник для отмывки водой и последующего отстаивания. Осадок, полученный во втором аппарате, будет содержать такое же количество жидкости, что и осадок в первом отстойнике, но уже значительно разбавленный водой. При наличии нескольких последовательно соединенных отстойников можно удалить из осадка до 97 –

98 % жидкости.

Схема непрерывной противоточной отмывки осадка от жидкости

Гребковые отстойники обладают следующими достоинствами: большая производительность (иногда 3000 т/сутки осадка), равномерная плотность осадка, обеспечивается более эффективное обезвоживание осадка. К недостаткам можно отнести их громоздкость (d = от 1,8 до 30м, иногда 100м).

Многоярусные отстойники (закрытого и сбалансированного типа)

1 – распределитель исходной смеси; 2 – труба – стакан для ввода суспензии в каждый ярус; 3 – коллектор для сбора осветленной жидкости; 4 – сборник осадка.

В местах прохода вала сквозь днище каждого отстойника установлены уплотняющие сальники.

Отстойники проектируются в расчете на осаждение самых мелких частиц, находящихся в исходной смеси.

Пусть за время τ (сек) суспензия разделяется на слой сгущенной суспензии и слой осветленной жидкости высотой h (м). При поверхности осаждения F (м²) объем осветленной жидкости, получаемой в единицу времени, V_осв (м³/сек):

(1)

За то же время частицы, осаждающиеся со скоростью ω_ст , должны проходить путь h (м):

(2)

Подставив (2) в (1) получим:

Производительность отстойника зависит от скорости и поверхности осаждения.

Высота отстойника – 1,8 – 4,5 м.

Необходимую поверхность осаждения находим из выражения:

(3)

, тогда: (4)

Фильтрование

При этом суспензия разделяется на чистый фильтрат и влажный осадок.

Разность давлений по обе стороны фильтровальной перегородки создают разными способами, в результате чего осуществляют различные процессы фильтрования.

Если пространство над суспензией сообщают с источником сжатого газа или пространство под фильтровальной перегородкой присоединяют к источнику вакуума, то происходит процесс фильтрования при постоянной разности давлений.

Если суспензию подают на фильтр поршневым насосом, производительность которого при данном числе оборотов электродвигателя постоянная, то осуществляется процесс фильтрования при постоянной скорости.

Если суспензию транспортируют на фильтр центробежным насосом, производительность которого при данном числе оборотов электродвигателя уменьшается при возрастании сопротивления, осадка, что обуславливает повышение разности давлений, то производится процесс фильтрования при переменных разности давлений и скорости.

Процесс фильтрования может идти: с образованием осадка, с закупориванием пор, промежуточный вид.

При разделении суспензий с небольшой концентрацией тонкодисперсной твердой фазы часто применяют фильтровальные вспомогательные материалы: перлит, диатомит, асбест, целлюлозу, древесную муку (не более 50 мм).

Осадки, получаемые на фильтровальной перегородке при разделении суспензий, подразделяют на несжимаемые и сжимаемые. Под несжимаемыми понимают такие осадки, в которых пористость, т.е. отношение объема пор к объему осадка, не уменьшается при увеличении разности давлений (неорганические вещества размером более 100 мкм) (к сильно сжимаемым относятся осадки гидратов окисей металлов – алюминия, меди).

Промывка, продувка и сушка осадка.

Промывку выполняют двумя способами – вытеснения и разбавления.

Продувка. Часть жидкости из пор до достижения равновесной влажности.

Сушка – получить осадок с окончательной влажностью менее равновесной.

Уравнения фильтрования

Скорость процесса пропорциональна движущей силе и обратно пропорциональна сопротивлению. Т.к. в процессе фильтрования значения разности давлений и гидравлического сопротивления мешаются, то переменную скорость фильтрования (м/сек) выражают в дифференциальной форме:

где V – объем фильтрата, м³;

S – поверхность фильтрования, м²;

Δр – разность давлений, Н/м²;

μ – вязкость жидкой фазы суспензии, Н·сек/м².

где r₀ – удельное объемное сопротивление слоя осадка, м^-2, характеризует сопротивление, оказываемое потоку жидкой фазы равномерным слоем осадка толщиной 1м;

х₀ – отношение объема осадка и объему фильтрата.

и то, что равномерного слоя осадка по перегородке:

таким образом, удельное сопротивление осадка численно равно разности давлений, необходимой для того, чтобы жидкая фаза с вязкостью 1Н·сек/м² фильтровалась со скоростью 1м/сек сквозь слой осадка толщиной 1м.

V = 0 в начале

Уравнение фильтрования при постоянной разности давлений, Δp = сonst:

Уравнение фильтрования при постоянной скорости процесса, W = const:

Уравнение фильтрования при постоянных разности давлений и скорости:

Если чистая жидкость фильтруется через слой осадка постоянной толщины.

Определение постоянных в уравнениях фильтрования. Преобразуя уравнение фильтрования при постоянной разности давлений:

(3)

где (1)

(2)

При Δp = const и t = const все величины входящие в правые части равенства (1) и (2) постоянны.

Тогда выражение (3) является уравнением прямой линии, наклоненной к горизонтальной оси под углом, тангенс которого равен М, и отсекающей на оси ординат отрезок N.

+++++++++++++++ +++++++++++++++++++ +++++++++++

Направление фильтрования

Взаимные направления действия силы тяжести и движения фильтрата в фильтрах

а – направления совпадают; б – направления противоположны; в – направления перпендикулярны; сплошные стрелки – направление действия силы тяжести; пунктирные стрелки – направление движения фильтрата; 1 – фильтровальная перегородка; 2 – осадок; 3 – суспензия; 4 – фильтрат; 5 – чистая жидкость.

Уравнение при ΔP = const

Т_фильт = const, все величины за исключением V и τ постоянны.

Проинтегрируем:

или

Разделим обе части уравнения на

Из уравнения следует, что по мере увеличения объема фильтрата, а следовательно, и продолжительности фильтрования скорость фильтрования уменьшается.

+++++++++++++++ +++++++++++++++++++ +++++++++++

Расчет фильтров

Периодически действующие фильтры

1. Определение τ_осн при условии, что промывка и продувка отсутствует, а разделение происходит при ΔP = const

2. Определение объема фильтрата:

3. Общее число циклов работы фильтра в сутки

где Q_общ. – производительность установки по фильтрату.

4. Число циклов работы одного фильтра в сутки

5. Необходимое количество фильтров:

Непрерывно действующие фильтры

1. Принимают оптимальную толщину осадка ~ 5 мм.

2. Из равенства находят:

3. Определяем время фильтрования из условия R_фп = 0:

4. Опытным путем определяем продолжительность стадии промывки τ_п

5. Число секций в зоне первого обезвоживания , второго обезвоживания , удаление осадка и регенерации

6. Продолжительность:

– первое обезвоживание

где – число секций в зонах фильтрования и промывки.

– второе обезвоживание

– удаление осадка и регенерации

7. Общая продолжительность цикла:

8. Скорость вращения барабана:

Центрифугирование

Под центрифугированием понимают процесс разделения неоднородных систем, в частности эмульсий, суспензий, в поле центробежных сил с использованием сплошных или проницаемых для жидкости перегородок.

Центрифуга представляет собой в простейшем виде вертикальный цилиндрический ротор со сплошными или перфорированными стенками. Ротор укрепляется на вертикальном валу, который приводится во вращение электродвигателем, помещается в соосный цилиндрический неподвижный кожух, закрываемый съемкой крышкой; на внутренней поверхности ротора с перфорированными стенками находится фильтровальная ткань или тонкая металлическая сетка.

Под действием центробежных сил суспензия разделяется на осадок и жидкую фазу, называемую фугатом. Осадок остается в роторе, а жидкая фаза удаляется из него.

В отстойных центрифугах со сплошными стенками производят разделение эмульсий и суспензий по принципу отстаивания, причем действие силы тяжести заменяется действием центробежной силы.

В фильтрующих центрифугах с проницательными стенками осуществляют процесс разделения суспензий по принципу фильтрования, причем вместо разности давлений используется действие центробежной силы (пример: отделение маточного раствора от нитрозофенола).

В отстойной центрифуге разделяемая суспензиями или эмульсия отбрасывается центробежной силой и стенкам ротора, причем жидкая или твердая фаза с большей плотностью располагается ближе к стенкам ротора, а другая фаза с меньшей плотностью размещается ближе к его оси; осадок (или фаза с большей плотностью) образует слой у стенок ротора, а фугат переливается через верхний край ротора.

В фильтрующей центрифуге разделяемая суспензия также отбрасывается к стенкам ротора и фазы разделяются; при этом жидкая фаза проходит сквозь фильтровальную перегородку в кожух и отводится из него, твердая фаза в виде осадка задерживается на внутренней стороне этой перегородки, а затем удаляется из ротора.

Разделение эмульсий в отстойных центрифугах обычно называют сепарацией, а устройства, в которых осуществляется этот процесс – сепараторами (отделение сливок от молока, маточного раствора от нитрозофенало).

Центробежная сила и фактор разделения

В общем случае величина центробежной силы выражается равенством:

где С – центробежная сила, Н;

m – масса вращающегося тела, кг;

G – вес вращающегося тела, Н;

ω – окружная скорость вращения, м/сек;

r – радиус вращения, м.

Окружная скорость вращения определяется равенством:

где ω^, – угловая скорость вращения, рад/сек.

n – число оборотов в минуту.

Сопоставив эти два равенства, получим:

Увеличение числа оборотов ротора значительно больше влияет на возрастание центробежной силы, чем увеличение диаметра ротора центрифуги.

Отношение центробежного ускорения ω²/r к ускорению силы тяжести g называют фактором разделения:

Приняв G = 1 Н, получим:

С диаметром ротора 1000 мм (r = 0,5 м), вращающийся со скоростью n = 1200 об/мин:

Устройство центрифуг

По величине фактора разделения центрифуги можно условно разделить на две группы: нормальные центрифуги (К_р < 3500) и сверхцентрифуги (К_р >3500).

Нормальные центрифуги применяются главным образом для разделения различных суспензий, за исключением суспензий с очень малой концентрацией твердой фазы.

Сверхцентрифуги являются аппаратами отстойного типа и подразделяются на трубчатые сверхцентрифуги, используемые для разделения тонкодисперсных суспензий, и жидкостные сепараторы, служащие для разделения эмульсий.

По расположению оси вращения различают: вертикальные, наклонные и горизонтальные центрифуги.

Жидкостные сепараторы. Эти аппараты являются отстойными сверхцентрифугами непрерывного действия с вертикальным ротором.

Диаметр ротора 150 – 300 мм, вращается со скоростью 5000 – 10000 об/мин.

В жидкостном сепараторе тарельчатого типа обрабатываемая смесь в зоне отстаивания разделена на несколько слоев. Эмульсия подается по центральной трубе 1 в нижнюю часть ротора, откуда через отверстия в тарелках 2 разделяется тонкими слоями между ними. Более тяжелая жидкость, перемещаясь вдоль поверхности тарелок, отбрасывается центробежной силой к периферии ротора и отводится через отверстие 3. Более легкая жидкость перемещается к центру ротора и удаляется через кольцевой канал 4. Для того чтобы жидкость не отставала от вращающегося ротора, он снабжен ребрами 5.

1 – труба для подачи эмульсии; 2 – тарелки; 3 – отверстие для отвода более тяжелой жидкости; 4 – кольцевой канал для отвода более легкой жидкости; 5 – ребра.

Схема устройства трубчатой сверхцентрифуги

1 – кожух; 2 – ротор; 3 – радиальные лопасти; 4 – шпиндель; 5 – опора; 6 – шкив; 7 – подпятник; 8 – труба для подачи суспензии; 9 – отверстия; 10 – труба для отвода осветленной жидкости.

Трубчатые сверхцентрифуги. По сравнению с жидкостными сепараторами трубчатые центрифуги имеют ротор меньшего диаметра (не более 200 мм), вращающийся с большей скоростью (45000 об/мин); фактор разделения 15000. Применяется для осветления лаков.

В кожухе 1 расположен ротор 2, с глухими стенками, внутри которого имеются радиальные лопасти 3, препятствующие отстаиванию жидкости от стенок ротора при его вращении. Верхняя часть ротора жестко соединена с коническим шпинделем 4, который подвешен на опоре 5 и приводится во вращение при помощи шкива 6. В нижней части ротора расположен эластичный направляющий подпятник 7, через который проходит труба 8 для подачи суспензии. При движении суспензии в роторе вверх на стенках его оседают твердые частицы, причем осветленная жидкость отводится через отверстия 9 в трубу 10. По истечении определенного времени сверхцентрифугу останавливают и удаляют осадок, накопившийся в роторе.

Разделение газовых систем: гравитационную очистку газов – пылеосадительные камеры мокрая очистка – полые и насадочные скрубберы. Трехколонные центрифуги. Подвесные центрифуги, горизонтальные центрифуги с ножевым устройством для удаления осадка, центрифуги со шнековым устройством для удаления осадка, центрифуги с инерционной выгрузкой осадка.

Угол трения частиц осадка меньше, чем угол наклона стенок ротора и поэтому они перемещаются к его нижнему краю, непрерывного действия. Тормозится шнеком.

Центрифугирование

Образуются слои с цилиндрическими граничными поверхностями, что усложняет зависимость процесса от геометрических факторов.

Отстойные центрифуги

центробежные осветление

центробежное отстаивание

Осаждение → по законам гидродинамики.

Уплотнение осадка → по закономерностям механики грунтов.

При концентрации менее 4% оборотов нет четкой границы.

В отстойниках гравитационное поле однородно, центробежная сила увеличивается при движении к периферии.

Разделяющая способность отстойных центрифуг характеризуется индексом производительности:

где F – площадь цилиндрической поверхности осаждения.

Индекс производительности отражает влияние всех конструктивных особенностей осадительной центрифуги, определяющих ее разделительную способность.

Рассмотрим цилиндрический ротор центрифуги. h << D ротора. Поэтому величину фактора разделения можно отнести к среднему диаметру (D – h).

Площадь цилиндрической поверхности осаждения в роторе: