Расчет параметров и характеристик модели множественной регрессии

Параметры уравнения множественной регрессии оцениваются, как и в парной регрессии, МНК. При его применении строится система нормальных уравнений, решение которой позволяет получить оценки параметров регрессии.

Для уравнения система нормальных уравнений составит:

При нелинейной регрессии, приводимой к линейному виду, ее параметры также можно определить МНК с той лишь разницей, что он используется не к исходной информации, а к преобразованным данным.

Ценность эконометрических моделей состоит в том, что они позволяют не только выявить связи и зависимости, выразить их на языке математики, дать экономическое истолкование параметрам, но и в том, что позволяют рассчитать ряд характеристик.

Наиболее важными из них являются следующие:

· предельная эффективность показателя-фактора;

· коэффициент эластичности;

· изокванта;

· предельная норма заменяемости одного фактора другим;

· изоклинал;

· индексы корреляции и детерминации;

· стандартная ошибка и другие.

Рассмотрим сущность и методику расчета каждого из перечисленных характеристик.

Предельная эффективность показывает - на сколько абсолютных единиц измениться результативный показатель, если данный фактор увеличиться на одну абсолютную единицу, а остальные факторы останутся неизменными. Предельная эффективность представляет собой частную производную по показателю-фактору, т.е. где i = 1,2,…,n.

Коэффициент эластичности показывает - на сколько процентов измениться результативный показатель, если данный показатель-фактор измениться на один процент, а остальные факторы останутся неизменными.

Формула для расчета коэффициента эластичности (Eх_i) имеет вид

.

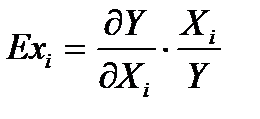Например, для линейной 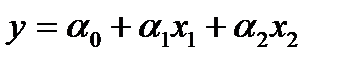и степенной модели 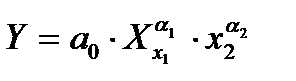предельная эффективность факторов х₁ и х₂ равна соответственно

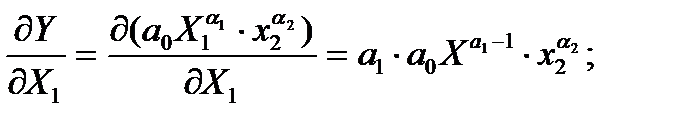
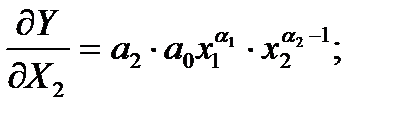
а коэффициент эластичности

.

Следует обратить внимание на следующие частные случаи:

- в случае линейной зависимости предельная эффективность фактора равна коэффициенту регрессии, т.е.

- в случае зависимости степенного вида коэффициент эластичности показателя-фактора равен коэффициенту регрессии, т.е. 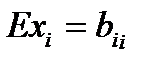, i=1,2,…,n .

Изокванта, предельная норма заменяемости одного фактора другим, изоклинал - характеристики, рассчитываемые только для многофакторных моделей.

Изоквантой называют множество сочетаний значений показателей-факторов, при которых результативный показатель принимает одно и тоже значение. Чтобы найти изокванту надо:

- принять Y за константу (Y= const);

- выразить один из факторов через остальные.

Например, для изоквантой является

или .

Для каждой эконометрической модели можно построить «семейство» изоквант.

Предельная норма заменяемости одного фактора другим позволяет- определить, сколько единиц одного фактора требуется для замены одной единицы другого фактора. Чтобы рассчитать предельную норму заменяемости надо:

- найти изокванту;

- определить частную производную одного фактора по другому, т.е. ¶Х_l/¶Х_k, где l≠k , l и k Î i = 1,2,…,n.

Например, для 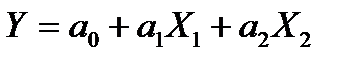предельная норма заменяемости составляет ; .

Изоклинал – это множество сочетаний значений показателей-факторов, при которых предельная норма заменяемости принимает одно и тоже значение. Чтобы найти изоклинал, надо:

- найти предельную норму заменяемости;

- принять предельную норму заменяемости за константу

- выразить один из факторов через остальные.