На любой экономической показатель чаще всего оказывает влияние не один, а несколько факторов.

Парная (однофакторная) регрессия является частным случаем множественной регрессии. Схематически модель множественной регрессии записывается в виде: 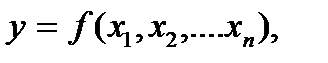где y результативный экономический показатель, 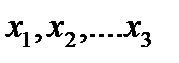- показатели факторы.

Множественная регрессия широко используется в решении проблем спроса, доходности акций, при изучении функций издержек производства, в макроэкономических расчетах и при решении других вопросов в различных экономических сферах. В настоящее время множественная регрессия – один из наиболее распространенных методов в эконометрике.

Основная цель множественной регрессии - построить модель с большим числом факторов, определив при этом влияние каждого из них в отдельности, а также совокупное их воздействие на моделируемый показатель.

Построение уравнения множественной регрессии начинается с решения вопроса о спецификации модели (выбор факторов, вида уравнения и др.)

Факторы, включаемые в модель множественной регрессии, должны отвечать следующим требованиям:

­ должны быть количественно измеримы;

­ не должны быть интеркоррелированы или находится в функциональной зависимости;

­ в одну модель нельзя включать совокупный фактор и образующие его частные факторы, что может привести к неоправданному увеличенному их влияние на зависимый показатель, к искажению реальной действительности;

­ количество включаемых в модель факторов не должно превышать одной трети числа наблюдений в выборке.

Отбор факторов обычно осуществляется в две стадии: на первой подбираются факторы, исходя из сущности проблемы; на второй – на основе матрицы показателей корреляции определяют t - статистики для параметров регрессии.

Коэффициенты интеркорреляции (т.е. корреляции между объясняющими переменными) позволяют исключать из модели дублирующие факторы. Считается, что две переменные явно коллинеарны, т.е. находятся между собой в линейной зависимости, если .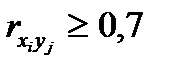

Из двух явно коллинеарных факторов, уравнения регрессии - рекомендуется исключить один. Предпочтение при этом отдается тому фактору, который при достаточно тесной связи с результатом имеет наименьшую тесноту связи с другими факторами.

Рассмотрим пример. Для зависимости 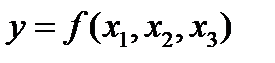задана матрица парных коэффициентов корреляции:

	У	x1	x2	x3
У	1
x1	0,8	1
x2	0,7	0,8	1
x3	0,6	0,5	0,2	1

Из таблицы, очевидно, что факторы 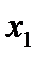и 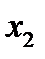коррелированны друг с другом. В уравнение целесообразно включить фактор 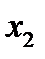, а не 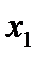, так как корреляция x₂ с y - слабее, чем корреляция фактора x₁ с y 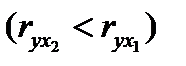,но зато r_x1x3 >r_x2x3 . Поэтому в уравнение множественной регрессии включаются факторы x₂ и x₃.

При отборе влияющих факторов используются статистические методы отбора. Так, существенного сокращения числа влияющих факторов можно достичь с помощью пошаговых процедур отбора переменных. Ни одна их этих процедур не гарантирует получения оптимального набора переменных. Однако при практическом применении они позволяют получить достаточно хорошие наборы существенно влияющих факторов.

Наиболее широкое применение получили следующие методы отбора факторов: метод исключения, метод включения, шаговый регрессионный анализ.

Метод исключенияпредполагает построение уравнения, включающего всю совокупность переменных, с последующим последовательным (пошаговым) сокращением числа переменных в модели до тех пор, пока не выполнится некоторое, наперед заданное, условие. Суть метода включения состоит – в последовательном включении переменных в модель до тех пор, пока регрессионная модель не будет отвечать заранее установленному критерию качества. Последовательность включения определяется с помощью частных коэффициентов корреляции: переменные, имеющие относительно исследуемого показателя большие значения частного коэффициента корреляции, первыми включаются в регрессионное уравнение.

Шаговый регрессионный анализ состоит в исключении ранее введенного фактора. Матрица частных коэффициентов корреляции наиболее широко используется в процедуре отсева факторов.

Уравнения множественной регрессии как парной регрессии могут быть: линейными и нелинейными.

Наиболее часто используются линейная и степенная функции:

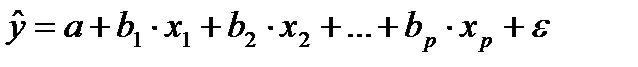- линейная,

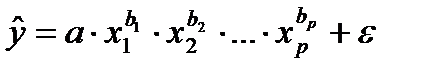- степенная.

Линеаризуемы и широко применяются и следующие уравнения множественной регрессии:

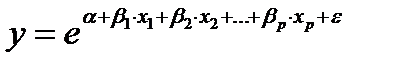- экспоненциального вида:

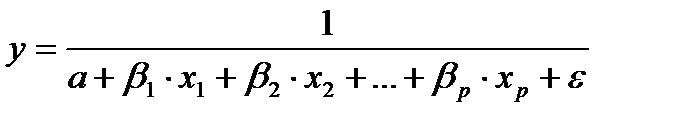гиперболического вида.

В качестве моделей множественной регрессии могут быть использованы и другие виды математических функций, которые могут быть преобразованы к линейному виду, например:

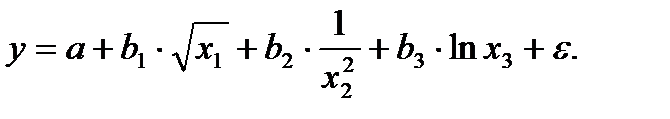
Обозначив ; ; ,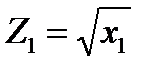

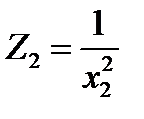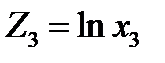получаем линейное уравнение множественной регрессии

.
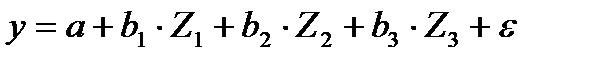