Оценка точности выравнивания
I. Оценка выравнивания линейной зависимости между_______________________________
_____________________________________________________________________________
1. Сравнение исходных данных с вероятными, полученными по управлению, вычисленному методом координат точек
| Данные для сравнения | Мср | 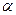 |  | а | а2 | |
| исходные | вероятные (Yв)1 | |||||
_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________
Вывод:_______________________________________________________________________
2. Сравнение исходных данных с вероятными, полученными по уравнению, вычисленному методом наименьших квадратов
| Данные для сравнения | Мср | 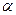| | а | а2 | |
| исходные | вероятные (Yв)2 | |||||
_________________________________________________________________________________________________________________________________________________________
Вывод:_______________________________________________________________________
I. Оценка выравнивания нелинейной зависимости между____________________________
_____________________________________________________________________________
1. Сравнение исходных данных с вероятными, полученными по уравнению, вычисленному методом координат точек
| Данные для сравнения | Мср | 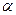| | а | а2 | |
| исходные | вероятные (Yв)1 | |||||
Вывод:_______________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
2. Сравнение исходных данных с вероятными, полученными по уравнению, вычисленному методом наименьших квадратов
| Данные для сравнения | Мср | 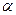| | а | а2 | |
| исходные | вероятные (Yв)2 | |||||
Вывод:_______________________________________________________________________
_____________________________________________________________________________
_____________________________________________________________________________
ДИСПЕРСИОННЫЙ АНАЛИЗ ОДНОФАКТОРНОГО КОМПЛЕКСА
Цель анализа: установить степень и достоверность влияния
1. Построение дисперсионного комплекса
| Повторности опыта | Градации действующего фактора | |||||
| 1 | 2 | 3 | 4 | 5 | итого | |
| Объем выборки по градациям (n) | ||||||
| Сумма вариант по градациям (∑V) | ||||||
| Групповые средние Mr |
2. Вспомогательные расчеты
1. Средний квадрат суммы всех вариант
2. Сумма средних квадратов суммы вариант по градациям комплекса
3. Сумма квадратов всех вариант комплекса
3. Расчет дисперсий:
1. Факториальная:
2. Случайная:
3. Общая
4. Сила влияния и ее достоверность. Расчеты
Сила влияния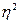 
=
Достоверность силы влияния F=
Расчет варианс:
Случайная: Факториальная
Стандартное значение критерия Фишера FST=
| Число степеней свободы f1= f2= | Ошибка силы влияния и доверительный интервал для генеральной совокупности |
Расчет оптимальной величины действующего фактора:
tst=
Графическое изображение дисперсии
Y
 | ||||||
 | ||||||
| ||||||
| |
Выводы:
1.
2.
3.
РАСЧЕТ ДОСТАТОЧНОГО ЧИСЛА НАБЛЮДЕНИЙ
1. Исходные данные (из задания №2)
1. Изучаемый признак__________________________________________________________
2. Число наблюдений___________________________________________________________
3. Точность опыта______________________________________________________________
4. Коэффициент варьирования (С)________________________________________________
II. Расчет достаточного числа наблюдений при заданной точности опыта
Исходная формула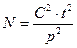 
| Вероятность | Точность | Расчет | Число наблюдений |
| 0,95 (t=2) | |||
| 0,99 (t=3) | |||
| 0,95 (t=2) | |||
| 0,99 (t=3) | |||
Приложение 1
Значения функции f (x)
| σ | ||||||||||
| 0,0 | 1,0 | |||||||||
| 0,1 | ||||||||||
| 0,2 | ||||||||||
| 0,3 | ||||||||||
| 0,4 | ||||||||||
| 0,5 | ||||||||||
| 0,6 | ||||||||||
| 0,7 | ||||||||||
| 0,8 | ||||||||||
| 0,9 | ||||||||||
| 1,0 | ||||||||||
| 1,1 | ||||||||||
| 1,2 | ||||||||||
| 1,3 | ||||||||||
| 1,4 | ||||||||||
| 1,5 | ||||||||||
| 1,6 | ||||||||||
| 1,7 | ||||||||||
| 1,8 | ||||||||||
| 1,9 | ||||||||||
| 2,0 | ||||||||||
| 2,1 | ||||||||||
| 2,2 | ||||||||||
| 2,3 | ||||||||||
| 2,4 | ||||||||||
| 2,5 | ||||||||||
| 2,6 | ||||||||||
| 2,7 | ||||||||||
| 2,8 | ||||||||||
| 2,9 | ||||||||||
| 3,0 | ||||||||||
| 3,1 | ||||||||||
| 3,2 | ||||||||||
| 3,3 | ||||||||||
| 3,4 | ||||||||||
| 3,5 | ||||||||||
| 3,6 | ||||||||||
| 3,7 | ||||||||||
| 3,8 | ||||||||||
| 3,9 | ||||||||||
| 4,0 |
| Приложение 2 | ||||||||
| Таблица площади кривой нормального распределения | ||||||||
| Расстояние от М, в σ | На 10000 | Для 0,01 σ | Расстояние от М, в σ | На 10000 | Для 0,01 σ | Расстояние от М, в σ | На 10000 | Для 0,01 σ |
| 0,00 | 1,30 | 2,60 | ||||||
| 0,05 | 1,35 | 2,65 | ||||||
| 0,10 | 1,40 | 2,70 | ||||||
| 0,15 | 1,45 | 2,75 | ||||||
| 0,20 | 1,50 | 2,80 | ||||||
| 0,25 | 1,55 | 2,85 | ||||||
| 0,30 | 1,60 | 2,90 | ||||||
| 0,35 | 1,65 | 2,95 | ||||||
| 0,40 | 1,70 | 3,00 | - | |||||
| 0,45 | 1,75 | 3,05 | - | |||||
| 0,50 | 1,80 | 3,10 | - | |||||
| 0,55 | 1,85 | 3,15 | - | |||||
| 0,60 | 1,90 | 3,20 | - | |||||
| 0,65 | 1,95 | 3,25 | - | |||||
| 0,70 | 2,00 | 3,30 | - | |||||
| 0,75 | 2,05 | 3,35 | - | |||||
| 0,80 | 2,10 | 3,40 | - | |||||
| 0,85 | 2,15 | 3,45 | - | |||||
| 0,90 | 2,20 | 3,50 | - | |||||
| 0,95 | 2,25 | 3,55 | - | |||||
| 1,00 | 2,30 | 3,60 | - | |||||
| 1,05 | 2,35 | 3,65 | - | |||||
| 1,10 | 2,40 | 3,70 | - | |||||
| 1,15 | 2,45 | 3,75 | - | |||||
| 1,20 | 2,50 | 3,80 | - | |||||
| 1,25 | 2,55 | 3,90 | - |
Приложение 3
Определение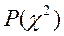
  | |||||||||||
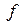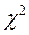| 0,6065 | 0,8013 | 0,9098 | 0,9626 | 0,9856 | 0,9948 | 0,9982 | 0,9994 | 0,9994 | 1,0 | 1,0 | |
| 0,9985 | 0,9994 | ||||||||||
| – | – | – | – | – | – |
Приложение 4
Стандартные значения критерия td для трех
степеней вероятности (по Стьюденту)
| Число степеней свободы υ | Вероятность (Р) | ||
| 0,95 | 0,99 | 0,999 | |
| 12,7 | 63,7 | 637,0 | |
| 4,3 | 9,9 | 31,6 | |
| 3,2 | 5,8 | 12,9 | |
| 2,8 | 4,6 | 8,6 | |
| 2,6 | 4,0 | 6,9 | |
| 2,4 | 3,7 | 6,0 | |
| 2,4 | 3,5 | 5,3 | |
| 2,3 | 3,4 | 5,0 | |
| 2,3 | 3,3 | 4,8 | |
| 2,2 | 3,2 | 4,6 | |
| 2,2 | 3,1 | 4,4 | |
| 2,2 | 3,1 | 4,3 | |
| 2,2 | 3,0 | 4,1 | |
| 14-15 | 2,1 | 3,0 | 4,1 |
| 16-17 | 2,1 | 2,9 | 4,0 |
| 18-20 | 2,1 | 2,9 | 3,9 |
| 21-24 | 2,1 | 2,8 | 3,8 |
| 25-28 | 2,1 | 2,8 | 3,7 |
| 29-30 | 2,0 | 2,8 | 3,7 |
| 31-34 | 2,0 | 2,7 | 3,7 |
| 35-42 | 2,0 | 2,7 | 3,5 |
| 43-62 | 2,0 | 2,7 | 3,5 |
| 63-175 | 2,0 | 2,6 | 3,4 |
| 176 и более | 2,0 | 2,6 | 3,3 |
Приложение 5
Стандартные значения критерия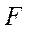 
для уровня вергоятности 0,95 (критерий Фишера)
| Число степеней свободы f2 для меньшей дисперсии | Число степеней свободы f1 для большей дисперсии, которая берется числителем | ||||||||||||
| 18,5 | 19,2 | 19,2 | 19,3 | 19,3 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,4 | 19,5 | 19,5 | |
| 10,1 | 9,6 | 9,3 | 9,1 | 9,0 | 8,9 | 8,9 | 8,8 | 8,8 | 8,8 | 8,7 | 8,6 | 8,5 | |
| 7,7 | 6,9 | 6,6 | 6,4 | 6,3 | 6,2 | 6,1 | 6,0 | 6,0 | 6,0 | 5,9 | 5,8 | 5,6 | |
| 6,6 | 5,8 | 5,4 | 5,2 | 5,1 | 5,0 | 4,9 | 4,8 | 4,8 | 4,7 | 4,7 | 4,5 | 4,4 | |
| 6,0 | 5,1 | 4,8 | 4,5 | 4,4 | 4,3 | 4,2 | 4,2 | 4,1 | 4,1 | 4,0 | 3,8 | 3,7 | |
| 5,6 | 4,7 | 4,4 | 4,1 | 4,0 | 3,9 | 3,8 | 3,7 | 3,7 | 3,6 | 3,6 | 3,4 | 3,2 | |
| 5,3 | 4,5 | 4,1 | 3,8 | 3,7 | 3,6 | 3,5 | 3,4 | 3,4 | 3,3 | 3,3 | 3,1 | 2,9 | |
| 5,1 | 4,3 | 3,9 | 3,6 | 3,5 | 3,4 | 3,3 | 3,2 | 3,2 | 3,1 | 3,1 | 2,9 | 2,7 | |
| 5,0 | 4,1 | 3,7 | 3,5 | 3,3 | 3,2 | 3,1 | 3,1 | 3,0 | 3,0 | 2,9 | 2,7 | 2,5 | |
| 4,8 | 4,0 | 3,6 | 3,4 | 3,2 | 3,1 | 3,0 | 3,0 | 2,9 | 2,9 | 2,8 | 2,6 | 2,4 | |
| 4,8 | 3,9 | 3,5 | 3,3 | 3,1 | 3,0 | 2,9 | 2,8 | 2,8 | 2,8 | 2,7 | 2,5 | 2,3 | |
| 4,7 | 3,8 | 3,4 | 3,2 | 3,0 | 2,9 | 2,8 | 2,8 | 2,7 | 2,7 | 2,6 | 2,4 | 2,2 | |
| 4,6 | 3,7 | 3,3 | 3,1 | 3,0 | 2,9 | 2,8 | 2,7 | 2,6 | 2,6 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,7 | 3,3 | 3,1 | 2,9 | 2,8 | 2,7 | 2,6 | 2,6 | 2,6 | 2,5 | 2,3 | 2,1 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,9 | 2,7 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,2 | 2,0 | |
| 4,5 | 3,6 | 3,2 | 3,0 | 2,8 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,4 | 2,2 | 2,0 | |
| 4,4 | 3,6 | 3,2 | 2,9 | 2,8 | 2,7 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,1 | 1,9 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,1 | 1,9 | |
| 4,4 | 3,5 | 3,1 | 2,9 | 2,7 | 2,6 | 2,5 | 2,4 | 2,4 | 2,4 | 2,3 | 2,1 | 1,8 | |
| 4,3 | 3,4 | 3,1 | 2,8 | 2,7 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,2 | 2,0 | 1,8 | |
| 4,3 | 3,4 | 3,0 | 2,8 | 2,6 | 2,5 | 2,4 | 2,4 | 2,3 | 2,3 | 2,2 | 2,0 | 1,7 |