Способы нахождения центра тяжести
Симметричные тела. Если тело имеет плоскость (ось, центр) симметрии, то его центр тяжести находится в этой плоскости (на оси, в центре).
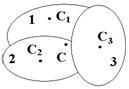 Метод разбиения. Если тело составлено из нескольких, например, трех, частей, для каждой из которых известен вес
Метод разбиения. Если тело составлено из нескольких, например, трех, частей, для каждой из которых известен вес 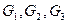 и положение центра тяжести
и положение центра тяжести 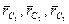 (рис. 13). Радиус-вектор центра тяжести тела
(рис. 13). Радиус-вектор центра тяжести тела 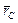 и его координаты находят по формулам:
и его координаты находят по формулам:
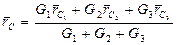 ,
, 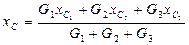 ,
,
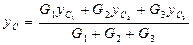 ,
, 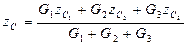 , (28)
, (28)
Метод отрицательных масс. Пусть надо найти центр тяжести нового тела, составленного из частей 1 и 2 (рис. 13). Его можно получить, вырезав из основного тела часть 3. Решение можно получить либо из (28), либо по формулам:
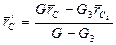 ,
, 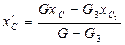 ,
,
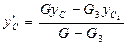 ,
, 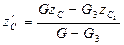 , (29)
, (29)
где 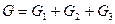 – вес основного тела.
– вес основного тела.
Распределенные силы
В статике рассматривают силы, приложенные к твердому телу в какой-либо его точке, и поэтому такие силы называют сосредоточенными. В действительности обычно силы бывают приложены к какой-либо части объема тела или его поверхности, а иногда к некоторой части линии. Так как все аксиомы и теоремы статики формулируются для сосредоточенных сил, приложенных к твердому телу, то необходимо рассмотреть способы перехода от распределенных сил к сосредоточенным в простейших, наиболее часто возникающих случаях.
 Распределенные силы прежде всего характеризуются интенсивностью распределенной силы, т.е. силой, приходящейся на единицу объема, поверхности или длины линии.
Распределенные силы прежде всего характеризуются интенсивностью распределенной силы, т.е. силой, приходящейся на единицу объема, поверхности или длины линии.
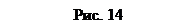 Параллельные силы постоянной интенсивности, распределенные по отрезку прямой линии. Пусть на участке
Параллельные силы постоянной интенсивности, распределенные по отрезку прямой линии. Пусть на участке 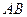 прямой линии длиной
прямой линии длиной 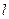 распределены параллельные силы, интенсивность которых
распределены параллельные силы, интенсивность которых 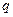 постоянна (рис. 14).
постоянна (рис. 14).
Равнодействующая сила равна 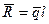 , параллельна распределенным силам и приложена вследствие симметрии распределения сил в середине отрезка
, параллельна распределенным силам и приложена вследствие симметрии распределения сил в середине отрезка 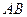 .
.
Параллельные силы, распределенные по отрезку прямой с интенсивностью, изменяющейся по линейному закону. Рассмотрим распределенные параллельные силы, изменяющиеся по линейному закону (рис. 15). Обычно считают, что такие силы распределены по треугольнику. Параллельные распределенные по треугольнику силы приводятся к равнодействующей 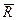 , по модулю равной
, по модулю равной 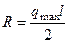 , где
, где 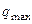 – наибольшая интенсивность силы. Точка приложения
– наибольшая интенсивность силы. Точка приложения 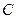 равнодействующей силы смещается в сторону, где интенсивность силы больше, и совпадает с центром тяжести площади треугольника, который находится в точке пересечения медиан, расположенной на расстоянии
равнодействующей силы смещается в сторону, где интенсивность силы больше, и совпадает с центром тяжести площади треугольника, который находится в точке пересечения медиан, расположенной на расстоянии 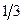 от основания треугольника и
от основания треугольника и 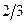 от его вершины
от его вершины 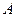 , т.е.
, т.е. 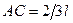 .
.
Трение
Трение скольжения
При движении или стремлении двигать одно тело по поверхности другого в касательной плоскости поверхностей соприкосновения возникает сила трения скольжения (трение первого рода).
Пусть на тело действует плоская система активных сил и тело находится в равновесии, соприкасаясь с шероховатой поверхностью другого тела (рис. 16).
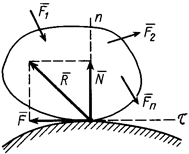 Сила реакции
Сила реакции 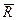 шероховатой поверхности будет складываться из нормального давления
шероховатой поверхности будет складываться из нормального давления 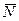 , направленного по общей нормали к поверхности соприкосновения, и силы трения скольжения
, направленного по общей нормали к поверхности соприкосновения, и силы трения скольжения 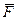 при покое.
при покое.
Для силы трения скольжения справедливы законы Кулона:
1. 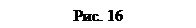 Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т.е.
Сила трения скольжения находится в общей касательной плоскости соприкасающихся поверхностей тел и направлена в сторону, противоположную направлению возможного или реального скольжения тела под действием приложенных сил. Сила трения при покое зависит от активных сил и ее модуль заключен между нулем и максимальным значением, которое достигается в момент выхода тела из положения равновесия, т.е.
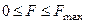 .
.
2. Максимальная сила трения скольжения при прочих равных условиях не зависит от площади соприкосновения трущихся поверхностей. Из этого закона следует, что для того, чтобы сдвинуть, например, кирпич, надо приложить одну и ту же силу независимо от того, какой гранью он положен на поверхность, широкой или узкой.
3. Максимальная сила трения скольжения пропорциональна нормальному давлению (нормальной реакции), т. е.
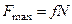 , (30)
, (30)
где безразмерный коэффициент 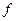 называют коэффициентом трения скольжения; он не зависит от нормального давления.
называют коэффициентом трения скольжения; он не зависит от нормального давления.
Коэффициент трения скольжения зависит от материала и физического состояния трущихся поверхностей, т.е. от величины и характера шероховатости, влажности, температуры и других условий. Коэффициент трения скольжения в зависимости от различных условий устанавливается экспериментально.
Трение качения
Если одно тело, например цилиндрический каток, катить или стремиться катить по поверхности другого тела, то кроме силы трения скольжения из-за деформации поверхностей тел дополнительно возникает пара сил, препятствующая качению катка. Явление возникновения пары сил, препятствующей качению, называют трением качения или трением второго рода.
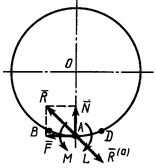
 Активные силы, действующие на катки в виде колес (рис. 17), кроме силы тяжести
Активные силы, действующие на катки в виде колес (рис. 17), кроме силы тяжести 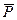 обычно состоят из силы
обычно состоят из силы 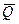 , приложенной к центру колеса параллельно общей касательной в точке
, приложенной к центру колеса параллельно общей касательной в точке 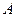 , и пары сил с моментом
, и пары сил с моментом 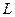 , стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если
, стремящейся катить колесо, называемое в этом случае ведомо-ведущим. Если 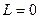 , а
, а 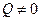 , то колесо называют ведомым; если
, то колесо называют ведомым; если 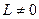 , а
, а 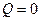 , то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
, то ведущим. Ведомо-ведущими являются колеса локомотива, идущего вторым в составе поезда.
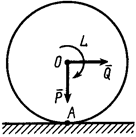
Приведем активные силы в общем случае к точке 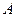 . В этой точке получим главный вектор этих сил
. В этой точке получим главный вектор этих сил 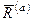 и пару сил, момент которой равен главному моменту
и пару сил, момент которой равен главному моменту 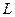 (рис. 18).
(рис. 18).
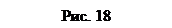 При равновесии катка, т.е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
При равновесии катка, т.е. когда каток не катится и не скользит по плоскости, активные силы уравновешиваются силами реакций связи и, следовательно,
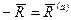 ;
; 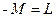 .
.
Изменив активные силы, приложенные к катку так, чтобы увеличивался момент 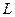 пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент
пары активных сил, стремящейся катить каток. Пока каток находится в равновесии, увеличивается и равный ему по числовой величине, но противоположный по направлению момент 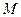 пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение
пары сил, препятствующий качению катка и возникающий от действия на каток неподвижной плоскости. Наибольшее значение 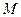 достигается в момент начала качения катка по плоскости.
достигается в момент начала качения катка по плоскости.
Установлены следующие приближенные законы для наибольшего момента пары сил, препятствующей качению:
1. Наибольший момент пары сил, препятствующей качению, в довольно широких пределах не зависит от радиуса катка.
2. Предельное значение момента 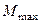 пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции
пропорционально нормальному давлению, а следовательно, и равной ему нормальной реакции 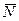 :
:
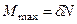 . (31)
. (31)
Коэффициент пропорциональности 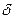 называют, коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (31) следует, что
называют, коэффициентом трения качения при покое или коэффициентом трения второго рода. Из формулы (31) следует, что 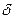 имеет размерность длины.
имеет размерность длины.
3. Коэффициент трения качения 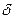 зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.
зависит от материала катка, плоскости и физического состояния их поверхностей. Коэффициент трения качения при качении в первом приближении можно считать не зависящим от угловой скорости качения катка и его скорости скольжения по плоскости.
Решение задач статики
Пример 1.На угольник 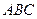 (
( 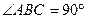 ), конец
), конец 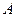 которого жестко заделан, в точке
которого жестко заделан, в точке 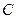 опирается стержень
опирается стержень 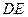 (рис. 19,а). Стержень имеет в точке
(рис. 19,а). Стержень имеет в точке 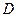 неподвижную шарнирную опору и к нему приложена сила
неподвижную шарнирную опору и к нему приложена сила 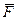 , а к угольнику – равномерно распределенная на участке
, а к угольнику – равномерно распределенная на участке 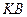 нагрузка интенсивности
нагрузка интенсивности 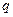 и пара с моментом
и пара с моментом 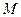 .
.
Дано: 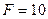 кН,
кН, 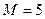
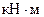 ,
, 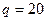
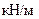 ,
, 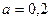 м.
м.
Определить: реакции в точках 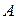 ,
, 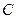 ,
, 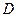 .
.
Решение:
1. Для определения реакций расчленим систему и рассмотрим сначала равновесие стержня 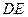 (рис. 19,б). Проведем координатные оси
(рис. 19,б). Проведем координатные оси 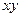 и изобразим действующие на стержень силы: силу
и изобразим действующие на стержень силы: силу 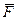 , реакцию
, реакцию 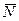 , направленную перпендикулярно стержню, и составляющие
, направленную перпендикулярно стержню, и составляющие 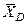 и
и 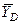 реакции шарнира
реакции шарнира 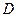 . Для полученной плоской системы сил составляем три уравнения равновесия:
. Для полученной плоской системы сил составляем три уравнения равновесия:
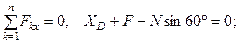 (32)
(32)
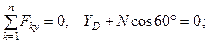 (33)
(33)
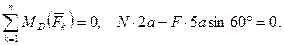 (34)
(34)
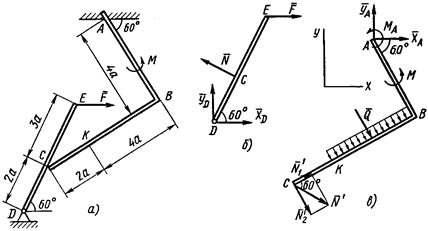
Рис. 19
2. Теперь рассмотрим равновесие угольника (рис. 19,в). На него действуют сила давления стержня 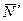 , направленная противоположно реакции
, направленная противоположно реакции 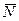 , равномерно распределенная нагрузка, которую заменяем силой
, равномерно распределенная нагрузка, которую заменяем силой 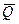 , приложенной в середине участка
, приложенной в середине участка 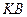 (численно
(численно 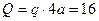 кН), пара сил с моментом
кН), пара сил с моментом 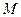 и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими
и реакция жесткой заделки, слагающаяся из силы, которую представим составляющими 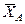 и
и 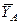 , и пары с моментом
, и пары с моментом 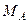 . Для этой плоской системы сил тоже составляем три уравнения равновесия:
. Для этой плоской системы сил тоже составляем три уравнения равновесия:
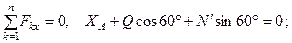 (35)
(35)
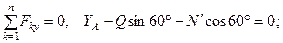 (36)
(36)
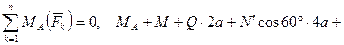
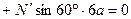 . (37)
. (37)
При вычислении момента силы 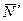 разлагаем ее на составляющие
разлагаем ее на составляющие 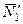 и
и 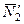 и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (32)–(37), найдем искомые реакции. При решении учитываем, что численно
и применяем теорему Вариньона. Подставив в составленные уравнения числовые значения заданных величин и решив систему уравнений (32)–(37), найдем искомые реакции. При решении учитываем, что численно 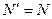 в силу равенства действия и противодействия.
в силу равенства действия и противодействия.
Ответ: 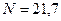 кН,
кН, 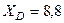 кН,
кН, 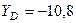 кН,
кН, 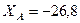 кН,
кН, 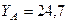 кН,
кН, 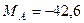
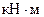 . Знаки минус указывают, что силы
. Знаки минус указывают, что силы 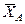 ,
, 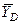 и момент
и момент 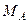 направлены противоположно показанным на рис. 19.
направлены противоположно показанным на рис. 19.
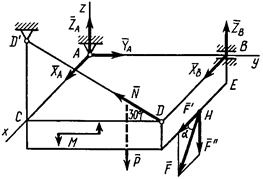
Пример 2.Горизонтальная прямоугольная плита весом 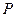 (рис. 20) закреплена сферическим шарниром в точке
(рис. 20) закреплена сферическим шарниром в точке 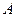 , цилиндрическим (подшипником) в точке
, цилиндрическим (подшипником) в точке 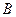 и невесомым стержнем
и невесомым стержнем 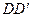 . На плиту в плоскости, параллельной
. На плиту в плоскости, параллельной 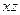 , действует сила
, действует сила 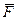 , а в плоскости, параллельной
, а в плоскости, параллельной 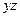 , – пара сил с моментом
, – пара сил с моментом 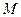 .
.
 Дано:
Дано: 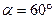 ,
, 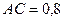 м,
м, 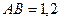 м,
м, 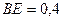 м,
м, 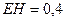 м,
м, 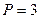 кН,
кН, 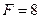 кН,
кН, 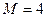
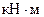 .
.
Определить: реакции опор 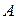 ,
, 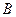 и стержня
и стержня 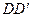 .
.
 Решение:
Решение:
1. Рассмотрим равновесие плиты. На плиту действуют заданные силы 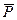 ,
, 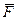 и пара с моментом
и пара с моментом 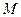 , а также реакции связей. Реакцию сферического шарнира разложим на три составляющие
, а также реакции связей. Реакцию сферического шарнира разложим на три составляющие 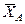 ,
, 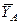 и
и 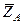 , цилиндрического (подшипника) – на две составляющие
, цилиндрического (подшипника) – на две составляющие 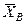 и
и 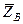 (в плоскости, перпендикулярной оси подшипника); реакцию
(в плоскости, перпендикулярной оси подшипника); реакцию 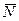 стержня направляем вдоль стержня от
стержня направляем вдоль стержня от 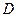 к
к 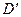 , предполагая, что он растянут.
, предполагая, что он растянут.
2. Для определения шести неизвестных реакций составляем шесть уравнений равновесия действующей на плиту пространственной системы сил:
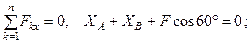 (38)
(38)
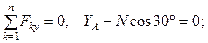 (39)
(39)
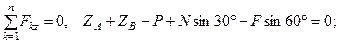 (40)
(40)
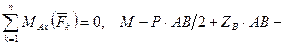
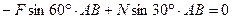 ; (41)
; (41)
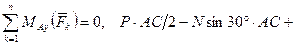
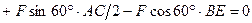 ; (42)
; (42)
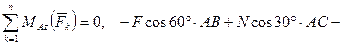
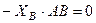 . (43)
. (43)
Для определения моментов силы 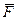 относительно осей
относительно осей 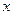 и
и 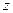 разлагаем ее на составляющие
разлагаем ее на составляющие 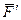 и
и 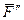 , параллельные осям
, параллельные осям 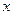 и
и 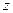 (
( 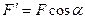 ,
, 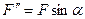 ), и применяем теорему Вариньона.
), и применяем теорему Вариньона.
Аналогично можно поступить при определении моментов реакции 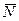 .
.
Подставив в составленные уравнения числовые значения всех заданных величин и решив эти уравнения, найдем искомые реакции.
Ответ: 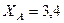 кН,
кН, 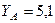 кН,
кН, 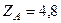 кН,
кН, 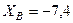 кН,
кН, 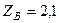 кН,
кН, 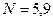 кН. Знак минус указывает, что реакция
кН. Знак минус указывает, что реакция 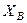 направлена противоположно показанной на рис. 20.
направлена противоположно показанной на рис. 20.
ЛЕКЦИЯ № 3
КИНЕМАТИКА
Кинематика точки
В кинематике точки рассматриваются характеристики движения точки, такие, как скорость, ускорение, и методы их определения при различных способах задания движения. Важным в кинематике точки является понятие траектории. Траекторией точки называется геометрическое место ее последовательных положений в пространстве с течением времени относительно рассматриваемой системы отсчета. По виду траекторий движения точки делятся на прямолинейные и криволинейные.
Задать движение точки – значит задать правило, с помощью которого можно указать положение точки в любой момент времени. Существуют векторный, координатный и естественный способы задания движения точки.
Скорость и ускорение точки
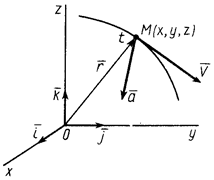
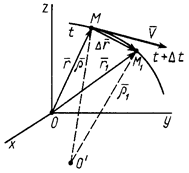 Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 21).
Одной из основных характеристик движения точки является ее скорость относительно выбранной системы отсчета, которая изображена в виде декартовой прямоугольной системы координат (рис. 21).
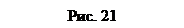 Положение движущейся точки
Положение движущейся точки 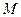 относительно рассматриваемой системы отсчета определяется в момент времени
относительно рассматриваемой системы отсчета определяется в момент времени 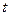 радиусом-вектором
радиусом-вектором  , который соединяет неподвижную точку
, который соединяет неподвижную точку 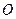 с этой точкой. В другой момент времени
с этой точкой. В другой момент времени 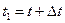 движущаяся точка займет положение
движущаяся точка займет положение 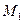 и ее радиусом-вектором будет
и ее радиусом-вектором будет 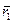 . За время
. За время 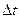 радиус-вектор движущейся точки изменится на
радиус-вектор движущейся точки изменится на 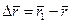 .
.
Средней скоростью 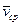 точки за время
точки за время 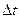 называют отношение
называют отношение 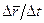 , т.е.:
, т.е.:
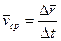 .
.
Средняя скорость параллельна вектору 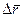 . В общем случае она зависит от времени осреднения
. В общем случае она зависит от времени осреднения 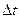 . У нее нет конкретной точки приложения на траектории.
. У нее нет конкретной точки приложения на траектории.
Введем скорость точки 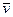 в момент
в момент 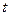 , которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.
, которая определяется как предел средней скорости, если промежуток времени, за который определяется средняя скорость, стремится к нулю, т. е.
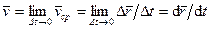 .
.
Скорость точки направлена в сторону ее движения по предельному направлению вектора 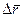 при
при 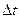 , стремящемся к нулю, т.е. по предельному направлению секущей
, стремящемся к нулю, т.е. по предельному направлению секущей 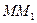 , которая совпадает с касательной к траектории в точке
, которая совпадает с касательной к траектории в точке 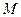 . Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.
. Таким образом, скорость точки равна первой производной по времени от ее радиуса-вектора. Она направлена по касательной к траектории в сторону движения точки.
Начало радиуса-вектора движущейся точки можно выбрать в любой неподвижной точке. На рис. 21 представлен случай, в котором радиусом-вектором является также 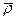 с началом в точке
с началом в точке 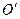 . Радиусы-векторы имеют одинаковые изменения
. Радиусы-векторы имеют одинаковые изменения 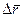 и
и 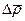 за время
за время 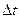 и поэтому
и поэтому
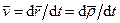 . (44)
. (44)
Пусть движущаяся точка 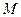 в момент времени
в момент времени 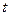 имеет скорость
имеет скорость 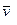 . В момент времени
. В момент времени 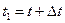 эта точка занимает положение
эта точка занимает положение 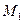 , имея скорость
, имея скорость 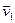 (рис. 22). Чтобы изобразить приращение скорости
(рис. 22). Чтобы изобразить приращение скорости 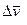 за время
за время 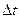 , перенесем вектор скорости
, перенесем вектор скорости 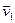 параллельно самому себе в точку
параллельно самому себе в точку 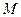 .
.
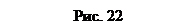
 Средним ускорением точки
Средним ускорением точки 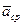 за время
за время 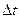 называют отношение
называют отношение 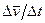 , т.е.
, т.е. 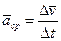 . Среднее ускорение точки параллельно приращению скорости
. Среднее ускорение точки параллельно приращению скорости 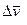 . Как и средняя скорость, среднее ускорение не имеет на траектории конкретной
. Как и средняя скорость, среднее ускорение не имеет на траектории конкретной  течки приложения и изображено в точке
течки приложения и изображено в точке 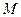 условно. В общем случае среднее ускорение зависит от времени
условно. В общем случае среднее ускорение зависит от времени 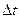 .
.
Ускорением точки 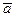 в момент времени
в момент времени 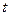 называют предел, к которому стремится среднее ускорение при
называют предел, к которому стремится среднее ускорение при 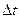 , стремящемся к нулю, т. е.
, стремящемся к нулю, т. е.
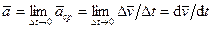 . (45)
. (45)
Таким образом, ускорение точки равно первой производной по времени от скорости точки.
Приращение скорости 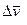 и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при
и, следовательно, среднее ускорение направлены внутрь вогнутости траектории. Так же направлены и их предельные значения при 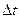 , стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории.
, стремящемся к нулю. Поэтому ускорение точки направлено тоже внутрь вогнутости траектории.
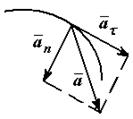 Ускорение точки можно представить в виде (рис. 23):
Ускорение точки можно представить в виде (рис. 23):
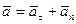 . (46)
. (46)
Часть ускорения, равная
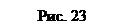
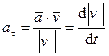 ,
,
называется касательной составляющей ускорения. Она направлена по касательной к траектории. Другая часть ускорения
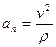
называется нормальной составляющей ускорения (  – радиус кривизны траектории). Она направлена внутрь вогнутости траектории, перпендикулярно
– радиус кривизны траектории). Она направлена внутрь вогнутости траектории, перпендикулярно 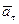 .
.
 2.1.2. Векторный способ задания движения точки
2.1.2. Векторный способ задания движения точки
 Движение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиусом-вектором
Движение точки относительно рассматриваемой системы отсчета при векторном способе изучения движения задается радиусом-вектором  этой точки (рис. 24). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.
этой точки (рис. 24). Движение точки считается заданным, если известен радиус-вектор движущейся точки как функция времени, т. е.
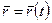 . (47)
. (47)
Задание векторного уравнения движения (47) полностью определяет движение точки.
Скорость точки направлена по касательной к траектории и вычисляется, согласно ее определению, по формуле:
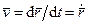 . (48)
. (48)
Для ускорения точки соответственно имеем
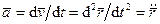 . (49)
. (49)
Определение скорости и ускорения точки сводится к чисто математической задаче вычисления первой и второй производных по времени от радиуса-вектора этой точки.
2.1.3. Координатный способ задания движения точки
Движение точки в декартовых координатах считается заданным, если известны координаты точки как непрерывные, дважды дифференцируемые функции времени (рис. 24), т. е. заданы уравнения движения точки в декартовых координатах:
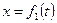 ,
,  ,
, 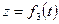 . (50)
. (50)
Уравнения движения точки в декартовых координатах полностью определяют движение точки. Они позволяют найти положение точки, ее скорость и ускорение в любой момент времени.
Разложим радиус-вектор и скорость точки на составляющие, параллельные осям координат. Получим
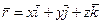 ,
, 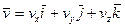 , (51)
, (51)
где  – координаты точки
– координаты точки 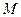 ;
; 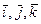 – единичные векторы осей координат;
– единичные векторы осей координат; 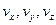 – проекции скорости на оси координат.
– проекции скорости на оси координат.
Учитывая (51), согласно определению скорости, имеем:
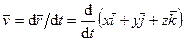
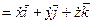 , (52)
, (52)
Сравнивая (52) и (51), получаем для проекций скорости на декартовы оси координат следующие формулы:
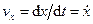 ,
, 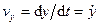 ,
, 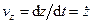 . (53)
. (53)
Проекция скорости точки на какую-либо координатную ось равна первой производной по времени от соответствующей координаты этой точки. По проекциям определяют числовое значение (модуль) скорости и косинусы углов вектора скорости с осями координат:
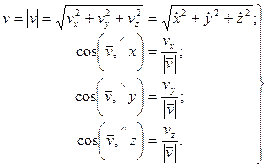 (54)
(54)
Разложим ускорение точки на составляющие, параллельные осям декартовой системы координат. Получим
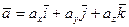 , (55)
, (55)
где 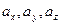 – проекции ускорения на координатные оси. Согласно определению ускорения и формулам (52) и (51), имеем
– проекции ускорения на координатные оси. Согласно определению ускорения и формулам (52) и (51), имеем
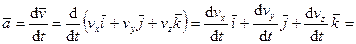
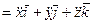 . (56)
. (56)
Формулы для проекций ускорения на оси декартовой системы координат:
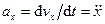 ,
, 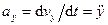 ,
, 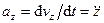 . (57)
. (57)
Проекция ускорения на какую-либо координатную ось равна второй производной по времени от соответствующей координаты движущейся точки.
Числовое значение ускорения и косинусы углов вектора ускорения с осями координат определяем по формулам
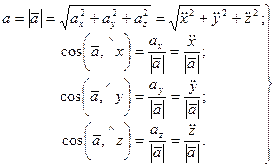 . (58)
. (58)
Касательная и нормальная составляющие ускорения вычисляются по формулам:
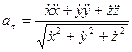 ,
, 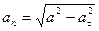 . (59)
. (59)
При 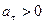 движение точки ускоренное, при
движение точки ускоренное, при 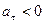 – замедленное.
– замедленное.
2.1.4. Естественный способ задания движения точки
 При естественном способе задания движения задаются траектория и закон движения точки по траектории. Движение точки рассматривается относительно фиксированной системы
При естественном способе задания движения задаются траектория и закон движения точки по траектории. Движение точки рассматривается относительно фиксированной системы 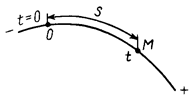 отсчета.
отсчета.
Для задания закона движения точки по траектории необходимо выбрать на траектории точку 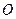 , принимаемую за начало отсчета расстояний (рис. 25). Расстояния в одну сторону от точки
, принимаемую за начало отсчета расстояний (рис. 25). Расстояния в одну сторону от точки 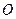 по траектории считаются положительными (например, вправо), в другую – отрицательными. Кроме того, следует задать начало отсчета времени. Обычно за
по траектории считаются положительными (например, вправо), в другую – отрицательными. Кроме того, следует задать начало отсчета времени. Обычно за 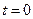 принимают момент времени, в который движущаяся точка проходит через точку
принимают момент времени, в который движущаяся точка проходит через точку 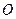 , или момент начала движения. Время до этого события считается отрицательным, а после него – положительным.
, или момент начала движения. Время до этого события считается отрицательным, а после него – положительным.
Если в момент времени 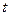 движущаяся точка занимает положение
движущаяся точка занимает положение 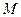 , то закон движения точки по траектории задается зависимостью от времени расстояния
, то закон движения точки по траектории задается зависимостью от времени расстояния 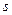 , отсчитываемого от точки
, отсчитываемого от точки 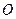 до точки
до точки 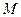 , т. е.
, т. е. 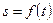 . Эта функция должна быть непрерывной и дважды дифференцируемой.
. Эта функция должна быть непрерывной и дважды дифференцируемой.
При естественном способе задания движения используется понятие естественных осей координат. Сначала в точке строится соприкасающаяся окружность, которая наиболее плотно смыкается с траекторией из всех возможных. Ее центр называют центром кривизны траектории. Плоскость, в которой лежит соприкасающаяся окружность, называется соприкасающейся плоскостью.
Построим в точке 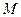 кривой линии естественные оси этой кривой (рис. 26). Первой естественной осью является касательная
кривой линии естественные оси этой кривой (рис. 26). Первой естественной осью является касательная 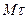 . Ее положительное направление совпадает с направлением единичного вектора касательной
. Ее положительное направление совпадает с направлением единичного вектора касательной 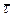 , направленного в сторону возрастающих расстояний.
, направленного в сторону возрастающих расстояний.
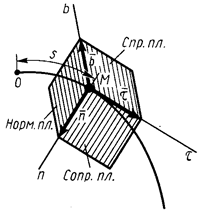 Перпендикулярно касательной
Перпендикулярно касательной 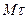 располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью
располагается нормальная плоскость кривой. Нормаль, расположенная в соприкасающейся плоскости, называется главной нормалью 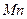 . Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью.
. Она является линией пересечения нормальной плоскости с соприкасающейся плоскостью.
По главной нормали внутрь вогнутости кривой направим единичный вектор 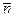 . Он определяет положительное направление второй естественной оси.
. Он определяет положительное направление второй естественной оси.
Нормаль, перпендикулярная главной нормали, называется бинормалью. Единичный вектор 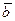 , направленный по бинормали так, чтобы три вектора
, направленный по бинормали так, чтобы три вектора 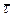 ,
, 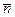 и
и 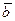 образовывали правую систему осей координат, определит положительное направление третьей естественной оси.
образовывали правую систему осей координат, определит положительное направление третьей естественной оси.
Три взаимно перпендикулярные оси 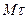 ,
, 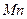 и
и 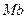 , положительные направления которых совпадают с направлениями единичных векторов
, положительные направления которых совпадают с направлениями единичных векторов 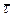 ,
, 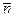 и
и 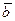 , называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
, называются естественными осями кривой. Эти оси образуют в точке М естественный трехгранник. При движении точки по кривой естественный трехгранник движется вместе с точкой как твердое тело, поворачиваясь вокруг вершины, совпадающей с движущейся точкой.
Используя определение скорости, имеем:
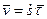 ,
,
где 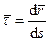 . Вектор
. Вектор 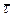 направлен по касательной к траектории как производная от вектора по скалярному аргументу и является единичным вектором. Модуль этого вектора равен единице, как предел отношения длины хорды
направлен по касательной к траектории как производная от вектора по скалярному аргументу и является единичным вектором. Модуль этого вектора равен единице, как предел отношения длины хорды 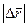 к длине стягивающей ее дуги
к длине стягивающей ее дуги 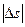 при стремлении ее к нулю.
при стремлении ее к нулю.
Единичный вектор 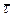 всегда направлен по касательной к траектории в сторону возрастающих (положительных) расстояний независимо от направления движения точки.
всегда направлен по касательной к траектории в сторону возрастающих (положительных) расстояний независимо от направления движения точки.
Величина 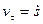 называется алгебраической скоростью точки. Ее можно считать проекцией скорости на положительное направление касательной к траектории, совпадающее с направлением единичного вектора
называется алгебраической скоростью точки. Ее можно считать проекцией скорости на положительное направление касательной к траектории, совпадающее с направлением единичного вектора 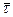 .
.
Естественное задание движения точки полностью определяет скорость точки по величине и направлению. Алгебраическую скорость находят дифференцированием по времени закона изменения расстояний. Единичный вектор 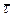 определяют по заданной траектории.
определяют по заданной траектории.
В соответствии с определением ускорения получаем
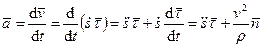 , (60)
, (60)
так как 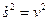 и
и 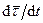 направлен внутрь вогнутости траектории параллельно единичному вектору главной нормали
направлен внутрь вогнутости траектории параллельно единичному вектору главной нормали 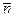 .
.
Получено разложение ускорения точки по осям естественного трехгранника. Касательная, нормальная составляющие и полное ускорение равны
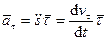 ,
, 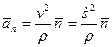 ,
, 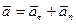 . (61)
. (61)
