Средние показатели рядов динамики

Средние – обобщающие характеристики динамического ряда и скорости и интенсивности изменения уровней ряда.

Средний уровень ряда

Для интервальных динамических рядов средний уровень ряда рассчитываются на основе средней арифметической простой:

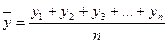, где n – число уровней ряда.

Для моментных рядов средний уровень ряда рассчитывается на основе средней хронологической:

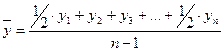
Средний абсолютный прирост

Рассчитывается на основе цепных абсолютных приростов и характеризует на сколько в среднем в единицу времени изменялись уровни изучаемого ряда.

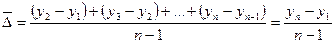
Средний темп роста

Рассчитывается по средней геометрической

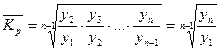
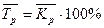
Средний темп прироста

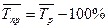
На сколько процентов в среднем в единицу времени изменялись уровни изучаемого временного ряда.

При комментарии полученных значений средних показателей обязательно следует указывать на период времени, который описывается динамическим рядом, а также на период времени, к которому относится уровень изучаемого ряда.

36. Компоненты временного ряда.

Уровни временных рядов формируются под влиянием множества факторов. Одни из них действуют стабильно на протяжении длительного периода времени и формируют основную тенденцию временного ряда, которую называют трендом (T). Другие факторы (ряд факторов) влияют на уровни ряда с определенной периодичностью. Их действия называют циклическими (C).

Для изучения влияния циклических факторов необходимы достаточно длинные временные ряды.

Сезонные факторы (S). Влияние этих факторов может быть изучено, когда уровни ряда представлены внутригодичными данными (то есть показателями, характеризующими либо квартал, либо месяц).

Случайные факторы (E). Действуют без определенной периодичности. Практически не поддаются изучению.

Исходя из вышесказанного, уровень ряда может быть представлен как функция четырех компонент:

y = f (T, S, C, E)

Чем сильнее влияние нетрендовых компонент (S, C, E), тем сложнее выявить и описать основную тенденцию ряда (тренд), что является основной задачей изучения временных рядов.

37. Сглаживание рядов динамики: механическое, аналитическое.

Существует два метода выравнивания:

• механическое;
• аналитическое.

Любое выравнивание предполагает замену фактических уровней изучаемого ряда на теоретические, полученные в результате определенных расчетов и в той или иной мере очищенные от влияния случайных колебаний.

Механическое выравнивание осуществляется двумя способами:

ü укрупнение интервалов

ü метод скользящей средней

Пример: имеются данные о выпуске продукции на предприятии по месяцам.

месяц
Выпуск продукции (млн. руб.)	5,1	5,4	5,2	5,3	5,6	5,8	5,6	5,9	6,1	6,0	5,9	6,2

1) Метод укрупнения интервалов предполагает объединение временных периодов и расчет по ним либо суммарных значений показателей, либо средних величин.

Результат укрупнения интервалов будет выглядеть:

квартал	Выпуск продукции (млн. руб)
в абсолютном выражении	среднемесячный
I	15,7	5,2
II	16,7	5,6
III	17,6	5,9
IV	18,1	6,0

2) Метод скользящей средней.

Предполагает расчеты среднего уровня за определенный временной интервал и дальнейшее продвижение интервала на один шаг.

Рассчитанные средние (выровненные) уровни относятся к середине интервала, по которому рассчитываются средние

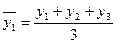
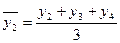
Если период скольжения – четная величина, то применяют прием центрирования.

Прием центрирования выражается в подсчете средней арифметической величины из значений, полученных по двум шагам скольжения.

Увеличение периода скольжения позволяет более отчетливо проявиться основной тенденции, однако существенно укорачивает изучаемый временной ряд, что неблагоприятно может сказаться на качестве трендовой модели.

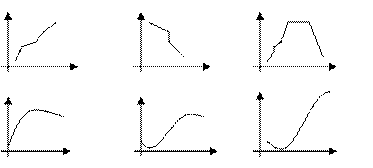
Аналитическое выравнивание позволяет не только выявить основную тенденцию ряда, но и получить аналитическую форму тренда. Уравнение тренда – это парное уравнение регрессии, в качестве фактора в котором выступает время:

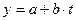, где y – уровень временного ряда

a, b – параметры уравнения тренда

t – время.

38. Понятие тренда, критерии выбора вида трендовой модели.

Расчет параметров трендовой модели осуществляется с использованием метода наименьших квадратов.

Прежде чем получить трендовую модель, нужно выбрать уравнение тренда, лучшим образом описывающее реальную тенденцию изучаемого ряда.

Выбор уравнения тренда может быть осуществлен:

1.На основе графического представления временного ряда. На графике по оси абсцисс откладываются периоды или моменты времени, по оси ординат – уровни временного ряда.

2.Теоретический анализ объекта исследования и анализ показателей изменения уровней динамического ряда. Очень часто используется метод конечных разностей. Так если примерно постоянными являются первые разности (абсолютные приросты), то можно использовать полином первой степени (линейную функцию). Если примерно постоянными являются вторые разности (ускорение), то следует использовать полином второй степени и так далее.

3.В настоящее время выбор лучшей функции для описания тренда формализован, то есть осуществляется с использованием пакетов прикладных программ на основе определенных критериев.

Поскольку основная задача построения уравнения тренда – это лучшая аппроксимация имеющихся фактических данных, то среди критериев отбора можно выделить следующие:

§ минимизация суммы квадратов отклонений фактических значений от значений, полученных в уравнении тренда

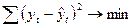, где

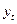- фактические уровни ряда;

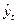- теоретические, выровненные, полученные на основе уравнения тренда уровни ряда.

§ стандартная ошибка

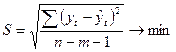, где

n – длина динамического ряда;

m – число факторов, включенных в анализ.

§ среднее линейное (абсолютное) отклонение.

Средняя ошибка аппроксимации

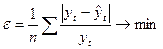
§ F-критерий Фишера → max

§ коэффициент детерминации R² → max

Основным критерием качества трендовой модели является оценка остатков трендовой модели на наличие автокорреляции. Остатки – это разность между фактическими значениями уровней временного ряда и выровненными значениями, то есть полученными по уравнению тренда.

39. Оценка качества модели динамического ряда. Критерий Дарбина-Вотсона.

Основным критерием качества трендовой модели является оценка остатков трендовой модели на наличие автокорреляции. Остатки – это разность между фактическими значениями уровней временного ряда и выровненными значениями, то есть полученными по уравнению тренда.

Автокорреляция в остатках – зависимость последующих остатков от предшествующих.

Оценка автокорреляции в остатках может быть проведена с использованием парного коэффициента корреляции или специального критерия – критерия Дарвина-Уотсона (D-W).

-

-

-

…

-

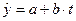
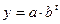
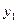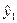
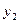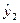
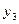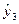
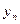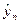
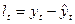- остаток;

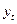- фактическое значение;

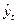- теоретическое значение.

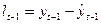- остаток периода, предшествующего периоду t.

Корреляционная зависимость между l_t и l_t-1 – автокорреляция в остатках.

Наличие автокорреляции в остатках свидетельствует о наличии тенденции в остатках. Поскольку трендовая модель должна полностью описывать основную тенденцию ряда, то сохранение тенденции в остатках говорит о том, что модель не может быть признана удовлетворительной.