Операции над событиями. Алгебра событий.
Операции над событиями. Алгебра событий.
Алгебра событий – это множество S=2^n элементов, в которых содержатся операции умножения и сложения.
А) Объединяя благоприятствующие события А и В исходы, мы получаем подмножества во множестве W, то есть событие которое называется суммой событий А и В , и обозначается: А 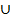 В.
В.
Б) Выбирая благоприятствующие исходы, одновременно принадлежащие и событию А, и событию В, мы получаем некоторое подмножество пустое (в случае если А и В несовместна) или непустое (А и В совместны), которое называется произведением А и В, и обозначается А 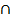 В.
В.
Дадим аксиоматическое определение вероятности любого события, входящего в алгебру S (для случая конечного n-исходов опыта). Определяем через постулаты:
1) Каждому элементарному исходу wi (i 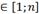 ) поставим в соответствие некоторым разумным способом положительное число Р(wi).
) поставим в соответствие некоторым разумным способом положительное число Р(wi).
2) Сумма всех положительных чисел Р(wi) , где i  , равна 1. Каждое из этих чисел называется вероятностью соответствующего исхода.
, равна 1. Каждое из этих чисел называется вероятностью соответствующего исхода.
3) Вероятность любого события, связанного с данным опытом, а значит включенного в алгебру S, равна сумме вероятностей исходов, приводящих к этому событию, то есть благоприятствующих исходов.

Аксиомы Колмогорова. Аксиоматическая теория Колмогорова основывается на пяти аксиомах, с помощью которых вводятся понятия вероятности и некоторые их свойства как для конечного множества элементарных событий, так и для любого бесконечного множества. Вот эти аксиомы:
1. Каждому событию А, принадлежащему F, ставится в соответствие неотрицательное число Р(А), которое называется вероятностью события А.
2. Вероятность достоверного события Р(F) = 1.
3. Вероятность невозможного события Р(Ø) = 0.
4. Аксиома сложения. Если  попарно не совместны, то
попарно не совместны, то 
5. Расширенная аксиома сложения. Если  попарно не совместны, то
попарно не совместны, то  (Здесь счетное множество действий).
(Здесь счетное множество действий).
Определение 3. Пространство элементарных событий Ω, σ-алгебра событий F и вероятность Р(·) на F, удовлетворяющие 5-ти аксиомам вероятности определяют вероятностное пространство, обозначаемое (Ω, F, P).
Замечание 25.
Следовало бы крикнуть «ура!»: свойство, о котором мы давно мечтали, — чтобы независимость следовала из некоррелированности, — имеет все же место. Но только для наборов случайных величин с нормальным совместным распределением, и это — очередное изумительное качество нормального распределения.
Доказательство.Только в случае диагональной матрицы  с элементами
с элементами  квадратичная форма (37) превращается в сумму квадратов
квадратичная форма (37) превращается в сумму квадратов

и многомерная плотность распадается в произведение плотностей координат.
Q.D.E.
Надеюсь, читатель поверит следующей теореме без доказательства, будучи в состоянии доказать ее, как и в одномерном случае, с помощью многомерных характеристических функций.
Следствие 5.
В условиях многомерной ЦПТ имеет место сходимость  .
.
42 корреляция
Среднеквадратичным отклонением (англ. standart deviation) 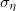 называется величина, равная квадратному корню из дисперсии случайной величины
называется величина, равная квадратному корню из дисперсии случайной величины 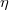
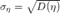
Пусть 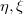 — две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда корреляцией случайных величин(англ. correlation)
— две случайные величины, определённые на одном и том же вероятностном пространстве. Тогда корреляцией случайных величин(англ. correlation) 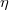 и
и 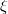 называется выражение следующего вида:
называется выражение следующего вида:
 , где
, где 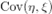 — ковариация случайных величин.
— ковариация случайных величин.
Заметим, что 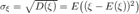 — среднеквадратичное отклонение.
— среднеквадратичное отклонение.
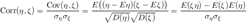
Значительная корреляция между случайными величинами всегда означает, что присутствует некая взаимосвязь между значениями конкретной выборки, но при другой выборке связь вполне может отсутствовать. Поэтому при нахождении взаимосвязи не нужно делать поспешных выводов о причинно-следственном характере величин, а следует рассмотреть наиболее полную выборку, чтобы делать какие-либо выводы. Коэффициенты корреляции устанавливают лишь статистические взаимосвязи, но не более того.
Если  , то
, то 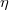 и
и 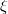 линейно зависимы.
линейно зависимы.
Если 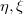 независимые случайные величины, то
независимые случайные величины, то 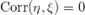 .
.
Пусть 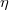 и и 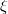 — независимые величины. Тогда — независимые величины. Тогда 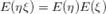 , где , где 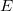 — их математическое ожидание. Получаем: — их математическое ожидание. Получаем: 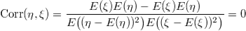 Но обратное неверно: Пусть Но обратное неверно: Пусть  — случайная величина, распределенная симметрично около — случайная величина, распределенная симметрично около  , а , а  . . 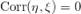 , но , но 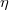 и и 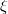 — зависимые величины. — зависимые величины. |
43. 
44. Генеральная и выборочная совокупности
Пусть требуется изучить совокупность однородных объектов относительно некоторого качественного или количественного признака, характеризующего эти объекты. Например, если имеется партия деталей, то качественным признаком может служить стандартность детали, а количественным – контролируемый размер детали.
Иногда проводят сплошное обследование, то есть обследуют каждый из объектов совокупности относительно признака, которым интересуются. На практике, однако, сплошное обследование применяют сравнительно редко. Например, если совокупность содержит очень большое число объектов, то провести сплошное обследование физически невозможно. Если обследование объекта связано с его уничтожением или требует больших материальных затрат, то проводить сплошное обследование практически не имеет смысла. В таких случаях случайно отбирают из всей совокупности ограниченное число объектов и подвергают их изучению. Различают генеральную и выборочную совокупности:
Выборочной совокупностью или просто выборкой называют совокупность случайно отобранных объектов.
Генеральной совокупностью называют совокупность объектов, из которых производится выборка.
Объемом совокупности (выборочной или генеральной) называют число объектов этой совокупности. Например, если из 1000 деталей отобрано для обследования 100 деталей, то объем генеральной совокупности 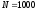 , а объем выборки
, а объем выборки 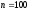 .[1]
.[1]
Замечание. Часто генеральная совокупность содержит конечное число объектов. Однако, если это число достаточно велико, то иногда в целях упрощения вычислений, или для облегчения теоретических выводом, допускают, что генеральная совокупность состоит из бесчисленного множества объектов. Такое допущение оправдывается тем, что увеличение объема генеральной совокупности (достаточно большого объема) практически не сказывается на результатах обработки данных выборки. [3]
Способы отбора
На практике применяются различные способы отбора. Принципиально эти способы можно подразделить на два вида:
Отбор, не требующий расчленения генеральной совокупности на части. Сюда относятся: а) простой случайный бесповторный отбор; б) простой случайный повторный отбор.
Отбор, при котором генеральная совокупность разбивается на части. Сюда относятся: а) типический отбор; б) механический отбор; в) серийный отбор.
Простым случайным называют такой отбор, при котором объекты извлекают по одному из всей генеральной совокупности. Осуществить простой отбор можно различными способами. Например, для извлечения  объектов из генеральной совокупности объема
объектов из генеральной совокупности объема 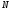 поступают так: выписывают номера от 1 до
поступают так: выписывают номера от 1 до 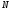 на карточках, которые тщательно перемешивают, и наугад вынимают одну карточку; объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию; затем карточку возвращают в пачку и процесс повторяют, то есть карточки перемешивают, наугад вынимают одну из них и так далее. Так поступают
на карточках, которые тщательно перемешивают, и наугад вынимают одну карточку; объект, имеющий одинаковый номер с извлеченной карточкой, подвергают обследованию; затем карточку возвращают в пачку и процесс повторяют, то есть карточки перемешивают, наугад вынимают одну из них и так далее. Так поступают  раз; в итоге получают простую случайную выборку объема
раз; в итоге получают простую случайную выборку объема  .
.
Если извлеченные карточки не возвращать в пачку, то выборка является простой случайной бесповторной.
При большом объеме генеральной совокупности описанный процесс оказывается очень трудоемким. В этом случае пользуются готовыми таблицами «случайных чисел», в которых числа расположены в случайном порядке. Для того, что отобрать, Типическим называется отбор, при котором объекты отбираются не из всей генеральной совокупности, а из каждой ее «типической» части
Механическим называют отбор, при котором генеральную совокупность «механически» делят на столько групп, сколько объектов должно войти в выборку, а из каждой группы отбирают один объект.
Серийным называют отбор, при котором объекты отбирают из генеральной совокупности не по одному, а «сериями», которые подвергаются сплошному обследованию. Подчеркнем, что на практике часто применяется комбинированный отбор, при котором сочетаются указанные выше способы.
45 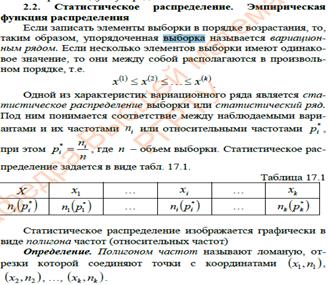


46.Статистическая оценка неизвестных параметров Всякая генеральная совокупность так же, как и любая стохастическая модель (будь то модель регрессионной зависимости, модель главных компонент, модель факторного анализа и т. д., см. ниже) характеризуется набором числовых параметров 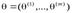 ¢. [1], в качестве таких параметров выступают компоненты вектора средних значений
¢. [1], в качестве таких параметров выступают компоненты вектора средних значений 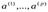 и элементы ковариационной матрицы
и элементы ковариационной матрицы 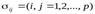 , так что в этом случае размерностьт вектора
, так что в этом случае размерностьт вектора 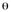
 равна, как легко подсчитать,р + р (р+ 1)/2.Однако практически чаще всего точные значения этих «определяющих» параметров неизвестны, и нам приходится судить о них лишь на основании имеющихся в нашем распоряжении результатов наблюдения (выборочных данных).а) Статистика, статистическая оценка, ее свойства. Любую функцию
равна, как легко подсчитать,р + р (р+ 1)/2.Однако практически чаще всего точные значения этих «определяющих» параметров неизвестны, и нам приходится судить о них лишь на основании имеющихся в нашем распоряжении результатов наблюдения (выборочных данных).а) Статистика, статистическая оценка, ее свойства. Любую функцию  от результатов наблюдения
от результатов наблюдения  в вероятностно-статистической литературе принято называтьстатистикой. Именно статистикиобычно используются для построения статистических оценок параметров
в вероятностно-статистической литературе принято называтьстатистикой. Именно статистикиобычно используются для построения статистических оценок параметров 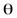 , относительная частота
, относительная частота
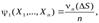 являющаяся оценкой вероятности Р (DS); выборочная плотность
являющаяся оценкой вероятности Р (DS); выборочная плотность 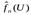 (1.4'), являющаяся оценкой теоретической плотности f(U) в точке U; выборочные средние
(1.4'), являющаяся оценкой теоретической плотности f(U) в точке U; выборочные средние 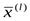 и выборочные ковариации
и выборочные ковариации 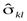 (1.6") и (1.7"), являющиеся оценками соответственно теоретических средних
(1.6") и (1.7"), являющиеся оценками соответственно теоретических средних 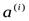 и ковариаций
и ковариаций 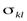 . Метод, который чаще приводит к наилучшим оценкам, называется метод максимального правдоподобия (предложен Р. Фишером).Пусть
. Метод, который чаще приводит к наилучшим оценкам, называется метод максимального правдоподобия (предложен Р. Фишером).Пусть 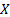 – непрерывная случайная величина, которая в результате
– непрерывная случайная величина, которая в результате 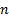 испытаний приняла значения
испытаний приняла значения 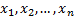 . Пусть вид плотности распределения данной случайной величины известен, но не известен параметр
. Пусть вид плотности распределения данной случайной величины известен, но не известен параметр 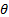 , которым определяется эта функция.
, которым определяется эта функция.
Определение 16.4. Функция вида:  называется функцией правдоподобия.
называется функцией правдоподобия.
Метод максимального правдоподобия заключается в том, что в качестве оценок параметра 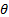 принимается то значение
принимается то значение 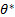 , при котором функция
, при котором функция 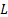 принимает максимальное значение. Экстремум функций
принимает максимальное значение. Экстремум функций 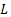 и
и 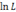 достигается при одних и тех же значениях
достигается при одних и тех же значениях 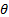 . Удобнее находить максимум функции
. Удобнее находить максимум функции 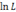 . Поэтому критические значения определяются из системы уравнений правдоподобия:
. Поэтому критические значения определяются из системы уравнений правдоподобия:
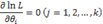 где
где 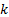 – число оцениваемых параметров.Данный метод дает состоятельные оценки. Если существует эффективная оценка, то метод максимального правдоподобия дает эту оценку. Оценки максимального правдоподобия асимптотически эффективны и имеют асимптотически нормальное распределение.
– число оцениваемых параметров.Данный метод дает состоятельные оценки. Если существует эффективная оценка, то метод максимального правдоподобия дает эту оценку. Оценки максимального правдоподобия асимптотически эффективны и имеют асимптотически нормальное распределение.
47 интервальные оценки и их св-ва


47 


48.Понятие статистической гипотезы.
Виды гипотез. Ошибки первого и второго рода
Гипотеза - это предположение о некоторых свойствах изучаемых явлений. Под статистической гипотезой понимают всякое высказывание о генеральной совокупности, которое можно проверить статистически, то есть опираясь на результаты наблюдений в случайной выборке. Рассматривают два вида статистических гипотез: гипотезы о законах распределения генеральной совокупности и гипотезы о параметрах известных распределений.
Так, гипотеза о том, что затраты времени на сборку узла машины в группе механических цехов, выпускающих продукцию одного наименования и имеющих примерно одинаковые технико-экономические условия производства, распределяются по нормальному закону, является гипотезой о законе распределения. А гипотеза о том, что производительность труда рабочих в двух бригадах, выполняющих одну и ту же работу в одинаковых условиях, не различается (при этом производительность труда рабочих каждой бригады имеет нормальный закон распределения), является гипотезой о параметрах распределения.
Подлежащая проверке гипотеза называется нулевой, или основной, и обозначается Н0. Нулевой гипотезе противопоставляют конкурирующую, или альтернативную, гипотезу, которую обозначают Н1. Как правило, конкурирующая гипотеза Н1 является логическим отрицанием основной гипотезы Н0.
Примером нулевой гипотезы может быть следующая: средние двух нормально распределенных генеральных совокупностей равны, тогда конкурирующая гипотеза может состоять из предположения, что средние не равны. Символически это записывается так:
Н0: М(Х) = М(Y); Н1: М(Х) 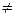 М(Y) .
М(Y) .
Если нулевая (выдвинутая) гипотеза будет отвергнута, то имеет место конкурирующая гипотеза.
Различают гипотезы простые и сложные. Если гипотеза содержит только одно предположение, то это - простая гипотеза. Сложная гипотеза состоит из конечного или бесконечного числа простых гипотез.
Например, гипотеза Н0: p = p0 (неизвестная вероятность p равна гипотетической вероятности p0) - простая, а гипотеза Н0: p < p0 - сложная, она состоит из бесчисленного множества простых гипотез вида Н0: p = pi , где pi - любое число, меньше p0 .
Выдвигаемая статистическая гипотеза может быть правильной или неправильной, поэтому необходимо ее проверить, опираясь на результаты наблюдений в случайной выборке; проверку производят статистическими методами, поэтому ее называют статистической.
При проверке статистической гипотезы пользуются специально составленной случайной величиной, называемой статистическим критерием (или статистикой). Принимаемое заключение о правильности (или неправильности) гипотезы основывается на изучении распределения этой случайной величины по данным выборки. Поэтому статистическая проверка гипотез имеет вероятностный характер: всегда существует риск допустить ошибку при принятии (отклонении) гипотезы. При этом возможны ошибки двух родов.
Ошибка первого рода состоит в том, что будет отвергнута нулевая гипотеза, хотя на самом деле она верна.
Ошибка второго рода состоит в том, что будет принята нулевая гипотеза, хотя в действительности верна конкурирующая.
В большинстве случаев последствия указанных ошибок неравнозначны. Что лучше или хуже - зависит от конкретной постановки задачи и содержания нулевой гипотезы. Рассмотрим примеры. Допустим, что на предприятии о качестве продукции судят по результатам выборочного контроля. Если выборочная доля брака не превышает заранее установленной величины p0, то партия принимается. Другими словами, выдвигается нулевая гипотеза: Н0: p 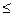 p0. Если при проверке этой гипотезы допущена ошибка 48первого рода, то мы забракуем годную продукцию. Если же совершена ошибка второго рода, то потребителю будет отправлен брак. Очевидно, что последствия ошибки второго рода могут быть значительно более серьезными.
p0. Если при проверке этой гипотезы допущена ошибка 48первого рода, то мы забракуем годную продукцию. Если же совершена ошибка второго рода, то потребителю будет отправлен брак. Очевидно, что последствия ошибки второго рода могут быть значительно более серьезными.
Другой пример можно привести из области юриспруденции. Будем рассматривать работу судей как действия по проверке презумпции невиновности подсудимого. В качестве основной проверяемой гипотезы следует рассмотреть гипотезу Н0: подсудимый невиновен. Тогда альтернативной гипотезой Н1является гипотеза: обвиняемый виновен в совершении преступления. Очевидно, что суд может совершить ошибки первого или второго рода при вынесении приговора подсудимому. Если допущена ошибка первого рода, то это означает, что суд наказал невиновного: подсудимому был вынесен обвинительный приговор, когда на самом деле он не совершал преступления. Если же судьи допустили ошибку второго рода, то это значит, что суд вынес оправдательный приговор, когда на самом деле обвиняемый виновен в совершении преступления. Очевидно, что последствия ошибки первого рода для обвиняемого будут значительно более серьезными, в то время как для общества наиболее опасными являются последствия ошибки второго рода.
Вероятность совершить ошибку первого рода называют уровнем значимости критерия и обозначают 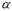 .
.
В большинстве случаев уровень значимости критерия 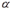 принимают равным 0,01 или 0,05. Если, например, уровень значимости принят равным 0,01, то это означает, что в одном случае из ста имеется риск допустить ошибку первого рода (то есть отвергнуть правильную нулевую гипотезу).
принимают равным 0,01 или 0,05. Если, например, уровень значимости принят равным 0,01, то это означает, что в одном случае из ста имеется риск допустить ошибку первого рода (то есть отвергнуть правильную нулевую гипотезу).
Вероятность совершить ошибку второго рода обозначают 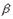 . Вероятность
. Вероятность 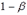 не совершить ошибку второго рода, то есть отвергнуть нулевую гипотезу, когда она неверна, называется мощностью критерия.
не совершить ошибку второго рода, то есть отвергнуть нулевую гипотезу, когда она неверна, называется мощностью критерия.
Статистическую гипотезу проверяют с помощью специально подобранной случайной величины, точное или приближенное распределение которой известно (обозначим ее К). Эту случайную величину называют статистическим критерием (или просто критерием).
Существуют различные статистические критерии, применяемые на практике: U- и Z-критерии (эти случайные величины имеют нормальное распределение); F-критерий (случайная величина распределена по закону Фишера - Снедекора); t-критерий (по закону Стьюдента); 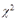 -критерий (по закону "хи-квадрат") и др.
-критерий (по закону "хи-квадрат") и др.
Множество всех возможных значений критерия можно разбить на два непересекающихся подмножества: одно из них содержит значения критерия, при которых нулевая гипотеза принимается, а другое - при которых она отвергается.
Множество значений критерия, при которых нулевая гипотеза отвергается, называется критической областью. Будем обозначать критическую область через W.
Множество значений критерия, при которых нулевая гипотеза принимается, называется областью принятия гипотезы (или областью допустимых значений критерия). Будем обозначать эту область как 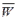 .
.
Для проверки справедливости нулевой гипотезы по данным выборок вычисляют наблюдаемое значение критерия. Будем обозначать его Кнабл.
Основной принцип проверки статистических гипотез можно сформулировать так: если наблюдаемое значение критерия попало в критическую область (то есть 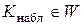 ), то нулевую гипотезу отвергают; если же наблюдаемое значение критерия попало в область принятия гипотезы (то есть
), то нулевую гипотезу отвергают; если же наблюдаемое значение критерия попало в область принятия гипотезы (то есть 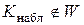 ), то нет оснований отвергать нулевую гипотезу.
), то нет оснований отвергать нулевую гипотезу.
49Пусть генеральные совокупности X и Y распределены нормально. По независимым выборкам с объемами, соответственно равными n1 и n2, извлеченным из этих совокупностей, найдены исправленные выборочные дисперсии sx2 и sy2. Требуется по исправленным дисперсиям при заданном уровне значимости α проверить нулевую гипотезу, состоящую в том, что генеральные дисперсии рассматриваемых совокупностей равны между собой: H0:D(X)=D(Y)Учитывая, что исправленные дисперсии являются несмещенными оценками генеральных дисперсий , т. е. Μ[sx2]=D(X) и Μ[sy2]=D(Y) нулевую гипотезу можно записать так: H0:Μ[sx2]=Μ[sy2]Таким образом, требуется проверить, что математические ожидания исправленных выборочных дисперсий равны между собой. Такая задача ставится потому, что обычно исправленные дисперсии оказываются различными. Возникает вопррс: значимо (существенно) или незначимо различаются исправленные дисперсии?Если окажется, что нулевая гипотеза справедлива, т. е. генеральные дисперсии одинаковы, то различие исправленных дисперсий незначимо и объясняется случайными причинами, в частности случайным отбором объектов выборки.В качестве критерия проверки нулевой гипотезы о равенстве генеральных дисперсий примем отношение большей исправленной дисперсии к меньшей, т. е. случайную величину F= Sб2/Sм2Величина F при условии справедливости нулевой гипотезы имеет распределение Фишера - Снедекора со степенями свободы k1=n1-1 и k2=n2-1, где n1- объем выборки, по которой вычислена большая исправленная дисперсия, n2 - объем выборки, по которой найдена меньшая дисперсия. Напомним, что распределение Фишера - Снедекора зависит только от чисел степеней свободы и не зависит от других параметров.Критическая область строится в зависимости от вида конкурирующей гипотезы.Первый случай. Нулевая гипотеза H0:D(X)=D(Y). Конкурирующая гипотеза H1:D(X)>D(Y).В этом случае строят одностороннюю, а именно правостороннюю, критическую область, исходя из требования, чтобы вероятность попадания критерия F в эту область в предположении справедливости нулевой гипотезы была равна принятому уровню значимости: P[F>Fкр(α; k1, k2 )]= α.Критическую точку Fкр(α; k1, k2 ) находят по таблице критических точек распределения Фишера - Снедекора, и тогда правосторонняя критическая область определяется неравенством F>Fкр, а область принятия нулевой гипотезы - неравенством F<Fкр.Обозначим отношение большей исправленной дисперсии к меньшей, вычисленное по данным наблюдений, через Fнабл и сформулируем правило проверки нулевой гипотезы.Правило 1. Для того чтобы при заданном уровне значимости проверить нулевую гипотезу H0:D(X)=D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H1:D(X)>D(Y), надо вычислить отношение большей исправленной дисперсии к меньшей, т. е. Fнабл=sб2/sм2, и по таблице критических точек распределения Фишера - Снедекора, по заданному уровню значимости α и числам степеней свободы k1 и k2 (k1 -число степеней свободы большей исправленной дисперсии) найти критическую точку Fнабл(α; k1, k2 ).Если Fнабл<Fкр - нет оснований отвергнуть нулевую гипотезу. Если Fнабл>Fкр - нулевую гипотезу отвергают.Второй случай. Нулевая гипотеза H0:D (X)=D(Y). Конкурирующая гипотеза H1:D(X)≠D(Y).
Таким образом, если обозначить через F1 левую границу критической области и через F2 - правую, то должны иметь место соотношения (рис.): P(F< F1) = α /2, Р (F > F2) = α /2.Мы видим, что достаточно найти критические точки, чтобы найти саму критическую область: F < F1, F > F2, а также область принятия нулевой гипотезы: F1 < F < F2. Как практически отыскать критические точки?Правую критическую точку (Fα =Fкр)=(α /2; k1,k2) находят непосредственно по таблице критических точек распределения Фишера - Снедекора по уровню значимости α /2 и степеням свободы k1 и k2..Правило 2. Для того чтобы при заданном уровне значимости а проверить нулевую гипотезу о равенстве генеральных дисперсий нормально распределенных совокупностей при конкурирующей гипотезе Н1:О(Х) ≠ D(У), надо вычислить отношение большей исправленной дисперсии к меньшей, т. е. Fнабл=sб2/sм2 и по таблице критических точек распределения Фишера-Снедекора по уровню значимости а α /2 (вдвое меньшем заданного) и числам степеней свободы k1 и k2 (k1—число степеней свободы большей дисперсии) найти критическую точку Fкр(α /2; k1, k2).Если Fнабл<Fкр -нет оснований отвергнуть нулевую гипотезу. Если Fнабл>Fкр -нулевую гипотезу отвергают.
50.Проверка гипотез о законе распределения.
Проверку гипотезы о законе распределения (то есть, соответствует ли выборочная совокупность какому либо определённому распределению) проводят с помощью критерия соответствия 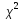 (предложен К.Пирсоном в 1900г.).
(предложен К.Пирсоном в 1900г.).
Критерий Пирсона ().
Н0заключается в том, что различие между наблюдаемыми экспериментальными частотами mi попадания вариант выборки в интервалы вариационного ряда от вычисленных теоретических частот mi теор=mi·Pi теор не достоверно (т.е. носит случайный характер). Другими словами:
Н0: экспериментальные данные соответствуют предложенному теоретическому закону распределения.
Экспериментальное значение критерия вычисляется по формуле:

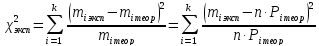
где 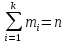 -- объём выборки, к -- количество интервалов,
-- объём выборки, к -- количество интервалов,
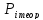 -- вероятность попадания в интервал для теоретического распределения.
-- вероятность попадания в интервал для теоретического распределения.
Затем, по таблице критерия Пирсона для заданного уровня значимости α и числа степеней свободы 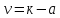 , где а -- число наложенных связей, находим
, где а -- число наложенных связей, находим 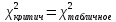 .
.
если теоретическое распределение произвольное, то а=1, 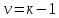
если теоретическое распределение распределено по нормальному закону Гаусса, то а=3 -- числу параметров, необходимых для вычисления вероятности: М[X],D[X] и σ[X],. следовательно 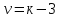
Если 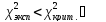 Н0 принимаем.
Н0 принимаем.
Вывод: экспериментальное распределение соответствует теоретическому.
Если 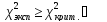 Н0 отвергаем.
Н0 отвергаем.
Вывод: экспериментальное распределение не соответствует теоретическому.
51.Суть метода наименьших квадратов (мнк).
Задача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных а и b 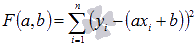 принимает наименьшее значение. То есть, при данныха и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
принимает наименьшее значение. То есть, при данныха и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов.
Таким образом, решение примера сводится к нахождению экстремума функции двух переменных.
Вывод формул для нахождения коэффициентов.
Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 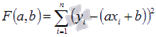 по переменныма и b, приравниваем эти производные к нулю.
по переменныма и b, приравниваем эти производные к нулю. 
Решаем полученную систему уравнений любым методом (например методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК). 
При данных а и b функция 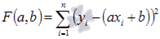 принимает наименьшее значение. Доказательство этого факта приведенониже по тексту в конце страницы .
принимает наименьшее значение. Доказательство этого факта приведенониже по тексту в конце страницы .
Вот и весь метод наименьших квадратов. Формула для нахождения параметра a содержит суммы 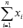 ,
, 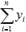 ,
, 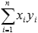 ,
, 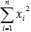 и параметрn - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a.
и параметрn - количество экспериментальных данных. Значения этих сумм рекомендуем вычислять отдельно. Коэффициент b находится после вычисления a.
52.Регрессионный анализ
Основная особенность регрессионного анализа: при его помощи можно получить конкретные сведения о том, какую форму и характер имеет зависимость между исследуемыми переменными.
Последовательность этапов регрессионного анализа
Рассмотрим кратко этапы регрессионного анализа.
Формулировка задачи. На этом этапе формируются предварительные гипотезы о зависимости исследуемых явлений.Определение зависимых и независимых (объясняющих) переменных.Сбор статистических данных. Данные должны быть собраны для каждой из переменных, включенных в регрессионную модель.
Формулировка гипотезы о форме связи (простая или множественная, линейная или нелинейная).
Определение функции регрессии (заключается в расчете численных значений параметров уравнения регрессии)
Оценка точности регрессионного анализа.Интерпретация полученных результатов. Полученные результаты регрессионного анализа сравниваются с предварительными гипотезами. Оценивается корректность и правдоподобие полученных результатов.
Предсказание неизвестных значений зависимой переменной.
При помощи регрессионного анализа возможно решение задачи прогнозирования и классификации. Прогнозные значения вычисляются путем подстановки в уравнение регрессии параметров значений объясняющих переменных. Решение задачи классификации осуществляется таким образом: линия регрессии делит все множество объектов на два класса, и та часть множества, где значение функции больше нуля, принадлежит к одному классу, а та, где оно меньше нуля, - к другому классу.
Задачи регрессионного анализа
Операции над событиями. Алгебра событий.
Алгебра событий – это множество S=2^n элементов, в которых содержатся операции умножения и сложения.
А) Объединяя благоприятствующие события А и В исходы, мы получаем подмножества во множестве W, то есть событие которое называется суммой событий А и В , и обозначается: А 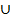 В.
В.
Б) Выбирая благоприятствующие исходы, одновременно принадлежащие и событию А, и событию В, мы получаем некоторое подмножество пустое (в случае если А и В несовместна) или непустое (А и В совместны), которое называется произведением А и В, и обозначается А 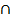 В.
В.
Дадим аксиоматическое определение вероятности любого события, входящего в алгебру S (для случая конечного n-исходов опыта). Определяем через постулаты:
1) Каждому элементарному исходу wi (i 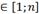 ) поставим в соответствие некоторым разумным способом положительное число Р(wi).
) поставим в соответствие некоторым разумным способом положительное число Р(wi).
2) Сумма всех положительных чисел Р(wi) , где i  , равна 1. Каждое из этих чисел называется вероятностью соответствующего исхода.
, равна 1. Каждое из этих чисел называется вероятностью соответствующего исхода.
3) Вероятность любого события, связанного с данным опытом, а значит включенного в алгебру S, равна сумме вероятностей исходов, приводящих к этому событию, то есть благоприятствующих исходов.

Аксиомы Колмогорова. Аксиоматическая теория Колмогорова основывается на пяти аксиомах, с помощью которых вводятся понятия вероятности и некоторые их свойства как для конечного множества элементарных событий, так и для любого бесконечного множества. Вот эти аксиомы:
1. Каждому событию А, принадлежащему F, ставится в соответствие неотрицательное число Р(А), которое называется вероятностью события А.
2. Вероятность достоверного события Р(F) = 1.
3. Вероятность невозможного события Р(Ø) = 0.
4. Аксиома сложения. Если  попарно не совместны, то
попарно не совместны, то 
5. Расширенная аксиома сложения. Если  попарно не совместны, то
попарно не совместны, то  (Здесь счетное множество действий).
(Здесь счетное множество действий).
Определение 3. Пространство элементарных событий Ω, σ-алгебра событий F и вероятность Р(·) на F, удовлетворяющие 5-ти аксиомам вероятности определяют вероятностное пространство, обозначаемое (Ω, F, P).
