Определение площади участков местности

Геометрический способ

Существует три способа определения площади участков: геометрический, аналитический и механический. На местности применяют два первых способа, на картах и планах - все три способа.

Геометрический способ - это вычисление площади геометрических фигур по длинам сторон и углам между ними, значения которых можно получить только из измерений.

Сначала рассмотрим простейшую фигуру - треугольник.

Формулы для вычисления площади треугольника известны:

P = 0.5 * a * h; (6.1)

P = 0.5 * a * b * Sin(C) (6.2)

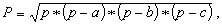(6.3)

в этих формулах:
a, b, c - длины сторон треугольника,
A, B, C - углы при вершинах против соответствующих сторон,
h - высота, проведенная из вершины A на сторону a,
p - полупериметр, p=0.5*(a + b + c).

Для решения любого n-угольника нужно знать (2*n - 3) его элементов, причем количество известных углов не должно быть больше (n-1), так как один угол всегда может быть вычислен, если остальные углы известны, на основании формулы:

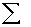β = 180o * ( n - 2 ) (6.4)

При расчете ошибки определения площади следует учитывать ошибки всех (2n-3) измеряемых элементов.

В треугольнике нужно знать (измерить) три элемента. Формула (6.1) содержит всего два элемента; это значит, что прямой угол между основанием и высотой нужно отдельно обеспечить с необходимой точностью, что равнозначно одному измерению.

Примем относительную ошибку площади mp/P = 1/1000, тогда для применения формулы (6.1) на основании принципа равных влияний необходимо выполнить условия:

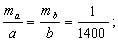
и

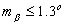
где ma,mb,β - ср.кв. ошибки сторон a, b и прямого угла между основанием и высотой.

Для формулы (6.2) на основании принципа равных влияний можно написать:

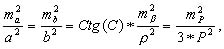(6.5)

Считая попрежнему mp/P=1/1000, получим:

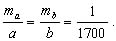
и mβ= 3.4' при < C = 60o,
mβ= 2.0' при < C = 45o,
mβ= 1.0' при < C = 26o.

Если в треугольнике измерять три стороны с относительной ошибкой mS/S и для вычисления площади применять формулу (6.3), то для равностороннего треугольника получим:

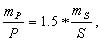(6.6)

что при mp/P=1/1000 дает ms/S=1/1500.

Таким образом, вариант с измерением трех сторон треугольника оказывается самым эффективным, так как в нем не требуется измерять углы.

Четырехугольник, как геометрическая фигура, может быть параллелограммом, ромбом, трапецией, прямоугольником, квадратом; но как участок местности его следует считать фигурой произвольной формы, так как обеспечение геометрических свойств той или иной фигуры на местности требует дополнительных измерений.

В четырехугольнике (n=4) нужно измерить пять элементов: три угла и две стороны или два угла и три стороны или один угол и четыре стороны или четыре стороны и одну диагональ. Последний вариант является наиболее предпочтительным, так как, во-первых, в нем не нужно измерять углы, и, во-вторых, согласно формуле:

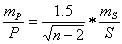(6.7)

относительная ошибка площади примерно равна относительной ошибке измерения сторон. Во всех остальных вариантах при оценке точности площади нужно учитывать как ошибки измерения сторон, так и ошибки измерения углов.

Применение геометрического способа на местности требует разбиения участка на простые геометрические фигуры, что возможно лишь при наличии видимости внутри участка (рис.6.1.)

При определении площади участков на топографических планах и картах стороны и высоты треугольников, стороны и диагонали четырехугольников нужно измерять с помощью поперечного масштаба.

Для определения площади на карте или плане геометрическим способом часто используют палетку - лист прозрачной бумаги, на котором нанесена сетка квадратов или параллельных линий. Палетку с квадратами накладывают на участок и подсчитывают, сколько квадратов содержится в данном участке; неполные квадраты считают отдельно, переводя затем их сумму в полные квадраты. Площадь участка вычисляют по формуле:

P=n*(a*M)2, (6.8)

где a - длина стороны квадрата,
M - знаменатель масштаба карты,
n - количество квадратов на участке.

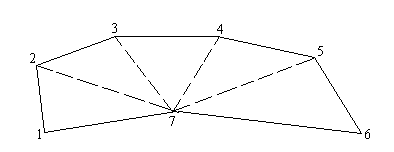
Рис.6.1

Применение палеток с параллельными линиями описано в [23].

Аналитический способ

При наличии прямоугольных координат X и Y вершин n -угольника его площадь можно вычислить по формулам аналитической геометрии; выведем одну из таких формул.

Пусть в треугольнике ABC координаты вершин равны X1 , Y1 (A), X2, Y2 (B) и X3, Y3 (C) - рис.6.2.

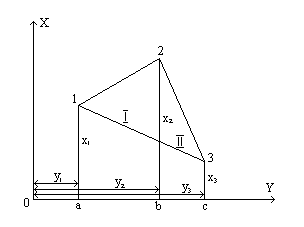
Рис.6.2

Из вершин треугольника опустим перпендикуляры на оси координат и обозначим их длину, как показано на рис.6.2.

Площадь треугольника P будет равна сумме площадей двух трапеций I(aABc) и II(bBCc) за вычетом площади трапеции III(aACc)

P=PI+PII-PIII. (6.9)

Выразим площадь каждой трапеции через ее основания и высоту:

PI=0.5(X1+X2)*(Y1-Y2);
PI=0.5(X2+X3)*(Y3-Y2); (6.10)
PI=0.5(X3+X1)*(Y1-Y3);

Чтобы избавиться от множителя 0.5, будем вычислять удвоенную площадь треугольника. Выполним умножение, приведем подобные члены, вынесем общие множители за скобки и получим:

2*P=X1*(Y2-Y3)+X2*(Y3-Y1)+X3*(Y1-Y2)

или в общем виде:

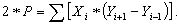(6.11)

В этой формуле индекс "i" показывает номер вершины треугольника; индекс "i" означает, что нужно брать следующую или предыдущую вершину (при обходе фигуры по часовой стрелке).

Если при группировке членов выносить за скобки Y1, то получится формула:

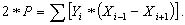(6.12)

Вычисления по обоим формулам дают одинаковый результат, поэтому на практике можно пользоваться любой из них.

Хотя формулы (6.11) и (6.12) выведены для треугольника, нетрудно показать, что они пригодны для вычисления площади любого n - угольника.

Оценка точности площади. В большинстве случаев участки на местности имеют форму неправильного n - угольника, причем количество вершин многоугольника n может быть от 30 до 20 и более. Площадь таких участков вычисляют аналитическим способом по прямоугольным координатам вершин, которые, в свою очередь, определяют в результате обработки геодезических измерений. При этом для каждой вершины многоугольника получают координаты и ошибку ее положения относительно исходных пунктов, задающих систему координат на местности.

Выведем формулу для оценки площади многоугольника по известным внутренним углам, длинам его сторон и ошибкам положения mti его вершин.

На рис.6.3 изображен фрагмент многоугольника с вершинами i-1, i, i+1, i+2 и сторонами li-1,li,li+1.

Проведем на вершинах i и i+1 окружности радиусами mti и mt(i+1) и построим биссектрисы углов βi и βi+1. Затем восстановим перпендикуляры к стороне li и найдем проекции отрезков mti и mt(i+1) на эти перпендикуляры:

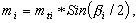(6.13)

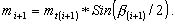(6.14)

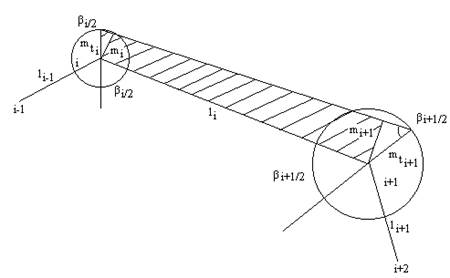
Рис.6.3

Построим трапецию, основаниями которой являются отрезки mi и mi+1, а высотой - сторона li и найдем площадь этой трапеции ΔPi. Как известно, площадь трапеции равна произведению полусуммы оснований на высоту, а поскольку основаниями трапеции являются проекции ср.кв. ошибок, то вместо полусуммы нужно взять квадратичную полусумму оснований; таким образом,

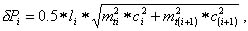(6.15)

где

c = Sin( β/2 ) .

Площадь трапеции, построенной на одной стороне многоугольника, является частью ошибки площади всего многоугольника; выполнив квадратичное суммирование площадей ΔPi по всем сторонам, получим:

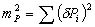
или

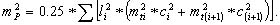(6.16)

Из формулы (6.16) можно получить формулу средней квадратической ошибки площади правильного многоугольника с одинаковой ошибкой положения mt всех его вершин:

mP=an * mt * L, (6.17)

где: L - периметр многоугольника,
an - коэффициент, зависящий от n - количества вершин;

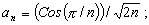
его значения:

n
an	0.204	0.250	0.256	0.250	0.243	0.231	0.222	0.212
n
an	0.205	0.197	0.179	0.156	0.143	0.128	0.091	0.065

Формула (6.17) является базовой и при оценке площади неправильных n-угольников, для которых ошибка площади mp оказывается лишь на несколько процентов больше, чем для правильного n - угольника. Так, если площадь неправильного n - угольника при том же периметре в два раза меньше площади правильного n-угольника, то ошибка его площади увеличивается лишь на 20 %.

При неодинаковых ошибках положения вершин многоугольника в формуле (6.17) достаточно вместо mt поставить mt(ср).

Примером применения формулы (6.17) является оценка площади участков, координаты вершин которых получены с топографических планов. Например, для плана масштаба 1:2000 ошибку положения точек можно принять равной mt = 0.50 мм * M = 1 м (при условии, что основа плана достаточно жесткая и ее деформацией можно пренебречь). При площади участка 0.12 га и количестве вершин n=4 (5 или 6) средняя квадратическая ошибка его площади при правильной форме (периметр L = 140 м) будет равна 35 кв.м, а при неправильной форме (периметр L>140 м) она может достигать 40 кв.м.

Другим примером применения формулы (6.17) может служить оценка площади многоугольника, координаты вершин которого получены из полярной засечки, выполненной с одного пункта-станции.

При использовании точных приборов (электронных тахеометров или систем GPS) доля ошибок измерений в ошибке положения точек значительно меньше доли ошибки их фиксации mф на местности. Приняв mti= mф, можно использовать формулу (6.17) для любых способов получения координат вершин многоугольника.

Площадь правильного n-угольника можно выразить через его периметр:

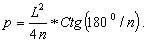(6.18)

И из формулы (6.17) получить формулу относительной ошибки площади:

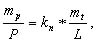(6.19)

где

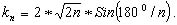(6.20)

Например:

для треугольника (n=3) mp/P = 4.24* mt/L,

для четырехугольника (n=4) mp/P = 4.00* mt/L,

для пятиугольника (n=5) mp/P = 3.72 mt/L,

для шестиугольника (n=6) mp/P = 3.46 mt/L.

Таким образом, для приближенной оценки площади 3-4-5-6- угольника в аналитическом способе можно применять формулу:

mp/P=4* mt/L; (6.21)

ошибка этой формулы может достигать 15% - 20% для участков, форма которых заметно отличается от формы правильного n -угольника.

Механический способ

Механический способ определения площади - это измерение на карте или плане площади участка с произвольными границами при помощи специального прибора - планиметра. Полярный планиметр имеет два рычага: полюсный R1 и обводной R (рис.6.4).

Один конец полюсного рычага - точка 0 - является полюсом планиметра, - на нем крепится игла; другой его конец шарнирно соединяется с обводным рычагом в точке b. На одном рычаге обводного рычага имеется счетное колесо K, которое располагается перпендикулярно рычагу, на другом конце рычага находится обводная точка f. Для механического счета числа оборотов счетного колеса имеется счетный механизм. Счетный барабан разделен на сто частей,и сбоку от него имеется верньер на одну десятую деления. Обводное колесо и счетный механизм помещаются на каретке, которую можно перемещать вдоль обводного рычага , изменяя тем самым его длину R = bf.

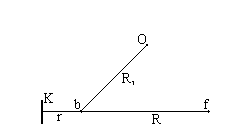
Рис.6.4

Измерение площади сводится к обводу по контуру участка на карте обводной точкой f; при этом вследствие трения о бумагу счетное колесо вращается. Берут отсчет по счетному механизму до обвода контура n1 и после обвода - n2. Площадь участка вычисляют по формуле:

P = c * ( n2 - n1 ), (6.21)

где c - цена деления планиметра.

Внешний вид полярного планиметра изображен на рис.6.5; на нем цифрами обозначены: 1 - основная каретка, 3 - полюсный рычаг, 4 - полюс, 6 - стеклянная пластинка с обводной точкой, 7 -обводной рычаг, 8 - шарнирное соединение, 9 - счетчик полных оборотов, 10 - счетное колесо, 11 - верньер.

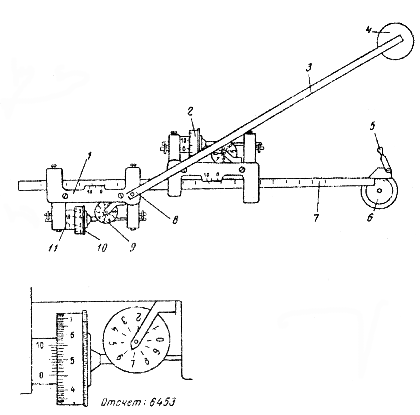
Рис.6.5

Теория полярного планиметра. Предметом теории планиметра является вывод формулы площади обводимого участка в зависимости от числа оборотов счетного колеса. При выводе формулы выделим два случая: полюс планиметра располагается внутри контура и вне контура.

Рассмотрим первый случай - полюс внутри контура. Обозначим:
R - длина обводного рычага,
R1 - длина полюсного рычага,
r -расстояние от счетного колеса до шарнира (рис.6.6).

Пусть обводная точка f движется по контуру участка и в какой -то момент занимает положение f1.

Через малый промежуток времени она займет положение f2, а точка b переместится из положения b1 в положение b2. За этот промежуток времени планиметр измерит площадь pi элементарного участка; на рисунке этот участок заштрихован. Площадь pi можно представить как сумму площадей трех фигур:

параллелограмма b1b2f'1f1 - R*hi,

кругового сектора Ob1b2 радиуса R1 - 0.5 * R12 * αi;

кругового сектора b1f'1f2 радиуса R - 0.5 * R2*β i;

pi = R * hi + 0.5 * R12 * 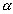i + 0.5 * R2*<β i (6.22)

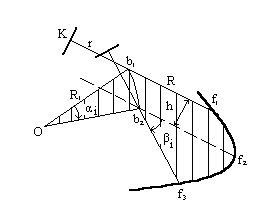
Рис.6.6

Пусть за этот промежуток времени счетное колесо повернулось на дугу si. При движении обводного рычага параллельно самому себе счетное колесо вращается полностью, а при движении обводного рычага вдоль своей оси оно не вращается, а скользит по бумаге.

Разобьем движение обводного рычага на два движения:

параллельно самому себе - колесо повернется на дугу hi ,

поворот вокруг точки b2 на угол β i - колесо повернется на дугу 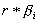в обратном направлении, поэтому:

si = hi - ,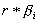

отсюда

hi = si + .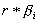

Подставим последнее выражение в формулу (6.22) и получим:

pi = R * si + R * r * bi + 0.5 * R12 * αi+ 0.5 * R2*β i.

Сложим площади элементарных участков pi и получим площадь всего измеряемого участка:

P = 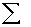pi = R * 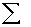si + R * r * 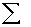bi + 0.5 * R12 * 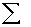αi+ 0.5 * R2* 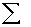β i. (6.23)

Сумма 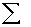si выражает дугу, на которую повернулось счетное колесо при обводе всего участка; она равна произведению разности конечного и начального отсчетов по счетному колесу на длину дуги l, соответствующей одному делению счетного колеса:

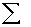si = l * (n2 - n1). (6.24)

Полюсный рычаг повернется на угол 360o или π, 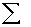αi = π, обводной рычаг повернется также на угол 360o или π, 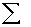β i = π.

Таким образом,

P = R * l * (n2 - n1) + π * ( R12 + R2 + 2 * R * r). (6.25)

Обозначив R * l через c и π * ( R12 + R2 + 2 * R * r) через Q, запишем:

P = c * (n2 - n1) + Q . (6.26)

Постоянная планиметра c называется ценой деления планиметра, постоянная Q - постоянным числом планиметра.

Во втором случае, когда полюс находится вне контура, все выводы повторяются, только при полном обводе контура:

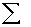α i = 0, 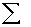β i = 0 ,

поэтому

P = c * (n2 - n1). (6.27)

Геометрический смысл постоянных планиметра.Цена деления планиметра равна площади прямоугольника со сторонами l и R. Постоянное число планиметра Q равно площади круга радиусом ρ;этот круг называется основным кругом планиметра. Радиус основного круга получим из рис.6.7. Если поставить планиметр так, чтобы плоскость счетного колеса проходила бы через полюс планиметра O и, сохраняя это положение, обвести круг радиусом ρ, то площадь этого круга будет равна:

π * ρ2= π * [(OK)2 + (r + R) 2].

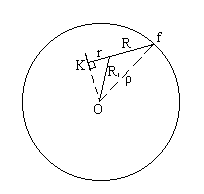
Рис.6.7

Из ΔOKB выразим (OK)2 = R12 - r2 и, подставив его значение в предыдущую формулу, получим:

π * ρ2= ( R12 + R2 + 2 * R * r) = Q.

Цену деления планиметра определяют, измеряя известную площадь, например, площадь квадрата координатной сетки. Считается, что при четырехкратном обводе трех квадратов по отдельности среднее значение цены деления получается с ошибкой около 1/1000. Точность измерения площади планиметром зависит от величины участка и от методики измерения площади. При обычной методике - двукратный обвод участка - относительная ошибка может колебаться от 1/100 до 1/300; применяя методику, известную под названием "способ Савича", для больших участков можно достичь точности измерений на уровне 11/500 - 1/10000.

Способ А.Н. Савича включает следующие операции:

разделение участка на 4 части (u1,u2, u3,u4) линиями координатной сетки; выделение в центре участка k целых квадратов координатной сетки (рис.6.8), на рисунке k = 2,

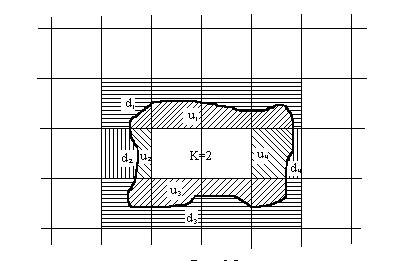
Рис.6.8

обвод каждой части участка, получение разностей Δnu1, Δnu2, Δnu3, Δnu4 отсчетов по счетному механизму (Δnui = n2 - n1),

обвод дополнения (d1, d2, d3, d4) каждой части до прямоугольника (квадрата), образованного линиями координатной сетки, получение разностей Δnd1, Δnd2, Δnd3, Δnd4,

вычисление цены деления планиметра 4 раза по формуле:

ci = ( ti * po) / ( Δnui + Δndi),

где: ti - количество квадратов координатной сетки в суммах ui + di (на рисунке t1 = t4 = 4, t2 = t3 = 1),
po - площадь квадрата координатной сетки в гектарах,
Δnui, Δndi - i-тые разности отсчетов по счетному механизму и среднего из четырех

cср = 0.25 * (c1 + c2 + c3 + c4),

вычисление площади каждой части участка p1, p2, p3, p4

pi = cср * Δnui ,

вычисление площади участка P = p1 + p2 + p3 + p4 + k * po .