Объяснить механизм возникновение вязкого трения.

Механизм внутреннего трения в жидкостях и газах заключается в том, что хаотически движущиеся молекулы переносят импульс из одного слоя в другой, что приводит к выравниванию скоростей - в результате чего импульс слоя, движущегося быстрее, уменьшается, движущегося медленнее — увеличивается, что приводит к торможению слоя, движущегося быстрее, и ускорению слоя, движущегося медленнее. Это описывается введением силы трения. Вязкость твёрдых тел обладает рядом специфических особенностей и рассматривается обычно отдельно.

Какие физические величины характеризуют вязкое трение. Их физический смысл.

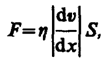где η— коэффициент динамической вязкости (коэффициент, зависящий от природы жидкости, коэффициент внутреннего трения) - характеризует сопротивление жидкости (газа) смещению ее слоёв, dv/dx— градиент скорости, показывающий быстроту изменения скорости в направлении х, перпендикулярном направлению дви­жения слоев, S—площадь, на которую действует сила F.

Виды течений и число Рейнольдса.

Для несжимаемых жидкостей наблюдается два вида течения:

- ламинарное, когда она разделяется на слои;

- турбулентное, когда жидкость перемешивается.

Английский ученый Рейнольдс установил, что характер течения зависит от безразмерной величины:

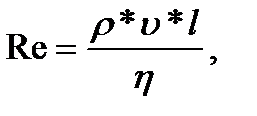
где ρ –плотность жидкости, η- коэффициент вязкости, υ – средняя скорость потока жидкости, l – характерный для поперечного сечения размер (например, сторона квадрата при квадратном сечении, радиус или диаметр при круглом сечении).

При малых значениях числа Рейнольдса наблюдается ламинарное течение. Но, начиная с некоторого значения Re называемого критическим, течение приобретает турбулентный характер. Например для круглой трубы оно равно 1000. Число Рейнольдса также считается критерием подобия течения вязкой жидкости.

Число Рейнольдса как критерий перехода от ламинарного к турбулентному режиму течения и обратно относительно хорошо действует для напорных потоков. При переходе к безнапорным потокам переходная зона между ламинарным и турбулентным режимами возрастает, и использование числа Рейнольдса как критерия не всегда правомерно. Например, в водохранилищах формально вычисленные значения числа Рейнольдса очень велики, хотя там наблюдается ламинарное течение.

Вывод расчетной формулы.

Методы определения вязкости разнообразны. Один из наиболее простых методов является метод Стокса, который применяется для маловязких жидкостей.

Пусть шарик падает в некоторой жидкости. На него действуют три силы:

A

B

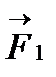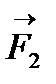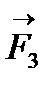Рис. 2.

1)сила тяжести F₁=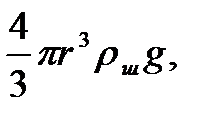

2)архимедова сила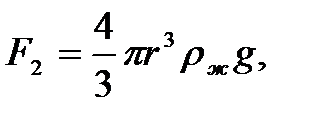

3)сила вязкого трения 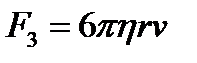(формула Стокса).

В формулах r - радиус шарика, r_ш - плотность шарика, r_ж - плотность жидкости, v - скорость шарика, h - коэффициент вязкости.

Сила вязкого трения зависит от скорости движения шарика. При свободном падении шарика в вязкой жидкости наступает момент с которого шарик движется равномерно и прямолинейно. Такое движение шарика называется установившимся. В соответствии с законами классической динамики это возможно при условии:

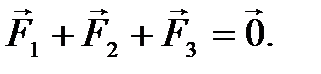(4)

В проекции на направление движения шарика:

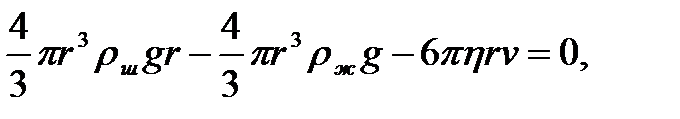(5)

Решим это уравнение относительно h

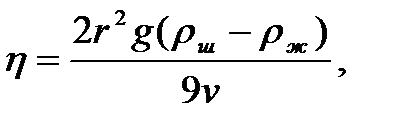(6)

где v = l/t, т.к. для средней части сосуда, ограниченной рисками А и В, где движение равномерное, l - расстояние, t - время падения шарика между рисками А и В. Подставим выражение для скорости в уравнение (6) и учтем, что r = d/2:

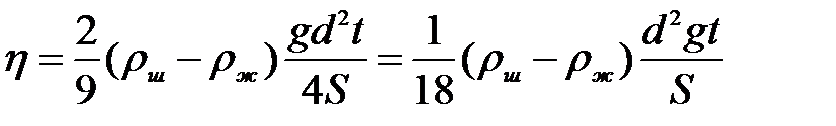. (7)

Эта формула будет расчетной в нашей лабораторной работе.

Уравнение (7) справедливо лишь тогда, когда шарик падает в безграничной среде. Если шарик падает вдоль оси трубки радиуса R, то приходится учитывать влияние боковых стенок. Поправку в формуле Стокса для такого случая теоретически обосновал Ладенбург. Формула для определения коэффициента вязкости с учетом поправок имеет вид:

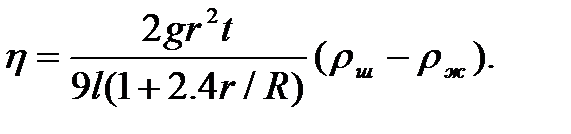
6. Какие методы определения вязкости (кроме метода Стокса) Вам известны и чем они отличаются. Содержание этих методов.

Кинематическая вязкость своим происхождением обязана классическим методам измерения вязкости: измерение времени вытекания заданного объёма через калиброванное отверстие под действием силы тяжести.

Приборы для измерения вязкости называют вискозиметрами. Обычно используют капиллярные, ротационные и шариковые вискозиметры. Наиболее распространенные капиллярные вискозиметры применяют для определения вязкости неструктурированных и слабоструктурированных жидкостей. Схема капиллярного вискозиметра была приведена на рис. 2.28. Основным элементом этих вискозиметров является капилляр. Определение вязкости проводят путем измерения времени t течения жидкости от метки a до метки b. Напряжение деформации может задаваться извне путем присоединения штуцера к моностату, в котором создается давление (или разрежение) Рм. Жидкость может вытекать также под действием гидростатического давления:

Pг = rgh, (2.4.73)

где r – плотность жидкости, g – ускорение свободного падения, h – среднее расстояние между уровнями жидкости в резервуарах А и В.

Вязкость рассчитывают по уравнению Пуазейля:

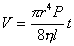, (2.4.74)

где V – объем жидкости, вытекающей из капилляра за время t; P – давление, под действием которого жидкость течет; r – радиус капилляра; l – длина капилляра. В капиллярном вискозиметре объем жидкости в резервуаре всегда постоянный, поэтому уравнение (2.4.74) приводят к виду ,

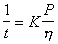(2.4.75) где K – постоянная вискозиметра, которую находят при использовании стандартной ньютоновской жидкости.