Билет 20 Дифференциальные уравнения свободных колебаний
Тройной интеграл.
Понятие тройного (а в дальнейшем – т-мерного) интеграла вводится по аналогии с двойным интегралом.
Пусть в пространстве задана некоторая область V, ограниченная замкнутой поверхностью S. Зададим в этой замкнутой области непрерывную функцию f(x, y, z). Затем разобьем область V на произвольные части Δvi , считая объем каждой части равным Δvi , и составим интегральную сумму вида 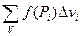 , (7.10)
, (7.10)
где точка Pi принадлежит Δvi . Пусть ρ – наибольшее расстояние между двумя точками любой части области V.
Определение 7.3. Предел при 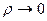 интегральных сумм (7.10), не зависящий от способа разбиения области V, называется тройным интегралом от функции f(x, y, z) по области V:
интегральных сумм (7.10), не зависящий от способа разбиения области V, называется тройным интегралом от функции f(x, y, z) по области V: 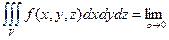
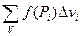 (7.11)
(7.11)
Замечание 1. Условие непрерывности подынтегральной функции не является обязатель-ным для существования кратного (двойного, тройного и т.д.) интеграла, но исследование вопросов, связанных с интегрированием разрывных функций, выходит за рамки нашего курса.
Замечание 2. Все сформулированные ранее свойства двойного интеграла можно распространить на тройной интеграл.
Замечание 3. Подобным образом можно дать определение интеграла любой кратности, рассматривая функцию п переменных, заданную в замкнутой области п-мерного пространства.
Разберем вычисление кратных интегралов на примере тройного интеграла.
Назовем трехкратным интегралом от функции f(x, y, z) по области V выражение вида:
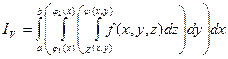 . (9.1)
. (9.1)
Трехкратный и двукратный интеграл обладают одинаковыми свойствами:
1. Если область V разбить на две области V1 и V2 плоскостью, параллельной какой-либо из координатных плоскостей, то трехкратный интеграл по области V равен сумме трехкратных интегралов по областям V1 и V2.
2. Трехкратный интеграл IV от непрерывной функции f(x,y,z) по области V равен произведению его объема V на значение функции в некоторой точке Р области V: 
Т: Тройной интеграл от функции f(x,y,z) по правильной области V равен трехкратному интегралу по той же области:

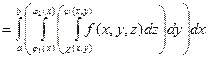 . (9.3)
. (9.3)
Замечание: изменение порядка интегрирования не меняет значения трехкратного и двукратного интегралов.
Пример. Вычислим интеграл 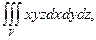 где V – треугольная пирамида с вершинами
где V – треугольная пирамида с вершинами
точках (0, 0, 0), (1, 0, 0), (0, 1, 0) и (0, 0, 1). Ее проекцией на плоскость Оху является треугольник с вершинами (0, 0), (1, 0) и (0, 1). Снизу область ограничена плоскостью z = 0, а сверху – плоскостью x + y + z = 1. Перейдем к трехкратному интегралу:
 Множители, не зависящие от переменной интегриро-вания, можно вынести за знак соответствующего интеграла:
Множители, не зависящие от переменной интегриро-вания, можно вынести за знак соответствующего интеграла:



Билет № 25. Наиболее часто к замене переменной в тройном интеграле прибегают с целью перейти от декартовой прямоугольной системы координат к цилиндрической или сферической системе. См. Цилиндрическая и сферическая системы координат.
Рассмотрим эти преобразования подробнее.
Двойной интеграл.
1. Площадь плоской области.Из формулы 7.1 следует, что при f(x,y) ≡ 0 предел интегральной суммы 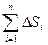 при
при 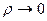 равен площади области интегрирования S, то есть
равен площади области интегрирования S, то есть 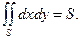 (1)
(1)
2. Объем цилиндроида.Рассмотрим тело, ограниченное частью поверхности S ( z = f(x,y) ), ограниченной контуром L, проекцией этой поверхности на плоскость Оху и отрезками, параллель-ными оси Оz и соединяющими каждую точку контура L с соответствующей точкой плоскости Оху. Такое тело будем называть цилиндроидом. Тогда из формул (7.1) и (7.2) получим, что объем этого тела равен двойному интегралу от функции f(x,y) по области S: 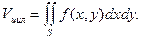 (2)
(2)
3. Площадь криволинейной поверхности.Вычислим площадь части криволинейной поверхности S, заданной уравнением z = f(x,y), ограниченной контуром L. Вспомним еще раз (см. лекцию 12), что площадь элемента поверхности ΔSi равна 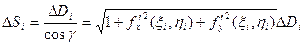
где ΔDi – проекция ΔSi на плоскость Оху, γ – угол между осью Оz и нормалью к ΔSi в некоторой ее точке 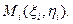 Составив интегральную сумму
Составив интегральную сумму
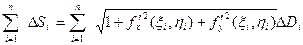
и устремив ее к пределу при 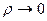 , получим формулу для площади поверхности:
, получим формулу для площади поверхности:
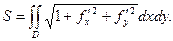
Тройной интеграл.
Объем тела.
Из определения 7.3 следует, что при f(x, y, z) ≡ 1 тройной интеграл по некоторой замкнутой области V равен объему тела V:
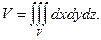 (1)
(1)
Масса тела.
Если γ = γ (x, y, z) – функция, задающая плотность вещества, из которого состоит тело V, то масса тела выражается формулой
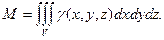 (2)
(2)
Билет 28 Механические приложения кратных интегралов
Двойной интеграл
Момент инерции плоской фигуры.Вспомним определение момента инерции
а) материальной точки М с массой т относительно точки О: I = mr² (r – расстояние от М до О);
б) системы материальных точек m1, m2,…, mn относительно точки О: 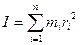
Определим теперь момент инерции относительно точки О материальной плоской фигуры D.

 у
у
ΔSi D


 ηi Pi
ηi Pi
ri
 O ξi x
O ξi x
Рис. 1.
Найдем момент инерции фигуры D (рис.1) относительно начала координат, считая, что плотность в каждой точке равна 1. Разобьем область D на части ΔSi (i = 1, 2,… n) и выберем в каждой части точку Pi (ξi, ηi). Назовем элементарным моментом инерции площадки ΔSi выражение вида ΔIi = (ξi² + ηi²)ΔSi и составим интегральную сумму
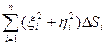 (1)
(1)
для функции f(x, y) = x² + y² по области D.
О:.Предел интегральной суммы (14.4) при 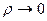 называется моментом инерции фигуры D относительно начала координат:
называется моментом инерции фигуры D относительно начала координат:
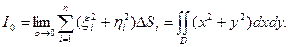 (2)
(2)
О:.Интегралы 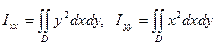
(3)
называются моментами инерции фигуры D относительно осей Ох и Оу.
Замечание. Если поверхностная плотность не равна 1, а является некоторой функци-ей γ = γ(х, у), то момент инерции фигуры относительно начала координат вычисляет-ся по формуле 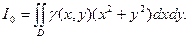 (4)
(4)
Координаты центра масс плоской фигуры.
Как известно, координаты центра масс системы материальных точек P1, P2,…, Pn с масса-ми т1, т2,…, тп определяются по формулам
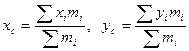 .
.
Если разбить плоскую фигуру D с поверхностной плотностью, равной 1, на части, то масса каждой части будет равна ее площади. Будем считать теперь, что вся масса эле-ментарной площадки ΔSi сосредоточена в какой-либо ее точке Pi (ξi, ηi). Тогда фигуру D можно рассматривать как систему материальных точек, центр масс которой определяется равенствами
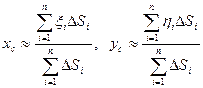 .
.
Переходя к пределу при 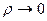 , получим точные формулы для координат центра масс плоской фигуры:
, получим точные формулы для координат центра масс плоской фигуры:
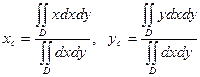 . (5)
. (5)
В случае переменной поверхностной плотности γ = γ (х, у) эти формулы примут вид
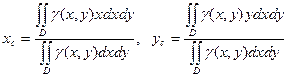 .
.
Тройной интеграл
1. Момент инерции тела.
Используя формулы для моментов инерции точки М(x, y, z) массы т относительно координатных осей:
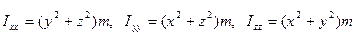
и проводя те же рассуждения, что и при определении моментов плоской фигуры, можно задать моменты инерции тела относительно координатных осей в виде:
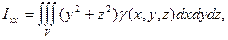
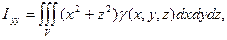 (6)
(6)
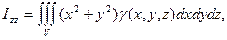
где γ (х, y, z) – плотность вещества.
2. Координаты центра масс тела.
Формулы для координат центра масс тела тоже задаются аналогично случаю плоской фигуры:
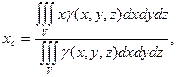
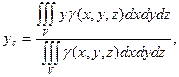
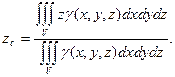 (7)
(7)
Билет № 29. Криволинейные интегралы первого и второго рода, его приложения(длина дуги, масса кривой, моменты инерции кривой, координаты центра масс кривой)
Рассмотрим на плоскости или в пространстве кривую L и функцию f, определенную в каждой точке этой кривой. Разобьем кривую на части Δsi длиной Δsi и выберем на каждой из частей точку Mi. Составим интегральную сумму 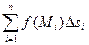 . Назовем λ длину наибольшего отрезка кривой.
. Назовем λ длину наибольшего отрезка кривой.
Определение 10.1. Если существует конечный предел интегральной суммы 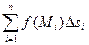 , не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом первого родаот функции f по кривой L и обозначается
, не зависящий ни от способа разбиения кривой на отрезки, ни от выбора точек Mi, то он называется криволинейным интегралом первого родаот функции f по кривой L и обозначается
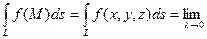
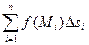 . (10.1)
. (10.1)
От пути интегрирования.
Если в каждой точке М определенной пространственной области задано значение некоторой скалярной или векторной величины, то говорят, что задано поле этой величины (соответственно скалярноеили векторное).
Рассмотрим некоторые характеристики скалярных и векторных полей.
Определение 11.1. Если в некоторой области задано скалярное поле U(x,y,z), то поверхность, определяемая уравнением
U(x, y, z) = C, (11.1)
называется поверхностью уровня. В двумерном случае линия уровня задается уравнением U(x, y) = C. (11.1`)
Определение 11.2. Если в некоторой области задано векторное поле 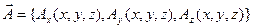 , то кривая, направление которой в каждой ее точке М совпадает с направлением вектора
, то кривая, направление которой в каждой ее точке М совпадает с направлением вектора 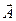 в этой точке, называется векторной линией. Она задается уравнениями
в этой точке, называется векторной линией. Она задается уравнениями
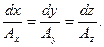 (11.2)
(11.2)
Поверхность, составленная из векторных линий, называется векторной поверхно-стью. Если векторная поверхность образована векторными линиями, проходящими через каждую точку некоторой замкнутой кривой, то она называется векторной трубкой.
Определение 11.3. Пусть задано скалярное поле U(x, y, z). Вектор
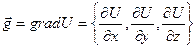 (11.3)
(11.3)
называется градиентомвеличины U в соответствующей точке (см. лекцию 4 за 2-й семестр).
Замечание. Таким образом, скалярное поле U(x, y, z) порождает векторное поле градиента gradU.
Определение 11.4. Пусть дано векторное поле 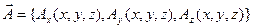 . Интеграл
. Интеграл
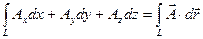 (11.4)
(11.4)
называется линейным интегралом от вектора 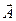 вдоль кривой L. Если кривая L замкнута, то этот интеграл называют циркуляцией вектора
вдоль кривой L. Если кривая L замкнута, то этот интеграл называют циркуляцией вектора 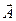 вдоль кривой L.
вдоль кривой L.
Здесь 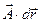 - скалярное произведение векторов
- скалярное произведение векторов 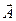 и
и 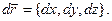
Замечание. Иногда криволинейный интеграл 2-го рода по замкнутому контуру обозначают 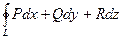 .
.
Пример. Вычислить циркуляцию векторного поля 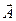 ={x, xy, xyz} вдоль контура L:
={x, xy, xyz} вдоль контура L:
x² + y² = 9, z = 2 (направление обхода контура – от точки (3,0,2) к точке (0,3,2)).
Зададим контур L параметрически: x = 3cos t, y = 3sin t, z = 2 (0 ≤ t ≤ 2π). Тогда
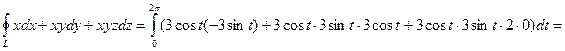
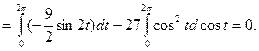
Формула Грина.
Установим связь между двойным интегралом по некоторой плоской области D и криволинейным интегралом по границе L этой области.
Пусть в плоскости Оху дана ограниченная замкнутым контуром L правильная область D. Кривые, ограничивающие эту область снизу и сверху, заданы уравнениями
y = y1(x) и y = y2(x), y1(x) ≤ y2(x), a ≤ x ≤ b (рис.1).
 y
y







 P
P
y=y2(x)
M D N
y=y1(x)
Q
O a b x
Рис. 1.
Зададим в области D непрерывные функции P(x, y) и Q(x, y), имеющие непрерывные частные производные, и рассмотрим интеграл
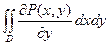 .
.
Переходя к двукратному интегралу, получим:
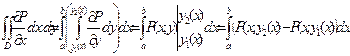 (11.5)
(11.5)
Так как у = у2(х) – параметрическое выражение кривой МPN, то
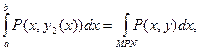
где справа стоит криволинейный интеграл по кривой MPN. Аналогично получаем, что
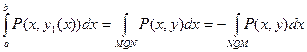 .
.
Подставим полученные результаты в формулу (11.5):
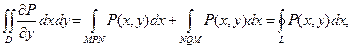 (11.6)
(11.6)
так как контур L представляет собой объединение кривых MPN и NQM.
Так же можно получить, что 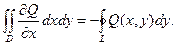 (11.7)
(11.7)
Вычтем из равенства (11.6) равенство (11.7):
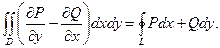
При этом обход контура L происходит по часовой стрелке. Изменим направление обхода. Тогда предыдущее равенство примет вид:
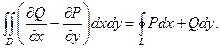 (11.8)
(11.8)
Эта формула, задающая связь между двойным интегралом и криволинейным интегралом 2-го рода, называется формулой Грина.
Замечание 1. Если в криволинейном интеграле по замкнутому контуру не указано направление обхода, то предполагается, что он производится против часовой стрелки.
Замечание 2. Если рассматривать в плоскости Оху векторное поле {P(x,y), Q(x,y)}, то в правой части формулы (11.8) стоит его циркуляция по контуру L.
От пути интегрирования.
Рассмотрим криволинейный интеграл 2-го рода 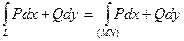 , где L – кривая, соединяющая точки M и N. Пусть функции P(x, y) и Q(x, y) имеют непрерывные частные производные в некоторой области D, в которой целиком лежит кривая L. Определим условия, при которых рассматриваемый криволинейный интеграл зависит не от формы кривой L, а только от расположения точек M и N.
, где L – кривая, соединяющая точки M и N. Пусть функции P(x, y) и Q(x, y) имеют непрерывные частные производные в некоторой области D, в которой целиком лежит кривая L. Определим условия, при которых рассматриваемый криволинейный интеграл зависит не от формы кривой L, а только от расположения точек M и N.
Проведем две произвольные кривые MPN и MQN, лежащие в области D и соединяющие точки M и N (рис.1).
 Q
Q
 • М • N Рис. 1.
• М • N Рис. 1.
P
Предположим, что 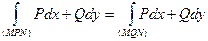 , то есть
, то есть 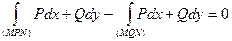
Тогда 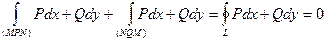 , где L – замкнутый контур, состав-ленный из кривых MPN и NQM (следовательно, его можно считать произвольным). Таким образом, условие независимости криволинейного интеграла 2-го рода от пути интегриро-вания равносильно условию, что такой интеграл по любому замкнутому контуру равен нулю.
, где L – замкнутый контур, состав-ленный из кривых MPN и NQM (следовательно, его можно считать произвольным). Таким образом, условие независимости криволинейного интеграла 2-го рода от пути интегриро-вания равносильно условию, что такой интеграл по любому замкнутому контуру равен нулю.
Билет №34. Поверхностный интеграл первого род(по площади поверхности).Приложения(масса материальной поверхности, координаты центра тяжести, моменты, площадь искривленной поверхности).
Рассмотрим незамкнутую поверхность S, ограниченную контуром L, и разобьем ее какими-либо кривыми на части S1, S2,…, Sn. Выберем в каждой части точку Mi и спроектируем эту часть на касательную плоскость к поверхности, проходящую через эту точку. Получим в проек-ции плоскую фигуру с площадью Ti. Назовем ρ наибольшее расстояние между двумя точками любой части поверхности S.
Определение 12.1. Назовем площадью S поверхностипредел суммы площадей Ti при
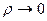 :
:
 . (12.1)
. (12.1)
Приложение поверхностного интеграла 1-го рода.
1. Площадь криволинейной поверхности, уравнение которой z = f(x, y), можно найти в виде:
 (14.21)
(14.21)
(Ω – проекция S на плоскость Оху).
2. Масса поверхности
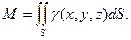 (14.22)
(14.22)
3. Моменты:
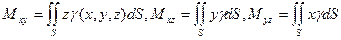 - (14.23)
- (14.23)
- статические моменты поверхности относительно координатных плоскостей Oxy, Oxz, Oyz;
 - (14.24)
- (14.24)
- моменты инерции поверхности относительно координатных осей;
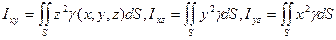 - (14.25)
- (14.25)
- моменты инерции поверхности относительно координатных плоскостей;
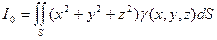 - (14.26)
- (14.26)
- момент инерции поверхности относительно начала координат.
4. Координаты центра масс поверхности:
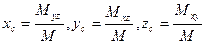 . (14.27)
. (14.27)
Билет №35. Вычисление поверхностного интеграла 1-го рода(сведение его к кратному).
Ограничимся случаем, когда поверхность S задается явным образом, то есть уравне-нием вида z = φ(x, y). При этом из определения площади поверхности следует, что
Si =  , где Δσi – площадь проекции Si на плоскость Оху, а γi – угол между осью Oz и нормалью к поверхности S в точке Mi. Известно, что
, где Δσi – площадь проекции Si на плоскость Оху, а γi – угол между осью Oz и нормалью к поверхности S в точке Mi. Известно, что
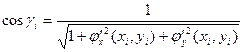 ,
,
где (xi, yi, zi) – координаты точки Mi. Cледовательно,
 .
.
Подставляя это выражение в формулу (12.2), получим, что

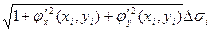 ,
,













 где суммирование справа проводится по области Ω плоскости Оху, являющейся проекцией на эту плоскость поверхности S (рис.1).
где суммирование справа проводится по области Ω плоскости Оху, являющейся проекцией на эту плоскость поверхности S (рис.1).
z
S: z=φ(x,y)
Si L
O
y
Δσi Ω
x
Рис. 1.
При этом в правой части получена интегральная сумма для функции двух переменных по плоской области, которая в пределе при 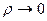 дает двойной интеграл
дает двойной интеграл 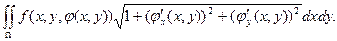 Таким образом, получена формула, позволяющая свести вычисление поверхностного интеграла 1-го рода к вычислению двойного интеграла:
Таким образом, получена формула, позволяющая свести вычисление поверхностного интеграла 1-го рода к вычислению двойного интеграла:
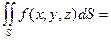
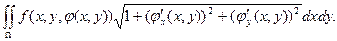 (12.5)
(12.5)
Замечание. Уточним еще раз, что в левой части формулы (12.5) стоит поверхностный интеграл, а в правой – двойной.
Билет № 36. Поверхностный интеграл второго рода. Поток векторного поля. Связь между поверхностными интегралами первого и второго рода.
Поток векторного поля.
Рассмотрим векторное поле А(М), определенное в пространственной области G, ориентированную гладкую поверхность S  G и поле единичных нормалей п(М) на выбранной стороне поверхности S.
G и поле единичных нормалей п(М) на выбранной стороне поверхности S.
Определение 13.3. Поверхностный интеграл 1-го рода
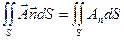 , (13.1)
, (13.1)
где An – скалярное произведение соответствующих векторов, а Ап – проекция вектора А на направление нормали, называется потоком векторного поля А(М) через выбранную сторону поверхности S.
Замечание 1. Если выбрать другую сторону поверхности, то нормаль, а, следова-тельно, и поток изменят знак.
Замечание 2. Если вектор А задает скорость течения жидкости в данной точке, то интеграл (13.1) определяет количество жидкости, протекающей в единицу времени через поверхность S в положительном направлении (отсюда общий термин «поток»).
Виды векторных полей
1.Векторные поля на прямой. Любую вещественнозначную функцию вещественного переменного можно интерпретировать как одномерное векторное поле. 2.Векторные поля на плоскости. Если 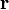 — радиус-вектор, который в заданной системе координат имеет вид
— радиус-вектор, который в заданной системе координат имеет вид 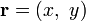 , то векторное поле описывается вектор-функцией вида:
, то векторное поле описывается вектор-функцией вида:
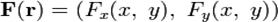
Формула Стокса.
Рассмотрим поверхность S такую, что любая прямая, параллельная оси Оz, пересекает ее в одной точке. Обозначим границу поверхности λ и выберем в качестве положительного направления нормали такое, при котором она образует с положительным направлением оси Оz острый угол. Если уравнение поверхности имеет вид z = f(x, y), то направляющие косинусы нормали задаются формулами
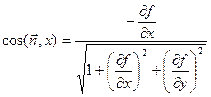 ,
, 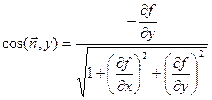 ,
,
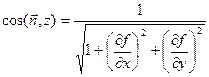 .
.
Рассмотрим некоторую трехмерную область V, в которой целиком лежит поверхность S, и зададим в этой области функцию P(x, y, z), непрерывную вместе с частными производны-ми первого порядка. Вычислим криволинейный интеграл 2-го рода по кривой λ:

 z
z 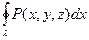 .
.
 n
n










 σ
σ
λ
O y
 D
D
x L
Рис. 2.
Уравнение линии λ имеет вид z = f(x, y), где х, у – координаты точек линии L, являющейся проекцией λ на плоскость Оху (рис.2). Поэтому, используя формулу (10.8), получаем:
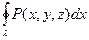 =
= 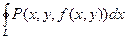 .
.
Обозначим P(x, y) = P(x, y, f(x, y)), Q(x, y) = 0 и применим к интегралу, стоящему в правой части предыдущего равенства, формулу Грина:
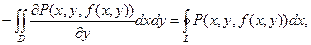
где область D ограничена линией L. Преобразуем левое подынтегральное выражение, используя формулу производной сложной функции:
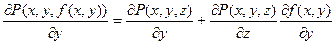
и подставим его в предыдущее равенство:
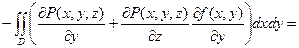
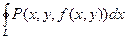 . Тогда
. Тогда
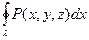 =
= 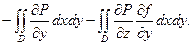 Теперь применим к интегралам, стоящим справа, формулу (13.7) и перейдем к поверхностным интегралам 1-го рода по поверхно-сти σ:
Теперь применим к интегралам, стоящим справа, формулу (13.7) и перейдем к поверхностным интегралам 1-го рода по поверхно-сти σ:
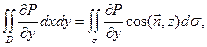
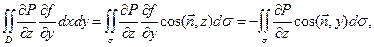
так как 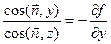 . Следовательно, окончательный результат преобразований выглядит так:
. Следовательно, окончательный результат преобразований выглядит так:
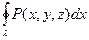 =
= 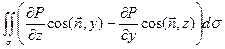 .
.
При этом направление обхода контура λ выбирается соответствующим положительному направлению нормали (рис.2).
Задавая в области V непрерывно дифференцируемые функции Q(x, y, z) и R(x, y, z), можно получить для них аналогичные соотношения:
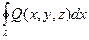 =
= 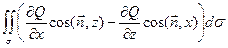 ,
,
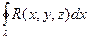 =
= 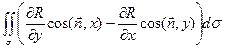 .
.
Складывая левые и правые части полученных равенств, получим формулу Стокса, уста-навливающую связь между поверхностным интегралом 1-го рода по поверхности σ и криволинейным интегралом 2-го рода по ограничивающему ее контуру λ с учетом ориен-тации поверхности:
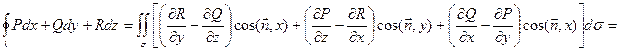
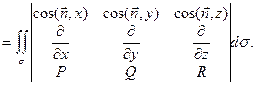 (15.6)
(15.6)
Последняя запись позволяет лучше запомнить подынтегральное выражение в правой части формулы Стокса, которое можно получить, раскрывая определитель по первой строке и учитывая, что во второй его строке стоят операторы частного дифференцирова-ния по соответствующим переменным, применяемые к функциям, стоящим в третьей строке.
Используя связь между поверхностными интегралами 1-го и 2-го рода (формула (13.9)), можно записать формулу Стокса в ином виде:
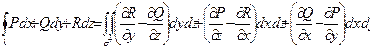 . (15.7)
. (15.7)
Ротор векторного поля.
Определение 15.2. Ротором или вектором вихрявекторного поля A = {Ax, Ay, Az}, где Ax, Ay, Az – функции от x, y, z, называется вектор, определяемый следующим образом:
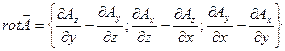 . (15.8)
. (15.8)
Замечание 1. Ротор характеризует завихренность поля А в данной точке, то есть наличие вращательных движений, так как его модуль равен удвоенной угловой скорости в этой точке.
Замечание 2. Формула Стокса в векторной формулировке имеет вид:

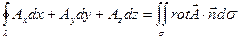 , (15.9)
, (15.9)
то есть циркуляция вектора по замкнутому контуру равна потоку ротора этого вектора через поверхность, натянутую на данный контур.
Замечание 3. Можно дать другое, инвариантное, определение ротора. Для этого рассмотрим произвольное направление п, исходящее из данной точки М, и окружим эту точку плоской площадкой σ, перпендикулярной к п и ограниченной контуром λ. Приме-няя формулу Стокса, получим:
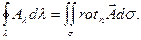
Разделив обе части этого равенства на σ и стягивая площадку σ к данной точке, найдем в пределе, что
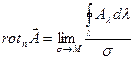 .
.
Тем самым можно определить проекцию ротора на любую ось, то есть вектор rot A не зависит от выбора координатной системы.
Билет №40. Сумма ряда. Сходимость. Ряд, составленный из членов бесконечно убывающей геометрической прогрессии. Основные свойства числовых рядов. Необходимый признак сходимости. Гармонический ряд.
Определение
Если дана бесконечная последовательность чисел 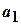 ,
, 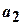 ,
, 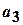 ,..., то выражение вида
,..., то выражение вида
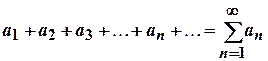 (1)
(1)
называется числовым рядом; числа 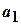 ,
, 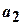 ,
, 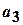 ,...– членами (элементами) ряда,
,...– членами (элементами) ряда, 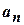 – общим членом ряда, если
– общим членом ряда, если 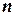 не зафиксировано.
не зафиксировано.
2 СХОДЯЩИЕСЯ И РАСХОДЯЩИЕСЯ РЯДЫ
Если дан ряд (1), то сумма первых n членов этого ряда называется 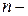 ой частичной суммой и обозначается через
ой частичной суммой и обозначается через 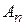 . Следовательно, суммы
. Следовательно, суммы
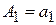 – 1-ая частичная сумма;
– 1-ая частичная сумма;
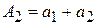 – 2-ая частичная сумма;
– 2-ая частичная сумма;
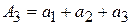 – 3-ая частичная сумма;
– 3-ая частичная сумма;
¼ – ……………………….
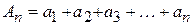 –
– 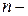 ая частичная сумма;
ая частичная сумма;
... – ……………………….
образуют последовательность частичных сумм 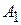 ,
, 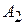 , ...,
, ..., 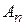 , ...
, ...
Определение
Ряд (1) называется сходящимся, если существует конечный предел последовательности частичных сумм, то есть 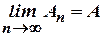 . При этом число
. При этом число 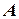 называется суммой ряда. Если для данного ряда последовательность частичных сумм
называется суммой ряда. Если для данного ряда последовательность частичных сумм 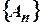 не имеет конечного предела при
не имеет конечного предела при 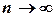 , то этот ряд называется расходящимся.
, то этот ряд называется расходящимся.
3 ОСНОВНЫЕ СВОЙСТВА СХОДЯЩИХСЯ РЯДОВ
1) Если ряд 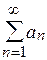 сходится, то сходится и ряд, полученный отбрасыванием из него любого конечного числа членов.
сходится, то сходится и ряд, полученный отбрасыванием из него любого конечного числа членов.
2) Пусть даны ряды 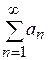 ,
, 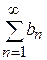 и
и 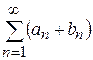 . Если оба ряда
. Если оба ряда 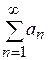 и
и 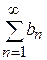 сходятся, а их суммы соответственно равны
сходятся, а их суммы соответственно равны 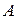 и
и 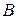 , то сходится и ряд
, то сходится и ряд 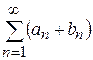 , причем его сумма равна
, причем его сумма равна 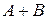 .
.
3) Если ряд 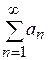 сходится и имеет сумму
сходится и имеет сумму 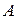 , то сходится и ряд
, то сходится и ряд 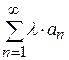 , причем его сумма равна числу
, причем его сумма равна числу 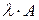 , где
, где 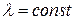 .
.
4) Если ряд 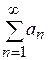 сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, не изменяющей порядок расположения членов ряда, и суммы этих рядов одинаковы. К примеру, если
сходится, то сходится и любой ряд, полученный из него группировкой слагаемых, не изменяющей порядок расположения членов ряда, и суммы этих рядов одинаковы. К примеру, если 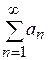 сходится и его сумма равна
сходится и его сумма равна 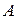 , то ряд
, то ряд
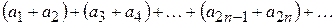
также сходится, и его сумма равна 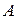 .
.
Эти свойства доказываются с помощью определения сходящихся рядов. Для примера докажем второе свойство.
Пусть 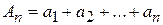 ,
, 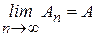 ,
,
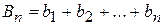 ,
, 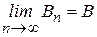 ,
,
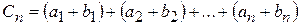 .
.
Очевидно, что при любом 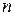
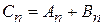 . Тогда
. Тогда 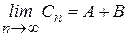 , что доказывает рассматриваемое свойство. ¨ (данный знак будет означать окончание доказательства теорем).
, что доказывает рассматриваемое свойство. ¨ (данный знак будет означать окончание доказательства теорем).
4 ПРИЗНАКИ СХОДИМОСТИ ЧИСЛОВЫХ РЯДОВ
На практике часто не столь важно найти сумму ряда, как ответить на вопрос о сходимости ряда. Для этой цели используются признаки сходимости, основанные на свойствах общего члена ряда.
НЕОБХОДИМЫЙ ПРИЗНАК СХОДИМОСТИ РЯДА
ТЕОРЕМА 1
Если ряд 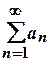 сходится, то его общий член
сходится, то его общий член 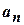 стремится к нулю при
стремится к нулю при 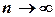 , т.е.
, т.е. 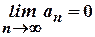 .
.
Кратко: если ряд сходится, то его общий член стремится к нулю.
Доказательство. Пусть ряд сходится и его сумма равна 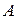 . Для любого
. Для любого 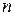 частичная сумма
частичная сумма
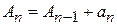
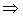
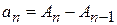 .
.
Тогда 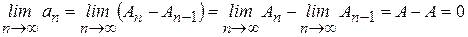 . ¨
. ¨
Из доказанного необходимого признака сходимости вытекает достаточный признак расходимости ряда: если при 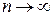 общий член ряда не стремится к нулю, то ряд расходится.
общий член ряда не стремится к нулю, то ряд расходится.
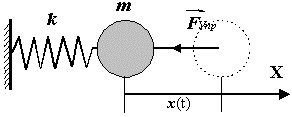
Билет 20 Дифференциальные уравнения свободных колебаний
 |
