Дифференциальная функция (функция плотности вероятности) ЗНР
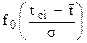 | Сотые доли | |||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,8 3,0 | 0,40 0,40 0,39 0,38 0,37 0,35 0,33 0,31 0,29 0,27 0,24 0,22 0,19 0,17 0,15 0,13 0,11 0,09 0,08 0,07 0,05 0,04 0,04 0,03 0,02 0,02 0,01 0,01 0,00 | 0,9 0,8 0,6 0,5 0,4 0,4 0,3 0,2 0,2 0,1 0,1 0,0 | 0,9 0,8 0,6 0,5 0,4 0,3 0,3 0,2 0,2 0,1 0,1 0,0 | 0,9 0,8 0,6 0,5 0,4 0,3 0,3 0,2 0,2 0,1 0,1 0,0 | 0,9 0,7 0,6 0,5 0,4 0,3 0,3 0,2 0,2 0,1 0,1 0,0 | 0,9 0,7 0,6 0,5 0,4 0,3 0,3 0,2 0,2 0,1 0,1 0,0 | 0,9 0,7 0,6 0,5 0,4 0,3 0,3 0,2 0,2 0,1 0,1 0,0 | 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,2 0,2 0,1 0,1 0,0 | 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,2 0,1 0,1 0,1 0,0 | 0,8 0,7 0,6 0,5 0,4 0,3 0,2 0,2 0,1 0,1 0,1 0,0 |
Приложение В
Дифференциальная функция (функция плотности вероятности) ЗРВ
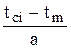 | Параметр b | ||||||
| 1,0 | 1,2 | 1,4 | 1,6 | 1,8 | 2,0 | 3,0 | |
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 | 0,91 0,82 0,74 0,67 0,61 0,55 0,50 0,45 0,41 0,37 0,33 0,30 0,27 0,25 0,22 0,20 0,18 0,17 0,15 0,14 0,12 0,11 0,10 0,09 0,08 | 0,71 0,75 0,75 0,72 0,68 0,63 0,58 0,53 0,49 0,44 0,40 0,36 0,32 0,29 0,24 0,23 0,20 0,18 0,16 0,14 0,12 0,11 0,09 0,08 0,07 | 0,54 0,66 0,72 0,74 0,73 0,70 0,66 0,62 0,57 0,52 0,46 0,41 0,37 0,32 0,28 0,25 0,21 0,18 0,16 0,13 0,11 0,09 0,08 0,07 0,06 | 0,39 0,57 0,67 0,73 0,76 0,76 0,73 0,70 0,65 0,59 0,53 0,47 0,41 0,35 0,30 0,25 0,21 0,18 0,14 0,12 0,09 0,08 0,06 0,04 0,03 | 0,28 0,47 0,61 0,71 0,78 0,80 0,80 0,77 0,72 0,66 0,59 0,52 0,45 0,38 0,31 0,26 0,21 0,16 0,13 0,10 0,07 0,05 0,04 0,03 0,02 | 0,20 0,38 0,55 0,68 0,78 0,84 0,86 0,84 0,80 0,74 0,66 0,57 0,48 0,39 0,32 0,25 0,19 0,14 0,10 0,07 0,05 0,04 0,02 0,02 0,01 | 0,03 0,12 0,26 0,45 0,66 0,87 1,04 1,15 1,17 1,10 0,96 0,77 0,56 0,38 0,23 0,13 0,06 0,03 0,01 0,00 0,00 - - - - |
Приложение Г
Коэффициент Ирвина λт
| Повторяемость информации | ||||||
| λт при α= 0,95 λт при α=0,99 | 1,5 2,0 | 1,3 1,8 | 1,2 1,7 | 1,1 1,6 | 1,0 1,5 | 0,9 1,3 |
Приложение Д
Интегральная функция (функция распределения) закона нормального распределения 
 | ||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 | 0,50 0,54 0,58 0,62 0,66 0,69 0,73 0,76 0,79 0,82 0,84 0,86 0,89 0,90 0,92 0,93 0,95 0,96 0,963 0,97 0,98 0,98 0,99 0,99 0,99 0,99 | 1,00 | 1,00 | 1,00 | 1,00 |
Приложение Е
Параметры и коэффициенты распределения Вейбулла (ЗРВ)
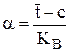 ;
;  ;
; 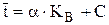
| V | b | KB | CB |
| 1,26 1,11 1,00 0,91 0,84 0,78 0,72 0,68 0,64 0,61 0,58 0,55 0,52 0,50 0,48 0,46 0,44 0,43 0,41 0,40 0,39 0,38 0,36 0,35 0,34 0,33 0,33 0,32 0,31 0,30 0,29 0,29 0,28 | 0,80 0,90 1,00 1,10 1,20 1,30 1,40 1,50 1,60 1,70 1,80 1,90 2,00 2,10 2,20 2,30 2,40 2,50 2,60 2,70 2,80 2,90 3,00 3,10 3,20 3,30 3,40 3,50 3,60 3,70 3,80 3,90 4,00 | 1,13 1,07 1,00 0,97 0,94 0,92 0,91 0,90 0,90 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,89 0,90 0,90 0,90 0,90 0,90 0,90 0,90 0,91 0,91 | 1,43 1,20 1,00 0,88 0,79 0,72 0,66 0,61 0,57 0,54 0,51 0,49 0,46 0,44 0,43 0,41 0,39 0,38 0,37 0,35 0,34 0,34 0,33 0,32 0,31 0,30 0,29 0,29 0,28 0,27 0,27 0,26 0,25 |
Приложение Ж
Интегральная функция (функция распределения) закона Вейбулла
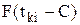
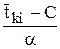 | b | ||||||||||
| 0.9 | 1.0 | 1.1 | 1.2 | 1.3 | 1.4 | 1.5 | 1.6 | 1.7 | 1.8 | 1.9 | |
| 0.1 0.2 0.3 0.4 0.5 0.6 0.7 0.8 0.9 1.0 1.1 1.2 1.3 1.4 1.5 1.6 1.7 1.8 1.9 | 0.12 0.21 0.29 0.35 0.41 0.47 0.52 0.56 0.60 0.63 0.66 0.69 0.72 0.74 0.76 0.78 0.80 0.82 0.83 | 0.10 0.18 0.26 0.33 0.39 0.45 0.50 0.55 0.59 0.63 0.67 0.70 0.73 0.75 0.78 0.80 0.82 0.84 0.85 | 0.08 0.16 0.23 0.31 0.37 0.43 0.45 0.54 0.59 0.63 0.67 0.71 0.74 0.77 0.79 0.81 0.83 0.85 0.87 | 0.06 0.14 0.21 0.28 0.35 0.42 0.48 0.54 0.59 0.63 0.67 0.71 0.75 0.78 0.80 0.83 0.85 0.87 0.89 | 0.05 0.12 0.19 0.26 0.33 0.40 0.47 0.53 0.58 0.63 0.68 0.72 0.76 0.79 0.82 0.84 0.86 0.88 0.90 | 0.04 0.10 0.17 0.24 0.32 0.39 0.46 0.52 0.58 0.63 0.68 0.73 0.76 0.80 0.83 0.86 0.88 0.90 0.91 | 0.03 0.09 0.15 0.22 0.30 0.37 0.44 0.51 0.57 0.63 0.68 0.73 0.77 0.81 0.84 0.87 0.89 0.91 0.93 | 0.03 0.07 0.14 0.21 0.28 0.36 0.43 0.50 0.57 0.63 0.69 0.74 0.78 0.82 0.85 0.88 0.90 0.92 0.94 | 0.02 0.06 0.12 0.19 0.27 0.34 0.43 0.50 0.57 0.60 0.69 0.74 0.79 0.83 0.86 0.89 0.92 0.93 0.95 | 0.02 0.05 0.11 0.18 0.25 0.33 0.41 0.49 0.56 0.63 0.70 0.75 0.80 0.84 0.87 0.90 0.93 0.94 0.96 | 0.01 0.05 0.10 0.16 0.24 0.32 0.40 0.48 0.56 0.63 0.70 0.76 0.81 0.85 0.89 0.91 0.94 0.95 0.97 |
| 2,0 2,1 2,2 2,3 2,4 2,5 2,6 2,7 2,8 2,9 3,0 3,5 4,0 | 0,85 0,86 0,87 0,88 0,89 0,90 0,91 0,91 0,92 0,93 0,93 0,95 0,97 | 0,87 0,88 0,89 0,90 0,91 0,92 0,93 0,93 0,94 0,95 0,95 0,96 0,98 | 0,88 0,90 0,91 0,92 0,93 0,94 0,94 0,95 0,96 0,96 0,97 0,98 0,99 | 0,90 0,91 0,92 0,93 0,94 0,95 0,96 0,96 0,97 0,97 0,98 0,99 1,00 | 0,92 0,93 0,94 0,95 0,96 0,96 0,97 0,97 0,98 0,98 0,99 0,99 1,00 | 0,93 0,94 0,95 0,96 0,97 0,97 0,98 0,98 0,99 0,99 0,99 0,99 1,00 | 0,94 0,95 0,96 0,97 0,98 0,98 0,99 0,99 0,99 0,99 0,99 1,00 1,00 | 0,95 0,96 0,97 0,98 0,98 0,99 0,99 0,99 0,99 1,00 1,00 1,00 1,00 | 0,96 0,97 0,98 0,99 0,99 0,99 0,99 1,00 1,00 1,00 1,00 1,00 1,00 | 0,97 0,98 0,98 0,99 0,99 0,99 1,00 1,00 1,00 1,00 1,00 1,00 1,00 | 0,98 0,98 0,99 0,99 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 1,00 |
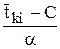 | b | |||||||||
| 2,0 | 2,1 | 2,2 | 2,3 | 2,4 | 2,5 | 2,6 | 2,7 | 2,8 | 2,9 | |
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 | 0,01 0,04 0,09 0,15 0,22 0,30 0,39 0,47 0,56 0,63 0,70 0,76 0,82 0,86 0,90 0,92 0,94 0,96 0,97 | 0,01 0,03 0,08 0,14 0,21 0,29 0,38 0,47 0,55 0,63 0,71 0,77 0,82 0,87 0,90 0,93 0,95 0,97 0,98 | 0,01 0,03 0,07 0,12 0,20 0,08 0,37 0,46 0,55 0,63 0,71 0,78 0,83 0,88 0,91 0,94 0,96 0,97 0,98 | 0,00 0,02 0,06 0,11 0,18 0,27 0,36 0,45 0,54 0,63 0,71 0,78 0,84 0,89 0,92 0,95 0,97 0,98 0,99 | 0,00 0,02 0,05 0,10 0,17 0,25 0,35 0,44 0,54 0,63 0,72 0,79 0,85 0,89 0,93 0,95 0,97 0,98 0,99 | 0,00 0,02 0,05 0,10 0,16 0,24 0,34 0,44 0,54 0,63 0,72 0,79 0,85 0,90 0,94 0,96 0,98 0,99 0,99 | 0,00 0,02 0,04 0,09 0,15 0,23 0,33 0,43 0,53 0,63 0,72 0,80 0,86 0,91 0,94 0,97 0,98 0,99 1,00 | 0,00 0,01 0,04 0,08 0,14 0,22 0,32 0,42 0,53 0,63 0,73 0,81 0,87 0,92 0,95 0,97 0,98 0,99 1,00 | 0,00 0,01 0,03 0,07 0,13 0,21 0,31 0,41 0,53 0,63 0,73 0,81 0,88 0,92 0,96 0,98 0,99 0,99 1,00 | 0,00 0,01 0,03 0,07 0,13 0,20 0,30 0,41 0,52 0,63 0,73 0,82 0,88 0,93 0,96 0,98 0,99 1,00 1,00 |
| 2,0 2,1 2,2 2,3 2,4 | 0,98 0,99 0,99 1,00 1,00 | 0,99 0,99 0,99 1,00 1,00 | 0,99 0,99 1,00 1,00 1,00 | 0,99 1,00 1,00 1,00 1,00 | 0,99 1,00 1,00 1,00 1,00 | 1,00 1,00 1,00 1,00 1,00 | 1,00 1,00 1,00 1,00 1,00 | 1,00 1,00 1,00 1,00 1,00 | 1,00 1,00 1,00 1,00 1,00 | 1,00 1,00 1,00 1,00 1,00 |
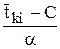 | b | |||||||||
| 3,0 | 3,1 | 3,2 | 3,3 | 3,4 | 3,5 | 3,6 | 3,7 | 3,8 | 3,9 | |
| 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 0,00 0,01 0,03 0,06 0,12 0,19 0,29 0,40 0,52 0,63 0,74 0,82 0,89 0,94 0,97 0,98 0,99 1,00 1,00 1,00 | 0,00 0,01 0,02 0,06 0,11 0,19 0,28 0,39 0,51 0,63 0,74 0,83 0,90 0,94 0,97 0,99 0,99 1,00 1,00 1,00 | 0,00 0,01 0,02 0,05 0,10 0,18 0,27 0,39 0,51 0,63 0,74 0,83 0,90 0,95 0,97 0,99 1,00 1,00 1,00 1,00 | 0,00 0,00 0,02 0,05 0,10 0,17 0,27 0,38 0,51 0,63 0,75 0,84 0,91 0,95 0,98 0,99 1,00 1,00 1,00 1,00 | 0,00 0,00 0,02 0,04 0,09 0,16 0,26 0,37 0,50 0,63 0,75 0,84 0,91 0,96 0,98 0,99 1,00 1,00 1,00 1,00 | 0,00 0,00 0,02 0,04 0,09 0,15 0,25 0,37 0,50 0,63 0,75 0,85 0,92 0,96 0,98 0,99 1,00 1,00 1,00 1,00 | 0,00 0,00 0,02 0,04 0,08 0,15 0,24 0,35 0,50 0,63 0,76 0,85 0,92 0,97 0,99 1,00 1,00 1,00 1,00 1,00 | 0,00 0,00 0,01 0,03 0,07 0,14 0,23 0,35 0,49 0,63 0,76 0,86 0,93 0,97 0,99 1,00 1,00 1,00 1,00 1,00 | 0,00 0,00 0,01 0,03 0,06 0,13 0,22 0,34 0,48 0,63 0,77 0,87 0,94 0,98 0,99 1,00 1,00 1,00 1,00 1,00 | 0,00 0,00 0,01 0,03 0,06 0,12 0,21 0,34 0,48 0,63 0,77 0,87 0,94 0,98 0,99 1,00 1,00 1,00 1,00 1,00 |
Приложение И
Критерий Колмогорова Р(λ)
| λ | Р(λ) | λ | Р(λ) | λ | Р(λ) |
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 | 1,000 1,000 1,000 1,000 0,997 0,967 0,864 | 0,7 0,8 0,9 1,0 1,1 1,2 1,3 | 0,711 0,544 0,393 0,270 0,178 0,112 0,068 | 1,4 1,5 1,6 1,7 1,8 1,9 2,0 | 0,040 0,022 0,012 0,006 0,003 0,002 0,001 |
Приложение К
Коэффициент tα, r1, r3 для двусторонних доверительных границ
| а | а=0,80 | а=0,90 | а=0,95 | ||||||
| N | tα | r1 | r3 | tα | r1 | r3 | tα | r1 | r3 |
| 1,38 1,35 1,33 1,32 1,31 1,30 1,30 1,30 1,29 1,29 | 1,61 1,45 1,37 1,33 1,29 1,24 1,21 1,19 1,16 1,14 | 0,70 0,74 0,77 0,79 0,80 0,83 0,84 0,86 0,87 0,88 | 1,83 1,76 1,73 1,71 1,70 1,68 1,68 1,67 1,66 1,66 | 1,83 1,62 1,51 1,44 1,39 1,32 1,28 1,25 1,21 1,19 | 0,64 0,68 0,72 0,74 0,76 0,78 0,80 0,82 0,84 0,86 | 2,26 2,15 2,09 2,06 2,04 2,02 2,01 2,00 1,99 1,98 | 2,09 1,79 1,64 1,55 1,48 1,40 1,35 1,31 1,27 1,28 | 0,59 0,64 0,67 0,70 0,72 0,75 0,77 0,79 0,81 0,83 |
Приложение Л
Параметр и коэффициенты закона распределения Вейбулла (ЗРВ)
| b | Kb | Cb | V | Sb | Pоп |
| 0,800 0,820 0,840 0,860 0,880 0,900 0,920 0,940 0,960 0,980 0,000 1,040 1,080 1,120 1,160 1,200 1,240 1,280 1,320 1,360 1,400 1,420 1,440 1,460 1,480 1,500 1,520 1,540 1,560 1,580 1,600 1,620 1,640 1,660 1,680 1,700 | 1,133 1,114 1,096 1,080 1,066 1,052 1,040 1,029 1,018 1,009 1,000 0,984 0,971 0,959 0,949 0,941 0,933 0,926 0,921 0,916 0,911 0,909 0,908 0,906 0,904 0,903 0,901 0,900 0,899 0,898 0,897 0,896 0,895 0,894 0,893 0,892 | 1,428 1,367 1,311 1,261 1,214 1,171 1,132 1,095 1,061 1,029 1,000 0,947 0,900 0,858 0,821 0,787 0,757 0,729 0,704 0,681 0,660 0,650 0,640 0,631 0,622 0,613 0,605 0,597 0,589 0,581 0,574 0,567 0,560 0,553 0,546 0,540 | 1,261 1,227 1,196 1,167 1,139 1,113 1,088 1,064 1,042 1,020 1,000 0,962 0,927 0,894 0,865 0,837 0,811 0,787 0,765 0,744 0,724 0,714 0,705 0,696 0,687 0,679 0,671 0,663 0,655 0,647 0,640 0,633 0,626 0,619 0,612 0,605 | 2,815 2,707 2,608 2,514 2,427 2,345 2,268 2,195 2,127 2,062 2,000 1,886 1,782 1,688 1,601 1,521 1,447 1,378 1,314 1,255 1,198 1,172 1,146 1,120 1,096 1,072 1,049 1,026 1,004 0,983 0,962 0,942 0,922 0,902 0,883 0,865 | 0,669 0,661 0,658 0,655 0,652 0,649 0,645 0,641 0,638 0,635 0,632 0,626 0,620 0,615 0,610 0,605 0,600 0,596 0,592 0,588 0,584 0,582 0,580 0,578 0,577 0,576 0,574 0,572 0,570 0,569 0,568 0,566 0,564 0,563 0,562 0,561 |
| b | Kb | Cb | V | Sb | Pоп |
| 1,720 1,740 1,760 1,780 1,800 1,820 1,840 1,860 1,880 1,900 1,920 1,940 1,960 1,980 2,000 2,020 2,040 2,060 2,080 2,100 2,120 2,140 2,160 2,180 2,200 2,220 2,240 2,260 2,280 2,300 2,320 2,340 2,360 2,380 2,400 2,420 2,440 2,460 2,480 2,500 2,520 2,540 | 0,892 0,891 0,890 0,890 0,889 0,889 0,888 0,888 0,888 0,887 0,887 0,887 0,887 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,886 0,887 0,887 0,887 0,887 0,887 0,887 0,888 | 0,534 0,528 0,522 0,517 0,511 0,506 0,501 0,496 0,491 0,486 0,481 0,476 0,472 0,468 0,463 0,459 0,455 0,451 0,447 0,443 0,439 0,436 0,432 0,428 0,425 0,421 0,418 0,415 0,412 0,408 0,405 0,402 0,399 0,396 0,393 0,391 0,388 0,385 0,382 0,380 0,377 0,374 | 0,599 0,593 0,587 0,581 0,575 0,569 0,564 0,558 0,553 0,547 0,542 0,537 0,532 0,527 0,523 0,518 0,513 0,509 0,505 0,500 0,496 0,492 0,488 0,484 0,480 0,476 0,472 0,468 0,465 0,461 0,457 0,454 0,451 0,447 0,444 0,441 0,437 0,434 0,431 0,428 0,425 0,422 | 0,847 0,829 0,812 0,795 0,779 0,763 0,747 0,731 0,716 0,701 0,687 0,672 0,658 0,645 0,631 0,618 0,605 0,592 0,579 0,567 0,555 0,543 0,531 0,520 0,509 0,498 0,487 0,476 0,465 0,455 0,444 0,434 0,424 0,415 0,405 0,395 0,386 0,377 0,368 0,359 0,350 0,341 | 0,559 0,558 0,557 0,556 0,555 0,553 0,552 0,551 0,550 0,549 0,548 0,547 0,546 0,545 0,544 0,543 0,542 0,541 0,540 0,539 0,538 0,537 0,536 0,535 0,535 0,534 0,533 0,533 0,532 0,531 0,531 0,530 0,529 0,528 0,527 0,527 0,526 0,526 0,525 0,524 0,524 0,523 |
| 2,560 2,580 2,600 2,620 2,640 2,660 2,700 2,720 2,740 2,760 2,780 2,800 2,820 2,840 2,860 2,880 2,900 2,920 2,940 2,960 2,980 3,000 3,020 3,040 3,060 3,080 3,100 3,120 3,140 3,160 3,180 3,200 2,340 2,360 2,380 2,400 2,420 2,440 2,460 2,480 2,500 2,520 | 0,888 0,888 0,888 0,888 0,889 0,889 0,889 0,889 0,890 0,890 0,890 0,891 0,891 0,891 0,891 0,892 0,892 0,892 0,892 0,893 0,893 0,893 0,893 0,894 0,894 0,894 0,895 0,895 0,895 0,895 0,896 0,896 0,886 0,886 0,886 0,886 0,887 0,887 0,887 0,887 0,887 0,887 | 0,372 0,369 0,367 0,364 0,362 0,357 0,355 0,353 0,351 0,348 0,346 0,344 0,342 0,340 0,338 0,336 0,334 0,332 0,330 0,328 0,326 0,325 0,323 0,321 0,319 0,317 0,316 0,314 0,312 0,310 0,309 0,307 0,402 0,399 0,396 0,393 0,391 0,388 0,385 0,382 0,380 0,377 | 0,419 0,416 0,413 0,410 0,407 0,402 0,399 0,397 0,394 0,392 0,389 0,387 0,384 0,382 0,379 0,377 0,375 0,372 0,370 0,368 0,366 0,363 0,361 0,359 0,357 0,355 0,353 0,351 0,349 0,347 0,345 0,343 0,454 0,451 0,447 0,444 0,441 0,437 0,434 0,431 0,428 0,425 | 0,332 0,324 0,315 0,307 0,299 0,283 0,275 0,267 0,260 0,252 0,245 0,237 0,230 0,223 0,216 0,209 0,202 0,195 0,188 0,181 0,175 0,168 0,162 0,155 0,149 0,143 0,136 0,130 0,124 0,118 0,112 0,106 0,434 0,424 0,415 0,405 0,395 0,386 0,377 0,368 0,359 0,350 | 0,522 0,521 0,520 0,520 0,519 0,518 0,517 0,517 0,516 0,516 0,515 0,514 0,514 0,513 0,513 0,512 0,512 0,511 0,511 0,510 0,510 0,509 0,509 0,508 0,508 0,507 0,507 0,507 0,506 0,506 0,505 0,505 0,530 0,529 0,528 0,527 0,527 0,526 0,526 0,525 0,524 0,524 |
| 2,540 2,560 2,580 2,600 2,620 2,640 2,660 2,700 2,720 2,740 2,760 2,780 2,800 2,820 2,840 2,860 2,880 2,900 2,920 2,940 2,960 2,980 3,000 3,020 3,040 3,060 3,080 3,100 3,120 3,140 3,160 3,180 3,200 3,240 3,260 3,280 3,300 3,320 3,340 3,360 3,380 3,400 | 0,888 0,888 0,888 0,888 0,888 0,889 0,889 0,889 0,889 0,890 0,890 0,890 0,891 0,891 0,891 0,891 0,892 0,892 0,892 0,892 0,893 0,893 0,893 0,893 0,894 0,894 0,894 0,895 0,895 0,895 0,895 0,896 0,896 0,896 0,896 0,897 0,897 0,897 0,898 0,898 0,898 0,898 | 0,374 0,372 0,369 0,367 0,364 0,362 0,357 0,355 0,353 0,351 0,348 0,346 0,344 0,342 0,340 0,338 0,336 0,334 0,332 0,330 0,328 0,326 0,325 0,323 0,321 0,319 0,317 0,316 0,314 0,312 0,310 0,309 0,307 0,304 0,302 0,301 0,299 0,298 0,296 0,295 0,293 0,292 | 0,422 0,419 0,416 0,413 0,410 0,407 0,402 0,399 0,397 0,394 0,392 0,389 0,387 0,384 0,382 0,379 0,377 0,375 0,372 0,370 0,368 0,366 0,363 0,361 0,359 0,357 0,355 0,353 0,351 0,349 0,347 0,345 0,343 0,339 0,337 0,335 0,334 0,332 0,330 0,328 0,326 0,325 | 0,341 0,332 0,324 0,315 0,307 0,299 0,283 0,275 0,267 0,260 0,252 0,245 0,237 0,230 0,223 0,216 0,209 0,202 0,195 0,188 0,181 0,175 0,168 0,162 0,155 0,149 0,143 0,136 0,130 0,124 0,118 0,112 0,106 0,095 0,089 0,083 0,078 0,072 0,067 0,061 0,056 0,051 | 0,523 0,522 0,521 0,520 0,520 0,519 0,518 0,517 0,517 0,516 0,516 0,515 0,514 0,514 0,513 0,513 0,512 0,512 0,511 0,511 0,510 0,510 0,509 0,509 0,508 0,508 0,507 0,507 0,507 0,506 0,506 0,505 0,505 0,504 0,504 0,503 0,503 0,503 0,502 0,502 0,501 0,501 |
| 3,420 3,440 3,460 3,480 3,500 3,520 3,540 3,560 3,580 3,600 3,620 3,640 3,660 3,680 3,700 3,720 3,740 3,760 3,780 3,800 3,820 3,840 3,860 3,880 3,900 3,920 3,940 3,960 3,980 4,000 4,020 4,040 4,060 4,080 4,100 4,120 4,140 4,160 4,180 4,200 | 0,899 0,899 0,899 0,899 0,900 0,900 0,900 0,901 0,901 0,901 0,901 0,902 0,902 0,902 0,902 0,903 0,903 0,903 0,903 0,904 0,904 0,904 0,905 0,905 0,905 0,905 0,906 0,906 0,906 0,906 0,907 0,907 0,907 0,907 0,908 0,908 0,908 0,908 0,909 0,909 | 0,290 0,289 0,287 0,286 0,285 0,283 0,282 0,281 0,279 0,278 0,277 0,275 0,274 0,273 0,272 0,270 0,269 0,268 0,267 0,266 0,264 0,263 0,262 0,261 0,260 0,259 0,258 0,256 0,255 0,254 0,253 0,252 0,251 0,250 0,249 0,248 0,247 0,246 0,245 0,244 | 0,323 0,321 0,320 0,318 0,316 0,315 0,313 0,312 0,310 0,308 0,307 0,305 0,304 0,302 0,301 0,299 0,298 0,297 0,295 0,294 0,292 0,291 0,290 0,288 0,287 0,286 0,284 0,283 0,282 0,280 0,279 0,278 0,277 0,276 0,274 0,273 0,272 0,271 0,270 0,268 | 0,046 0,040 0,035 0,030 0,025 0,020 0,015 0,010 0,005 0,001 -0,004 -0,009 -0,014 -0,018 -0,023 -0,027 -0,032 -0,036 -0,041 -0,045 -0,050 -0,054 -0,058 -0,062 -0,067 -0,071 -0,075 -0,079 -0,083 -0,087 -0,091 -0,095 -0,099 -0,103 -0,107 -0,111 -0,115 -0,118 -0,122 -0,126 | 0,501 0,500 0,500 0,499 0,499 0,499 0,498 0,498 0,497 0,497 0,497 0,496 0,496 0,495 0,495 0,495 0,495 0,494 0,494 0,494 0,494 0,494 0,493 0,493 0,493 0,492 0,492 0,492 0,491 0,491 0,491 0,490 0,490 0,489 0,489 0,489 0,488 0,488 0,487 0,487 |
Основы теории надежности и диагностики
Составители: Шевцов Юрий Дмитриевич
Сковородов Николай Алексеевич
Линник Геннадий Дмитриевич
Редактор У.В. Новикова
Компьютерная верстка Н.В.Василенко

Подписано в печать Формат 60х84/16
Бумага оберточная №1 Офсетная печать
Печ. л. Изд. №
Усл. печ. л. Тираж __ экз.
Уч.-изд. л. Заказ №
Цена руб.

Лицензия на издательскую деятельность: ИД № 02586 от 18.08.2000 г.
Лицензия на полиграфическую деятельность: ПД №10 – 47020 от 11.09.2000 г.
Издательство КубГТУ: 350072, Краснодар, ул. Московская, 2, кор. А
Типография КубГТУ: 350058, Краснодар, ул. Старокубанская, 88/4
