Раздел 1. Развитие понятия числа
Раздел 1. Развитие понятия числа
Самостоятельная работа № 1.
Решение заданий без точного учета погрешностей
Цель: Знать правила действия над приближенными числами без точного учета погрешностей.
Методические рекомендации
Правила для выполнения действий без точного учета погрешностей:
1. При сложении, вычитании приближенных чисел в результате следует сохранять столько десятичных знаков, сколько их имеется в данном, с наименьшим числом десятичных знаков.
2. При умножении и делении приближенных чисел в результате следует сохранять столько значащих цифр, сколько их имеется в данном с наименьшим числом значащих цифр.
3. При возведении в квадрат и куб в результате следует сохранять столько значащих цифр, сколько их имеется в основании степени.
4. При извлечении квадратных и кубических корней в результате следует сохранять столько значащих цифр, сколько их имеется в подкоренном числе.
5. При выполнении промежуточных действий в результате следует сохранять одну лишнюю (запасную) цифру, которую в окончательном результате отбрасывают.
Определение: Цифры, записанные справа от запятой, называются десятичными знаками числа.
Определение: Значащими цифрами числа называются все его верные цифры, кроме нулей, записанных левее первой отличной от нуля цифры.
Определение: Цифра 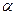 в записи приближения называется верной, если абсолютная погрешность не превышает того разряда, в котором эта цифра записана. В противном случае цифра называется сомнительной.
в записи приближения называется верной, если абсолютная погрешность не превышает того разряда, в котором эта цифра записана. В противном случае цифра называется сомнительной.
Применив правила для выполнения действий без точного учета погрешностей, выполните действия.
1. Найти сумму 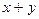 и разность
и разность  , если:
, если:
а) 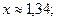
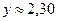 ; б)
; б)  ;
; 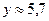 ;
;
в)  ;
; 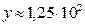 ; г)
; г) 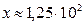 ;
; 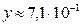
2. Найти произведение  и частное
и частное  , если
, если
а) 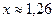 ;
;  ; б)
; б) 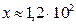 ;
; 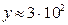 ;
;
в) 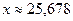 ;
; 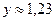 ; г)
; г)  ;
; 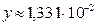
3. Найдите значение выражения 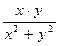 для
для  ;
; 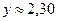 . Для вычисления рекомендуется пользоваться калькулятором.
. Для вычисления рекомендуется пользоваться калькулятором.
4. Вычислите, ответ округлите до 0,001.
| 1 вариант | 2 вариант |
а) 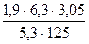 | а) 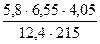 |
б) 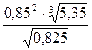 | б) 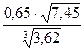 |
в) 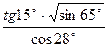 | в)  |
г) 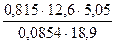 | г)  |
Самостоятельная работа № 2.
Решение заданий с точным учетом погрешности
Цель: Знать правила действия над приближенными числами с точным учетом погрешности.
Методические рекомендации
Правила для выполнения действий с точным учетом погрешности:
1. 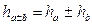 4.
4. 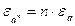
2.  5.
5. 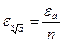
3. 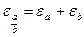
Применив правила для выполнения действий с точным учетом погрешности, выполните действия:
1. Найдите сумму 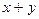 и разность
и разность  , если:
, если:
а) 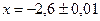 ;
; 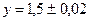
б)  ;
; 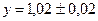
в) 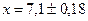 ;
; 
2. Найдите произведение  и частное
и частное  , если:
, если:
а)  с точностью до 0,5%;
с точностью до 0,5%;  с точностью до 1%;
с точностью до 1%;
б) 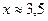 с точностью до 1%;
с точностью до 1%; 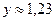 с точностью до 0,5%;
с точностью до 0,5%;
в) 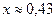 с точностью до 0,1%;
с точностью до 0,1%; 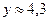 с точностью до 1%.
с точностью до 1%.
3. Масса ящика с конфетами равна 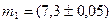 кг, масса пустого ящика равна
кг, масса пустого ящика равна  кг. Найти массу конфет.
кг. Найти массу конфет.
4. Найти площадь прямоугольника ширины 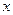 и длины
и длины 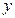 , если
, если 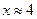 м и
м и 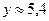 м с точностью до 1%.
м с точностью до 1%.
5. Найти степень 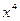 , если
, если 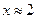 с точностью до 2,5%.
с точностью до 2,5%.
6. Найти 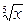 , если
, если  с точностью до 2,5%.
с точностью до 2,5%.
Самостоятельная работа № 3.
Раздел 2. Уравнения и неравенства
Самостоятельная работа № 4.
Самостоятельная работа № 5.
Самостоятельная работа № 7.
Решение заданий на преобразование логарифмических выражений
Цель: Знать основное логарифмическое тождество, свойства логарифмов, уметь применять их при преобразовании выражений.
Методические рекомендации
I. Свойства логарифмов.
1.Основное логарифмическое тождество: 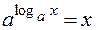
2. 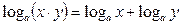
3. 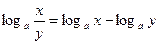
4. 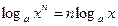
5. 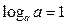
6. 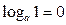
7. 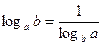
8. 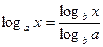 - формула перехода к другому основанию
- формула перехода к другому основанию
9. 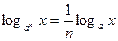
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Найдите значение числового выражения: 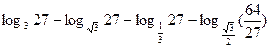 | 1. Найдите значение числового выражения: 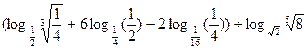 |
2. Вычислите: а) 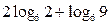 ; б) ; б) 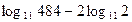 ; в) ; в) 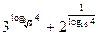 | 2. Вычислите: а) 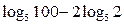 ; б) ; б) 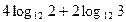 ; в) ; в) 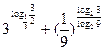 |
3. Найдите 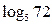 , если известно, что , если известно, что 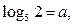 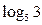 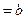 . . | 3. Вычислите 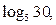 если известно, что если известно, что 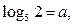 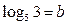 . . |
4. Вычислить: а) 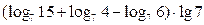 ; б) ; б) 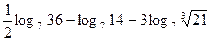 | 4. Вычислить: а) 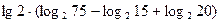 ; б) ; б) 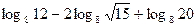 |
Самостоятельная работа № 8.
Степени чисел от 0 до 10
| n | ||||||||||||
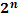 | ||||||||||||
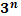 | ||||||||||||
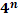 | ||||||||||||
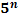 | ||||||||||||
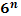 | ||||||||||||
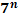 | ||||||||||||
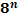 | ||||||||||||
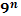 | ||||||||||||
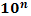 | ||||||||||||
Решение квадратных уравнений: 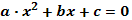 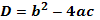 , Если , Если 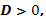 то то 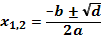 Если Если 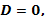 то то 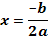 Если Если 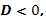 то корней нет то корней нет | Формулы сокращенного умножения: 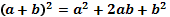 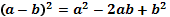 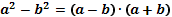 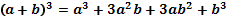 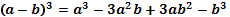 | |||||||||||
| Свойства степеней | Свойства корней n-ой степени | |||||||||||
1. 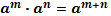 2. 2. 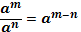 3. 3. 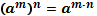 4. 4. 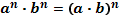 5. 5. 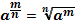 6. 6. 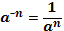 7. 7. 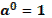 8. 8. 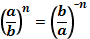 9. 9. 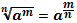 | 1. 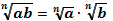 2. 2. 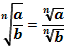 3. 3. 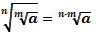 4. 4. 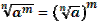 5. 5. 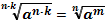 6. 6. 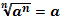 7. 7. 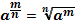 | |||||||||||
Используя предложенные методические рекомендации и методические рекомендации к самостоятельной работе №9, выполните задания:
| 1 вариант | 2 вариант |
1. Решить уравнения: а)  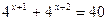 ; б) ; б) 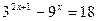 ; в) ; в) 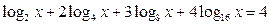 ; г) ; г) 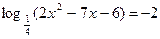 ; д) ; д) 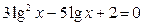 . . | 1. Решить уравнения: а) 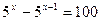 ; б) ; б) 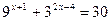 ; в) ; в) 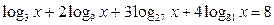 ; г) ; г) 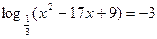 ; д) ; д) 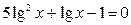 . . |
2. Решить неравенства: а) 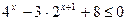 ; б) ; б) 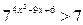 ; в) ; в) 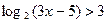 ; г) ; г) 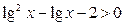 . . | 2. Решить неравенства: а) 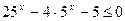 ; б) ; б) 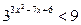 ; в) ; в) 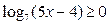 ; г) ; г) 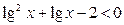 . . |
Самостоятельная работа № 9.
Подсказки.
1. Воспользуйтесь формулой двойного угла для 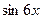 и
и 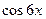 .
.
2. Обозначьте 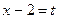 , решите уравнение, сведя его к квадратному с помощью формулы
, решите уравнение, сведя его к квадратному с помощью формулы 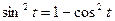 .
.
3. Сгруппируйте 1-ое и 3-е слагаемые, примените разложение на множители.
4. Воспользуйтесь формулой двойного угла для 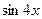 и
и 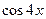 , формулой понижения степени
, формулой понижения степени 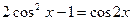 .
.
5. Раскройте скобки, примените основное тригонометрическое тождество.
6. Приведите дроби к общему знаменателю, а затем используйте основное тригонометрическое тождество 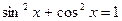 , сведите уравнение к квадратному
, сведите уравнение к квадратному
Самостоятельная работа № 10.
Решение прикладных задач
Цель: Уметь применять определение производной и ее механический смысл к решению прикладных задач.
Методические рекомендации
Физический смысл первой производной.
Физический смысл производной заключается в том, что мгновенная скорость движения 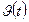 в момент времени t есть производная пути по времени, т.е.
в момент времени t есть производная пути по времени, т.е.
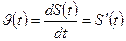
Физический смысл второй производной.
Ускорение прямолинейного движения в данный момент времени есть первая производная скорости по времени или вторая производная пути по времени.
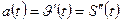
Пример.
1. Зависимость пути от времени при прямолинейном движении точки задана уравнением
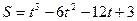 .
.
В какой момент времени ускорение движения точки будет равно 24 м/с2?
Решение.
а) Найдем скорость движения точки по формуле: 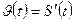
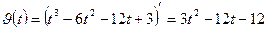
б) Найти ускорение движения точки по формуле: 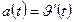
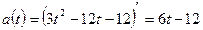
в) Из условия 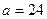 м/с2, найти момент времени:
м/с2, найти момент времени:
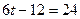
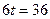
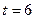 c
c
Ответ: 6 с.
v Правила дифференцирования и таблица производных основных функций.
Правила.
1. 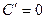 | 4. 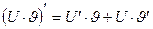 |
2. 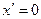 | 5. 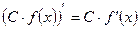 |
3. 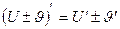 | 6. 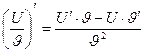 |
Производные основных элементарных функций.
1. 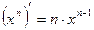 , , 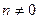 | 8. 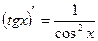 |
2. 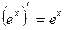 | 9. 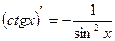 |
3. 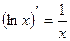 | 10. 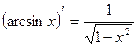 |
4. 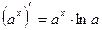 | 11. 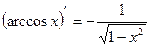 |
5. 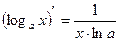 | 12. 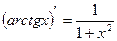 |
6. 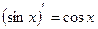 | 13. 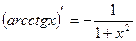 |
7. 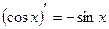 |
Используя методические рекомендации, выполните задания:
| 1 вариант | 2 вариант |
1. Тело движется вверх по закону 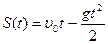 с начальной скоростью с начальной скоростью 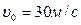 , , 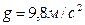 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 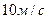 ? ? | 1. Тело движется вверх по закону 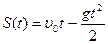 с начальной скоростью с начальной скоростью 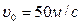 , , 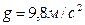 . Через сколько секунд скорость станет равной . Через сколько секунд скорость станет равной 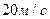 . . |
2. Найдите силу, действующую на тело массой 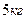 , движущееся по закону , движущееся по закону 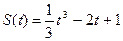 в момент времени в момент времени 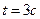 . . | 2. Тело массой 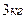 движется по прямой согласно уравнению движется по прямой согласно уравнению 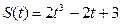 . Найдите действующую на него силу в момент времени . Найдите действующую на него силу в момент времени 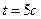 . . |
3. Определить кинетическую энергию точки, массой 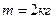 , движущейся по закону , движущейся по закону 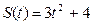 в момент времени в момент времени 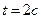 . . | 3. Определить кинетическую энергию точки, массой 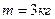 , движущейся по закону , движущейся по закону 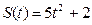 в момент времени в момент времени 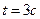 . . |
4.Точка движется по прямой по закону 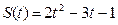 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 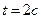 . . | 4. Точка движется по прямой по закону 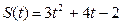 . Найти ускорение точки в момент времени . Найти ускорение точки в момент времени 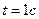 . . |
.
Самостоятельная работа № 11.
Теоретический материал
Отложим вектор так, чтобы его начало совпало с началом координат. Тогда координаты его конца называются координатами вектора. Обозначим 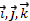 векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.
векторы с координатами (1, 0, 0), (0, 1, 0), (0, 0, 1) соответственно. Их длины равны единице, а направления совпадают с направлениями соответствующих осей координат. Будем изображать эти векторы, отложенными от начала координат и называть их координатными векторами.
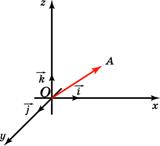
Теорема.Вектор 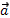 имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде
имеет координаты (x, y, z) тогда и только тогда, когда он представим в виде  .
.
Вариант 1
| № п/п | Название операции | Формулы |
| Найти сумму векторов |  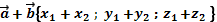 | |
| Найти разность векторов |   | |
| Найти произведение вектора на число | 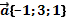 , ,    | |
| Вычислить координаты середины отрезка | Точка A 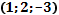 . Точка B (-3;4;-1 . Точка B (-3;4;-1  .Точка С- середина отрезка АВ. С( .Точка С- середина отрезка АВ. С( 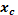 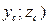  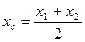  ; ; 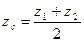 . . | |
| Найти координаты вектора | Точка A 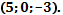 Точка B (-1;4;-7 Точка B (-1;4;-7  .Находим координаты вектора .Находим координаты вектора 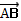 . Из координат конца вычислить координаты начала вектора . Из координат конца вычислить координаты начала вектора 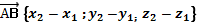 | |
| Найти длину вектора |  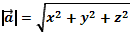 | |
| Вычислить скалярное произведение векторов |  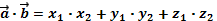 | |
| Найти косинус угла между векторами |  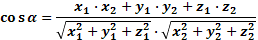 | |
При каких значениях  и и 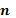 векторы коллинеарны? векторы коллинеарны? |   | |
| Проверьте перпендикулярность векторов |   - условие перпендикулярности векторов - условие перпендикулярности векторов |
Вариант 2
| № п/п | Название операции | Формулы |
| Найти сумму векторов |  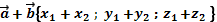 | |
| Найти разность векторов |   | |
| Найти произведение вектора на число | 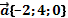 , ,  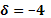  | |
| Вычислить координаты середины отрезка | Точка A  Точка B (2;-3;1 Точка B (2;-3;1  Точка С- середина отрезка АВ. С( Точка С- середина отрезка АВ. С( 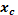 , , 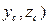  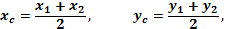 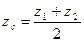 . . | |
| Найти координаты вектора | Точка A 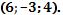 Точка B (1;-4;7 Точка B (1;-4;7  . Находим координаты вектора . Находим координаты вектора 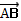 . Из координат конца вычислить координаты начала вектора . Из координат конца вычислить координаты начала вектора 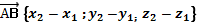 | |
| Найти длину вектора | 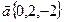 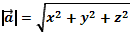 | |
| Вычислить скалярное произведение векторов |  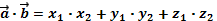 | |
| Найти косинус угла между векторами |  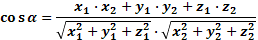 | |
При каких значениях  и и 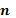 векторы коллинеарны? векторы коллинеарны? |   | |
| Проверьте перпендикулярность векторов |   - условие перпендикулярности векторов - условие перпендикулярности векторов |
Раздел 1. Развитие понятия числа
Самостоятельная работа № 1.
