Критерии устойчивости Найквиста

Критерий Найквиста позволяет судить по частотным характеристикам разомкнутой системы об устойчивости и качестве управления при замыкании системы.

Пусть W(jω) – частотная передаточная функция разомкнутой системы автоматического управления. Разомкнутую систему полагаем устойчивой. Представляем частотную передаточную функцию в виде суммы действительной и мнимой частей

W(jω) = U(ω)+jV(ω).

Критерий Найквиста формулируется следующим образом:

Если разомкнутая система устойчива, то для устойчивости замкнутой систем необходимо и достаточно, чтобы амплитудно-фазовая частотная характеристика разомкнутой системы (годограф векторной функции W(jω)) не охватывала на комплексной плоскости точку с координатами (-1+j₀).

Физический смысл критерия (во всяком случае, для простых систем) очевиден: При изменении частоты входного сигнала в пределах от нуля до бесконечности не должно быть частоты, для которой при фазовом сдвиге 180° амплитуда сигнала на выходе системы оказалась бы больше амплитуды сигнала на ее входе.

При 180-градусном сдвиге обратная связь на частоте w₀ превращается из отрицательной в положительную. Если к тому же модуль 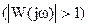, то создаются условия для возникновения колебаний на этой частоте.

Если амплитудно-фазовая частотная характеристика имеет "клювообразный" вид, то тогда числа положительных (сверху вниз) и отрицательных (снизу вверх) пересечений оси абсцисс должны быть равны. В этом случае система может оказаться неустойчивой как при увеличении так и при уменьшении коэффициента усиления в системе.

Системы, которые устойчивы при значениях общего коэффициента усиления, лежащем в определенных пределах, называются условно устойчивыми. Системы, которые устойчивы при любом значении общего коэффициента усиления, лежащем ниже некоторого максимально допустимого значения, называются абсолютно устойчивыми.

При использовании критерия устойчивости Найквиста необходимо убедиться в устойчивости разомкнутой системы. Неустойчивость разомкнутой САР может быть следствием наличия местных обратных связей. Проверка устойчивости местных замкнутых контуров может быть сделана с помощью любых критериев устойчивости (в том числе и с помощью критерия Найквиста).

Если САР астатическая, т.е. имеет интегрирующие звенья, то в разомкнутом состоянии она нейтральна, т.е. с течением времени не стремится к какому-то определенному положению (угол поворота оси двигателя остается произвольным при отсутствии напряжения на его входе).

Физический смысл критерия для простейших случаев (имеется ввиду т.н абсолютно устойчивые системы) совершенно очевиден: среди всех частот от ω=0 до ω =¥ не должно быть ни одной частоты w₀, которая при замыкании САР поступит на вход усиленной по амплитуде ( 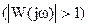и с фазовым сдвигом 180 градусов ( j₀(w)= p и точка -1+j0).

При 180-градусном сдвиге обратная связь на частоте w₀ превращается из отрицательной в положительную. Если к тому же модуль 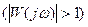, то создаются условия для возбуждении колебаний на этой частоте.

Достоинством критерия Найквиста заключается в том, что для определения устойчивости САР можно использовать экспериментально полученные амплитудно-фазовые характеристики. Это ценно в случае, когда ввиду сложности системы или ее звена получить соответствующее дифференциальное уравнение не представляется возможным.

Из критерия Найквиста следует метод логарифмических частотных характеристик, который в ряде случаев позволяет оценить устойчивость и САР, качество регулирования и синтезировать корректиреющие звенья почти без вычислительной работы.

В случае многоконтурной САР ее размыкание для получения передаточной функции разомкнутой системы может быть сделано в произвольном месте. Если, однако, с системе имеется один вход и один выход, то при размыкании системы на входе первого звена получим главную передаточную функцию разомкнутой системы, связывающую входной и выходной сигналы. Именно эта передаточная функция рассматривается при определении качества регулирования и при синтезе корректирующих звеньев.

Годограф устойчивой в замкнутом состоянии САР позволяет оценивать и качество регулирования по запасам устойчивости по фазе и по усилению.

Запасом устойчивости по амплитуде (усилению) - это расстояние между критической точкой (-1,j₀) и ближайшей к ней точкой пересечения годографа с отрицательной полуосью абсцисс. Для хорошо демпфированных систем этот запас более 6 дБ.

Запас устойчивости по фазе (m₀ ) - это угол между вектором W(jw_c) (w_c - частота среза, ½W(jω _с)½=1) и отрицательной полуосью абсцисс.

Его определяют как угол m₀=180-j₀(w_с) градусов. В хорошо демпфированных системах этот угол лежит в пределах 30-60 градусов. Если на частоте среза фазовый сдвиг меньше 180 градусов, то говорят об избытке фазы [5]. В соответствии с заданными запасами устойчивости можно определить запретную область, которую не должен пересекать годограф.

Для условно устойчивых САУ запас устойчивость по модулю определяется с двух сторон - запас при увеличении и запас при уменьшении усиления.