Свойства определённого интеграла.
1. 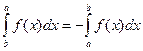 .
.
Это свойство часто бывает нужно при заменах переменной в определённом интеграле. Так, например, если замена 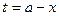 , то большему
, то большему 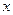 будет соответствовать меньшее
будет соответствовать меньшее 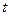 и наоборот. То есть, интеграл получится от большего числа до меньшего, и надо будет поменять пределы интегрирования обратно, и при этом сменится знак.
и наоборот. То есть, интеграл получится от большего числа до меньшего, и надо будет поменять пределы интегрирования обратно, и при этом сменится знак.
2. 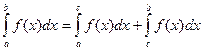 .
.
Кстати, свойство верно даже в том случае, если 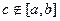 , тогда просто получится, что интегралы по
, тогда просто получится, что интегралы по 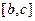 и
и 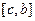 взаимоуничтожатся.
взаимоуничтожатся.
Следующие два свойства относятся к уже знакомому понятию «линейность»: можно вынести константу и интеграл от суммы функций разбить на сумму двух интегралов.
3. 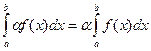 и 4.
и 4. 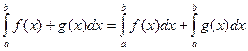 .
.
5. Если 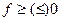 то
то 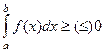 .
.
Действительно, если в интегральной сумме 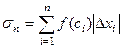 все числа
все числа 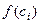 положительны (отрицательны) то и сумма положительна (отрицательна).
положительны (отрицательны) то и сумма положительна (отрицательна).
6. если 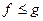 то
то 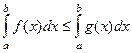 .
.
Свойство 6 следует из 5, ведь можно рассмотреть 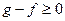 .
.
Свойство 7. 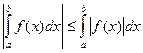
(Модуль интеграла меньше или равен, чем интеграл модуля).
Действительно, если сначала вычислить интеграл, то площади, расположенные выше и ниже оси, частично вычитаются, и число получается меньше. А если заранее взять модуль функции, то эти площади не вычитаются, а складываются:
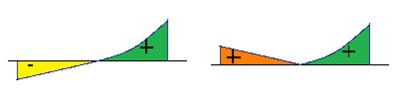
Равенство здесь возможно лишь в том случае, когда в области интегрирования функция нигде не меняет знак.
Свойство 8. Если 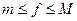 то
то 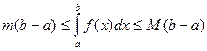 .
.
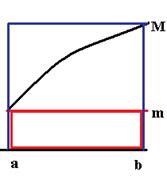
Площадь прямоугольника, соответствующего минимальной высоте графика функции, это и есть 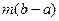 , что меньше, чем площадь криволинейной трапеции, а
, что меньше, чем площадь криволинейной трапеции, а 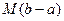 наоборот, больше, ведь это площадь прямоугольника, соответствущего максимальной высоте графика.
наоборот, больше, ведь это площадь прямоугольника, соответствущего максимальной высоте графика.
А теперь представьте себе, что высота прямоугольника плавно растёт от 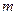 до
до 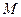 . Площадь при этом растёт от
. Площадь при этом растёт от 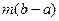 до значения
до значения 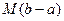 . Но ведь значение интеграла между этими числами, следовательно, при какой-то высоте
. Но ведь значение интеграла между этими числами, следовательно, при какой-то высоте 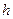 , площадь растущего прямоугольника сравняется со значением интеграла.
, площадь растущего прямоугольника сравняется со значением интеграла.
Свойство 9. Существует такое 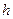 , где
, где 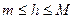 , что
, что 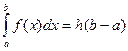 .
.
Свойство 10. Если f непрерывна, то существует точка 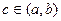 , такая, что:
, такая, что: 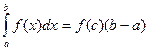 .
.
Отличие от прошлого свойства в том, что это среднее значение не просто существует, а ещё достигается в какой-то точке, то есть обязательно найдётся точка графика на этой высоте. Для разрывной могло быть и не так: например, если ступенчатая функция на одной половине отрезка навна 1, а на второй половине 2, то средняя высота графика 1,5 но ведь график нигде не проходит через эту высоту.
Основной формулой в теме «определённый интеграл» является формула Ньютона-Лейбница 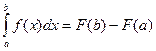 . Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.
. Она позволяет сразу же вычислить определённый интеграл, если известен неопределённый.
Но на самом деле, связь между этими двумя видами интегралов двусторонняя, т.е. и неопределённый интеграл может быть вычислен с помощью определённого. А именно, если рассматривать функцию 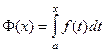 то есть определённый интеграл с переменным верхним пределом.
то есть определённый интеграл с переменным верхним пределом.
Теорема 1. Функция 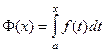 является первообразной от функции
является первообразной от функции 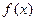 .
.
Доказательство. Нужно доказать, что 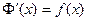 .
.
Рассмотрим подробнее производную функции 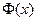 . По определению,
. По определению,
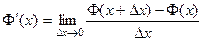 .
.
В данном случае, это 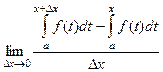 , по свойству 2, интеграл по отрезку
, по свойству 2, интеграл по отрезку 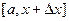 можно представить в виде суммы двух интегралов, а именно, по
можно представить в виде суммы двух интегралов, а именно, по 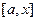 и
и 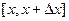 . Чертёж:
. Чертёж:
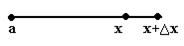
При этом интеграл по 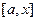 там в разности есть ещё и со знаком «минус», то есть он в итоге сокращается.
там в разности есть ещё и со знаком «минус», то есть он в итоге сокращается.
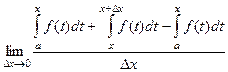 =
= 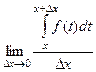 .
.
По свойству 10, интеграл по отрезку 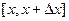 можно представить как некоторое среднее значение, т.е. в какой-то точке
можно представить как некоторое среднее значение, т.е. в какой-то точке 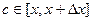 , умноженное на длину отрезка.
, умноженное на длину отрезка.
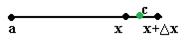
В общем случае длина была равна 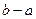 , а для данного отрезка это просто
, а для данного отрезка это просто 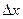 . Тогда:
. Тогда: 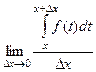 =
= 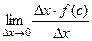 =
= 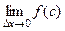 .
.
Однако точка 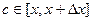 , поэтому при
, поэтому при 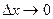 , точка
, точка 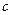 , которая находится где-то между
, которая находится где-то между 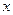 и
и 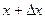 , стремится к левой границе отрезка:
, стремится к левой границе отрезка: 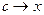 . Поэтому в итоге
. Поэтому в итоге 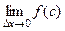 =
= 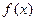 .
.
Теорема 2. (Ньютона-Лейбница). Если 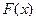 - какая-либо первообразная от
- какая-либо первообразная от 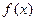 , то верна формула:
, то верна формула: 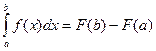 .
.
Доказательство. Если 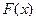 есть произвольная первообразная, то она отличается на какую-то константу
есть произвольная первообразная, то она отличается на какую-то константу 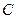 от той первообразной, которую мы рассматривали в теореме 1. То есть
от той первообразной, которую мы рассматривали в теореме 1. То есть 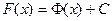 , что означает
, что означает
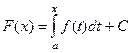 . Запишем это равенство в точке
. Запишем это равенство в точке 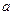 , получится
, получится 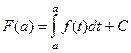 но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда
но ведь интеграл по одной точке это 0, там нулевая длина основания, а значит и нулевая площадь. Тогда 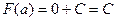 . вот, кстати, мы заодно и установили, как связана константа
. вот, кстати, мы заодно и установили, как связана константа 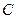 с выбором начальной точки
с выбором начальной точки 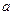 .
.
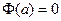 , а на сколько по высоте отличается от
, а на сколько по высоте отличается от 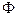 любая другая первообразная - это и есть значение
любая другая первообразная - это и есть значение 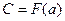 .
.
Итак, теперь ясно, что 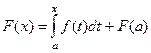 .
.
А теперь рассмотрим это выражение в точке 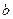 .
.
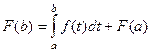 , то есть
, то есть 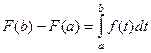 . Но ведь переменная
. Но ведь переменная 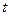 вводилась исключительно для того, чтобы отличать
вводилась исключительно для того, чтобы отличать 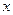 внутри функции и на верхнем пределе интеграла. Теперь, когда перешли к фиксированным границам в интеграле, можно сделать тривиальную замену
внутри функции и на верхнем пределе интеграла. Теперь, когда перешли к фиксированным границам в интеграле, можно сделать тривиальную замену 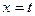 и запись примет вид
и запись примет вид 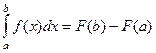 , что и требовалось доказать.
, что и требовалось доказать.
Примеры вычисления по формуле Ньютона-Лейбница.
Пример. Найти интеграл 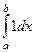 .
.
Решение. 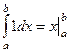 =
= 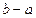 .
.
Пример. Найти интеграл 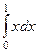 .
.
Решение. 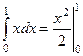 =
= 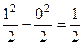 .
.
Пример. Найти интегралы 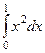 и
и 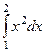 .
.
Решение. 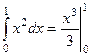 =
= 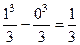 .
.
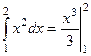 =
= 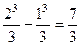 .
.
Пример. Найти интеграл 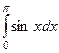 .
.
Решение. 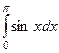 =
= 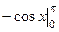 =
= 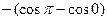 =
= 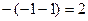 .
.
Пример. Найти интеграл 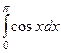 .
.
Решение. 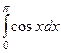 =
= 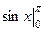 =
= 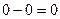 .
.
Вид формулы интегрирования по частям для определённого интеграла: 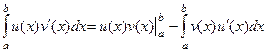 .
.
Особенности замены переменной в определённом интеграле (пересчёт пределов интегрирования, и можно не возвращаться к старой переменной, то есть не делать обратную замену).
Пример. Вычислить интеграл 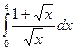
Решение. При замене 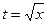 мы адаптируем границы к новой переменной, то есть, если
мы адаптируем границы к новой переменной, то есть, если 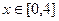 , то
, то 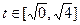 =
= 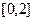 .
.
Тогда 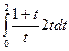 =
= 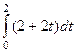 =
= 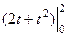 = 8.
= 8.
Конечно, старые границы могут остаться прежними, например, при такой замене 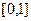 отобразится в
отобразится в 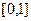 . Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
. Но, как правило, при замене верхний и нижний предел интегрирования тоже изменяются.
Замена в определённом интеграле должна задаваться взаимно-однозначной функцией 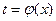 , то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например,
, то есть монотонной функцией. Иначе можно столкнуться с такими парадоксами: например, 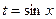 , интеграл от 0 до
, интеграл от 0 до 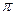 . Тогда по переменной
. Тогда по переменной 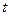 получаем интеграл по промежутку
получаем интеграл по промежутку 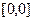 , и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной
, и он был бы в любом случае равен 0. Чтобы избежать такого противоречия, надо было бы разбить исходный интеграл по переменной 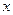 на 2 части, по
на 2 части, по 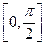 и
и 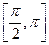 .
.
