Постановка задачи о различии средних для зависимых выборок
Существует много практических задач, в которых две сравниваемые выборки взаимосвязаны в силу особенностей организации эксперимента или просто потому, что этой взаимосвязи нельзя избежать.
Примеры зависимых выборок:
- первая и вторая выборки состоят из наблюдений типа «до – после»;
- первая выборка – совокупность значений времени самостоятельного выполнения задания, а вторая – совокупность значений времени выполнения задания под наблюдением и при руководстве преподавателя.
В практике психологических, педагогических, медицинских исследований часто используются так называемые парные сравнения. При парных сравнениях нельзя использовать методы для независимых выборок, поскольку это приведет к большим ошибкам.
Парные сравнения выгодно использовать, если удастся организовать эксперимент так, что будет устранено влияние мешающих факторов (эффект обучения, усталость и т.д.). При парных сравнениях нельзя использовать рассмотренные выше методы для независимых выборок, поскольку это приведет к большим ошибкам. Для сравнения средних значений здесь используется модификация 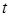 -критерия для связанных выборок. Особенность в том, что гипотеза формулируется в отношении разностей
-критерия для связанных выборок. Особенность в том, что гипотеза формулируется в отношении разностей 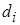 сопряженных пар наблюдений.
сопряженных пар наблюдений.
Для сравнения средних значений здесь используется модификация 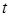 -критерия Стьюдента для зависимых выборок.
-критерия Стьюдента для зависимых выборок.
Постановка задачи.Даныдве зависимыевыборки объема 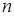 , то есть связанные пары наблюдений:
, то есть связанные пары наблюдений: 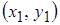 ,
, 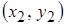 , …,
, …, 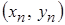 . Проверяется гипотеза
. Проверяется гипотеза 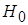 о равенстве математических ожиданий
о равенстве математических ожиданий  . Альтернативной гипотезой
. Альтернативной гипотезой 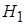 является гипотеза
является гипотеза  .
.
Условия применения 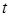 -критерия для зависимых выборок
-критерия для зависимых выборок
1. Измерение признака проведено в шкале интервалов и отношений.
2. Сравниваемые выборки случайно извлекаются из нормальных совокупностей с одинаковой дисперсией.
3. Предполагается, что разность связанных пар результатов измерения 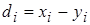 имеет нормальное распределение с параметрами
имеет нормальное распределение с параметрами 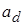 и
и 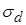 .
.
Критерий (правило) проверки гипотезы
1. Формулируем нулевую гипотезу 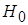 :
: 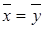 , что генеральные средние равны.
, что генеральные средние равны.
2. Формулируем альтернативную гипотезу 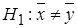 .
.
3. Назначаем уровень значимости 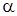 .
.
4. Делаем предположение о нормальном распределении разностей 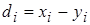 .
.
5. Вычисляется эмпирическое значение 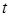 -критерия по формуле
-критерия по формуле
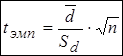 ,
,
где величины 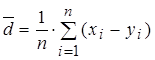 ;
; 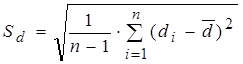 .
.
6. По таблице критических значений 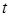 -критерия распределения Стьюдента находится критическое значение
-критерия распределения Стьюдента находится критическое значение 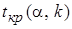 при уровне значимости
при уровне значимости 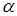 и числе степеней свободы
и числе степеней свободы 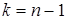 .
.
7. Сравниваем 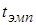 и
и 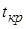 . Если
. Если  , то гипотеза
, то гипотеза 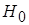 отклоняется, так как
отклоняется, так как 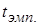 попало в критическую область. Значит, наблюдаемое различие между средними значениями двух связанных выборок значимо на уровне значимости
попало в критическую область. Значит, наблюдаемое различие между средними значениями двух связанных выборок значимо на уровне значимости 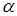 . Если
. Если 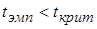 , то различие между средними значениями двух связанных выборок статистически незначимо.
, то различие между средними значениями двух связанных выборок статистически незначимо.
