Критерий (правило) проверки гипотезы
1. Проверяем нулевую гипотезу 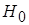 :
:  о равенстве генеральных средних (между средними значениями признака в выборках нет значимого различия).
о равенстве генеральных средних (между средними значениями признака в выборках нет значимого различия).
2. Формулируем альтернативную гипотезу 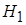 :
:  о неравенстве генеральных средних. В качестве
о неравенстве генеральных средних. В качестве 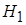 могут выступать и другие предположения:
могут выступать и другие предположения: 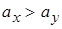 или
или 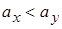 .
.
3. Назначаем уровень значимости 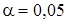 (или
(или  ).
).
4. Вычисляем выборочные средние значения 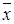 и
и  .
.
 ,
, 
5. Вычисляем выборочное значение 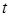 -критерия
-критерия 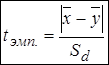 , где выражение для
, где выражение для  равно
равно  . Доказано, что статистика
. Доказано, что статистика 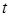 распределена по закону Стьюдента с
распределена по закону Стьюдента с 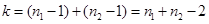 степенями свободы. Таблица критических точек распределения Стьюдента приведена в Приложении.
степенями свободы. Таблица критических точек распределения Стьюдента приведена в Приложении.
6. По таблице критических точек распределения Стьюдента находим критическое значение при  .
.
Альтернативная двусторонняя гипотеза 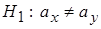 . Тогда на уровне значимости
. Тогда на уровне значимости 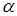 определяются по таблице две критические точки распределения Стьюдента:
определяются по таблице две критические точки распределения Стьюдента: 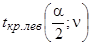 и
и  . Критическая область (отклонения гипотезы
. Критическая область (отклонения гипотезы 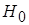 ) является двусторонней и распадается на два интервала:
) является двусторонней и распадается на два интервала:
 и
и 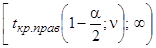 . (5.5)
. (5.5)
Вероятность 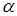 ошибочного отклонения нулевой гипотезы делится пополам между интервалами и при нахождении критических точек фигурирует
ошибочного отклонения нулевой гипотезы делится пополам между интервалами и при нахождении критических точек фигурирует  . Поскольку кривая распределения
. Поскольку кривая распределения 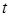 Стьюдента симметрична, то критические точки
Стьюдента симметрична, то критические точки  и
и 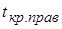 симметричны относительно начала координат, т.е.
симметричны относительно начала координат, т.е.  .
.
2) Альтернативная правосторонняя гипотеза 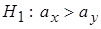 . Тогда на уровне значимости
. Тогда на уровне значимости 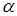 определяется по таблице граница правой критической области – критическая точка
определяется по таблице граница правой критической области – критическая точка  . Критическая правосторонняя область имеет вид
. Критическая правосторонняя область имеет вид
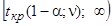 . (5.6)
. (5.6)
3) Альтернативная левосторонняя гипотеза 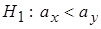 . Тогда на уровне значимости
. Тогда на уровне значимости 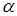 определяется по таблице граница левой критической области – критическая точка
определяется по таблице граница левой критической области – критическая точка  и область имеет вид
и область имеет вид
 .
.
7. Сравниваем 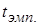 и
и 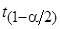 , т.е. определяем, принадлежит ли значение
, т.е. определяем, принадлежит ли значение  критической области.
критической области.
Если 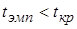 , т.е.
, т.е.  попало в область допустимых значений, то гипотеза
попало в область допустимых значений, то гипотеза 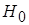 принимается. Говорят, что с ошибкой
принимается. Говорят, что с ошибкой 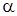 нет оснований для отклонения гипотезы
нет оснований для отклонения гипотезы 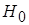 о незначимости различий между двумя генеральными средними. Различие между генеральными средними статистически незначимо (недостоверно) и объясняется случайными причинами, например, случайным отбором объектов выборки.
о незначимости различий между двумя генеральными средними. Различие между генеральными средними статистически незначимо (недостоверно) и объясняется случайными причинами, например, случайным отбором объектов выборки.
Если же  , то гипотеза
, то гипотеза 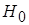 отклоняется, так как
отклоняется, так как 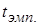 попало в критическую область. Отметим, что значение
попало в критическую область. Отметим, что значение 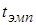 всегда положительно, поэтому достаточно сравнить его только с правой критической точкой
всегда положительно, поэтому достаточно сравнить его только с правой критической точкой 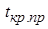 .
.
Таблица 5.1 – Принятие решения об оценке различия между средними значениями признака в двух выборках
| Вид альтернативной гипотезы | 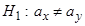 |  |  |
| Критическая область | Двусторонняя область  и и 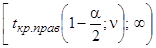 | Правосторонняя область 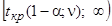 | Левосторонняя область  |
Условие попадания значения  в критическую область в критическую область |  или или 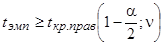 |  |  |
| Выводы | Нулевая гипотеза 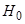 о незначимости различий между средними значениями признака отклоняется. На уровне значимости о незначимости различий между средними значениями признака отклоняется. На уровне значимости 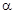 принимается альтернативная гипотеза принимается альтернативная гипотеза 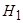 о значимости различий. Считается, что выборочные средние значения значимо различаются на уровне значимости о значимости различий. Считается, что выборочные средние значения значимо различаются на уровне значимости 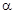 , и это различие объясняется тем, что сами генеральные средние различны. Выборки относятся к двум разным генеральным совокупностям и являются неоднородными. , и это различие объясняется тем, что сами генеральные средние различны. Выборки относятся к двум разным генеральным совокупностям и являются неоднородными. |
Если 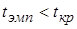 , т.е.
, т.е.  попало в область допустимых значений, то говорят, что с ошибкой
попало в область допустимых значений, то говорят, что с ошибкой 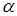 % нет оснований для отклонения гипотезы
% нет оснований для отклонения гипотезы 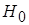 о незначимости различий между средними значениями признака. Различие между выборочными средними статистически незначимо (недостоверно) и объясняется случайными причинами, например, случайным отбором объектов выборки.
о незначимости различий между средними значениями признака. Различие между выборочными средними статистически незначимо (недостоверно) и объясняется случайными причинами, например, случайным отбором объектов выборки.
Отметим, что значение  всегда положительно, поэтому достаточно сравнить его только с правой критической точкой
всегда положительно, поэтому достаточно сравнить его только с правой критической точкой 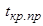 .
.
