Стохастические модели управления запасами с фиксированным временем задержки поставок

Усложним модель. В рассмотренных выше идеализированных моделях управления запасами предполагалось, что пополнение запаса происходит практически мгновенно. Однако, в ряде задач время задержки поставок может оказаться настолько значительным, что его необходимо учитывать в модели.

Пусть за время задержек поставок 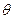уже заказана n партия по одной в каждый из периодов продолжительностью 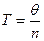. Введем обозначения:

s_н.з – первоначальный уровень запаса (к началу первого периода);

s_i – запас за i-ый период;

r_i – спрос за i-ый период;

q_i – пополнение запаса за i-ый период.

тогда к концу n-ого периода на склад поступит 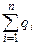единиц продукта, а будет израсходовано 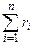единиц, т.е.

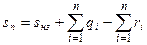(3.39)

или

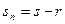(3.40)

где 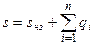(3.41)

а 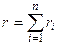(3.42)

Требуется найти оптимальный объем партии заказа, который необходимо сделать за последний n-ый период, предшествующий поступлению ранее сделанного заказа.

Математическое ожидание суммарных затрат в этом случае определяется по формуле (3.28)

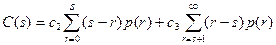, а оптимальный запас s находится по формуле

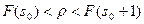(3.43)

Найдя оптимальный запас s₀ и зная q₁, q₂,…, q_n-1 можно вычислить q_n, т.е.

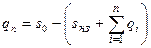(3.44)

Пример 9. Ежедневно заказываемый скоропортящийся товар поступает в магазин спустя 7 дней после заказа. В момент очередного заказа товар составил в стоимостном выражении 10 ден.ед. А данный товар в день изготовления приносит прибыль 0,95 ден.ед., а не проданный в этот день товар может быть реализован с убытком 0,10 ден.ед.

На основании опытных данных поучено следующее распределение спроса на данный товар:

r
p(r)	0,00	0,00	0,01	0,02	0,05	0,08	0,11	0,12	0,14	0,13	0,10
r											>200
p(r)	0,08	0,05	0,03	0,02	0,02	0,01	0,01	0,01	0,01	0,00	0,00

Необходимо определить оптимальный объем заказанного товара q₇ на седьмой день после заказа.

Решение: плотность убытков из-за дефицита товаров

;

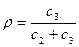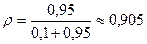
Учитывая условие 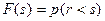, найдем значение функции распределения спроса

s	r	F(r)	s	r	F(r)	s	r	F(r)	s	r	F(r)
		0,00			0,16			0,76			0,96
		0,00			0,27			0,84			0,97
		0,01			0,39			0,89			0,98
		0,03			0,53			0,92			0,99
		0,08			0,66			0,94	>190	>190	1,00

Из таблицы определяем оптимальную партию s₀ по условию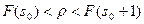

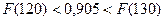
Таким образом, оптимальный запас товара за 7 дней должен быть на сумму 120 ден.ед., откуда оптимальный объем заказанного товара на седьмой день составит

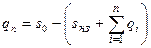
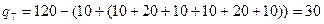ден.ед.

Замечание: Найти аналитически оптимальное значение точки запаса s₀ и объем партии n удается только в сравнительно простых случаях. Если же система хранения запасов имеет сложную структуру (много видов хранимой продукции, иерархическая система складов), в этом случае используемые стохастические модели сложны, а их параметры меняются во времени, то единственным средством анализа такой системы становится имитационное моделирование, позволяющее имитировать («проигрывать») на ЭВМ функционирование системы, исследуя ее поведение при различных условиях, значениях параметров, отражая их случайный характер, изменение во времени и т.п.

Основные понятия теории игр. Классификация игр. Формальное представление игр

При решении задач по теории оптимизации рассматривались такие задачи принятие решений, когда выбор решения осуществляется одним лицом. В подобных задачах рационального ведения хозяйства решение выбирается при предположении о том, что известны целевая функция, различные способы действия и ограничения. Рассмотрим задачи принятия решений в ситуациях с несколькими участниками, когда значение целевой функции для каждого из субъектов зависит от решений принимаемых всеми остальными участниками. Предметом теории игр являются такие ситуации, в которых важную роль играют конфликты и совместные действия.

Конфликт может возникнуть также из различия целей, которые отражают не только не совпадающие интересы различных сторон, но и многосторонние интересы одного и того же лица.

Всякая претендующая на адекватность математическая модель социально-экономического явления должна отражать присущие ему черты конфликта, т.е. описывать:

А) множество заинтересованных сторон (обычно их называют игроками, они еще именуются субъектами, лицами, сторонами, участниками). В случае если число игроков конечно, они различаются по своим номерам (1-й игрок, 2-й игрок и т.д.), или по присваемым им именам (например, Продавец и Покупатель в ситуации монополии – монопсонии);

Б) возможные действия каждый из сторон, именуемым также стратегиями или ходами;

В) интересы сторон, представленные функциями выигрыша (платежа) для каждого из игроков.

В теории игр предполагается, что функции выигрыша и множество стратегий, доступных каждому из игроков, общественны, т.е. каждый игрок знает свою функцию выигрыша и набор имеющихся в его распоряжении стратегий, а также функции выигрыша и стратегии всех остальных игроков, и в соответствии с этой информацией организует свое поведение.

Формализация содержательного описания конфликта представляет собой его математическую модель, которую называют игрой.

Классификация игр.

Различные виды игр можно классифицировать, основываясь на том или ином принципе:

- по числу игроков;

- по числу стратегий;

- по свойствам функций выигрыша;

- по возможностям предварительных переговоров;

- взаимодействия между игроками в ходе игры.

По числу игроков различают игры с двумя, тремя и более участниками. В принципе возможны так же игры с бесконечным числом игроков.

По количеству стратегий различают конечные и бесконечные игры. В конечных играх игроки располагают конечным числом возможных стратегий. Сами стратегии в конечных играх нередко называют чистыми стратегиями.

В бесконечных играх игроки имеют бесконечное число возможных стратегий, так в ситуации Продавец-Покупатель каждый из игроков может назвать любую цену и количество продаваемого (покупаемого) товара.

По свойствам функции выигрыша (платежных функций) – возможна ситуация, когда выигрыш одного из игроков равен проигрышу другого, т.е. на лицо конфликт между игроками. Подобные игры называются играми с нулевой суммой, или антагонистическими играми. Прямой противоположностью такого типа являются игры с постоянной разностью, в которых игроки и выигрывают, и проигрывают одновременно так, что им выгодно действовать сообща.

Между эти крайними случаями имеется множество игр с ненулевой суммой, где имеются и конфликты, и согласованные действия игроков.

В зависимости от возможности предварительных переговоров между игроками различают кооперативные и некооперативные игры.

Игра называется кооперативной, если до начала игры игроки образуют коалиции и принимают взаимообязывающие соглашения о своих стратегиях.

Игра, в которой игроки не могут координировать свои стратегии подобным образом, называется некооперативной. Очевидно, что все антагонистические игры могут служить примером некооперативных игр.

Формальное представление игр

Множество всех игроков, обозначаемое I, в случае их конечного числа может задаваться простым перечислением игроков. Например, I=(1,2) при игре в орлянку; I=(1,2,…,n) в случае анализа результатов голосования.

Множество стратегий игрока i обозначим через x_i. При игре в орлянку каждый игрок располагает двумя стратегиями: x_i=(орел, решка). Каждый участник голосования имеет выбор на множестве стратегий [За, Против].

Покупатель и продавец могут назначать некоторую неотрицательную цену на продаваемый (покупаемый) товар, т.е. множество стратегий каждого из них: x_i; p₀>0. В каждой партии игрок выбирает свою стратегию x_i, в результате чего оказывается набор стратегий x=(x₁, x₂,…, x_n), называемых ситуацией.

Ситуация в парламенте описывает список (за, за, против, за,…), полученный в итоге голосования.

Заинтересованность игроков в ситуациях проявляется в том, что каждому игроку i в каждой ситуации х приписывается число, выражающее степень удовлетворения его интересов в данной ситуации. Это число называется выигрышем игрока i и обозначается через h_i(x), а соответствие между набором ситуаций и выигрышем I называется функцией выигрыша (платежной функцией) этого игрока H_i.

В случаях конечной игры двух лиц функции выигрыша каждого из игроков удобно представить в виде матрицы выигрышей, где строки представляют стратегии одного игрока, столбцы – стратегии другого игрока, а в клетках матрицы указывают выигрыши каждого из игроков в каждой из образующихся ситуаций. (Данная форма представления конечных игр двух лиц объясняет общее для них название – матричные игры).

Например, в случае игры в орлянку каждый из игроков имеет по две стратегии Орел и Решка. Если оба игрока выбирают одинаковые стратегии, первый игрок выигрывает 1 рубль, а второй проигрывает рубль. В случае, когда оба игрока выбирают различные стратегии, первый игрок проигрывает один рубль, второй выигрывает один рубль.

Матрица выигрышей первого игрока

Стратегии первого игрока		Стратегии второго игрока
	Орел	Решка	H1
Орел		-1
Решка	-1

Матрица выигрышей второго игрока

Стратегии первого игрока		Стратегии второго игрока
	Орел	Решка	H2
Орел	-1
Решка		-1

Для антагонистических игр выполняется соотношение H₁=-H₂

Для наглядности обе матрицы совмещают в одну:

Стратегии первого игрока		Стратегии второго игрока
	Орел	Решка
Орел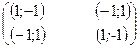
Решка

Рассмотрим пример записи функции для бесконечной игры. Для случая двух игроков, каждый из игроков может объявить цену p_i, по которой он хотел бы продать некоторое количество товара. При этом предполагается, что потребители приобретают товар у фирмы, объявившей меньшую цену, или распределят свой спрос между фирмами в случае, если они назначили одинаковую цену.

Если функцию спроса в зависимости от цены на товар обозначить – d(p), то функция выигрыша первой фирмы П₁(p₁,p₂) будет выглядеть: