Статистическая детерминированная модель с дефицитом

В рассматриваемой модели предполагаем наличие дефицита. Это означает, что при отсутствии запасаемого продукта, т.е. при y(t)=0 спрос сохраняется с той же интенсивностью r(t)=b, но потребление запаса отсутствует – b(t)=0, вследствие чего накапливается (формируется) дефицит со скоростью b. График изображен ниже.

Убывание графика ниже оси абсцисс в области отрицательных значений, в отличие от предыдущего графика, характеризует накопление дефицита.

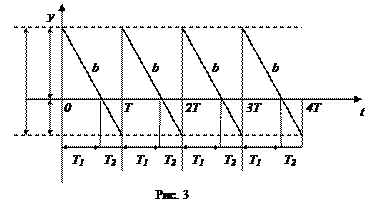
Из приведенного рисунка следует, что каждый период «пилы» 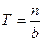разбиваются на два временных интервала, т.е. T=T₁+T₂, где T₁ – время, в течение которого производится потребление запаса, T₂ – время, когда отсутствует запас и накапливается дефицит, который будет перекрыт в момент поступления следующей партии.

Необходимость покрытия дефицита приводит к тому, что максимальный уровень запаса s в момент поступления каждой партии теперь равен ее объему n, а меньше его на величину дефицита n-s , накопившегося за время T₂.

Из геометрических соображений можно установить, что:

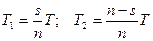(3.17)

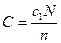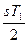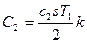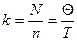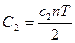В данной модели функцию суммарных затрат С наряду с затратами С₁ (на пополнение запаса) и С₂ (на хранение запаса) необходимо ввести затраты С₃ – штраф из-за дефицита, т.е. С=С₁+С₂+С₃. Затраты С₁ определяем как и в предыдущей модели . Затраты С₂ при линейном расходе запаса равны затратам на хранение среднего запаса, который за время потребления T₁ равен , поэтому , учитывая, что и получим:

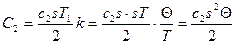(3.18)

При расчете затрат С₃ будем считать, что штраф за дефицит составляет в единицу времени С₃ на каждую единицу продукта.

Средний уровень дефицита за период Т₂ равен 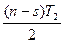, тогда штраф за этот период Т₂ составит 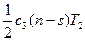, а за весь период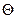

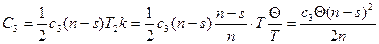(3.19)

Таким образом, суммарные затраты определяются:

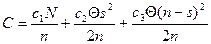(3.20)

Замечание: если n=s, то полученная формула сводится к ранее полученной в модели без дефицита.

Задача управления запасами сводится к отысканию такого объема партии n и максимального уровня запаса s, при котором функция (3.20) принимает минимальное значение. Другими словами, необходимо исследовать функцию двух переменных C(n,s) на экстремум. Для этого приравняем частично производные 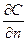и 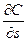к нулю, получим систему уравнений

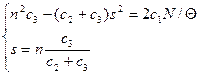(3.21)

Решая эту систему получим выражения для наиболее экономичного объема партии 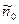и максимального уровня запаса 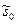для модели с дефицитом

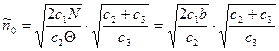(3.21)

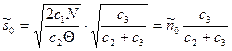(3.22)

Введем величину 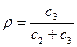(3.24) – она называется плотностью убытков из-за неудовлетворенного спроса 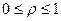. Если значение С₃ значительно превосходит С₂, то величина 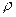близка к единице, если С₃ мало по сравнению с С₂, 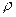близка к нулю. Выражения для 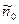и 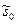можно записать с учетом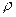

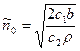(3.25)

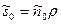(3.26)

Необходимо учитывать, что в силу 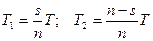; ; 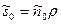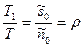и .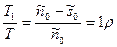

Поэтому утверждение о том, что плотность убытков из-за неудовлетворенного спроса равна 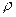, означает, что в течение 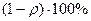времени от полного периода Т запас продукта будет отсутствовать.

Из сравнения 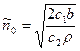и 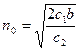следует, что оптимальный объем партий для модели с дефицитом и без дефицита при одинаковых параметрах связаны отношением:

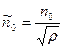(3.27)

Таким образом, оптимальный объем в модели с дефицитом всегда больше (в 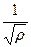), чем в модели без дефицита.

Пример 5. найти наиболее экономичный объем партии интервал между поставками, сохраняя условия примера 2, кроме недопустимости дефицита, если известно, что отсутствие на сборке каждой детали приносит в сутки убытки в размере 3,5 ден.ед.

Решение. По условию задачи с₃=3,5 ден.ед. в предыдущем примере было получено n₀=4335 и Т₀=13,2. Определим плотность убытков из-за неудовлетворенного спроса по формуле: 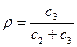; 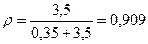, т.е. 100(1-0,909)=9,1% времени между поставками детали на сборке будут отсутствовать.

Оптимальный размер партии ;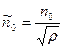

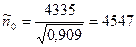
Пропорционально увеличению 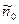должны увеличиться интервал между поставками, т.е.

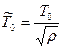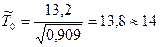; дней