Временные параметры сетевых графиков

Элемент сети, характеризующийся параметром	Наименование параметра	Условное обозначение параметра
Событие i	Ранний срок свершения события	tр(i)
Поздний срок свершения события	tп(i)
Резерв времени события	R(i)
Работа	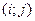Продолжительность работы	t(i,j)
Ранний срок начала работы	tрн(i,j)
Ранний срок окончания работы	tро(i,j)
Поздний срок начала работы	tпн(i,j)
Поздний срок окончания работы	tпо(i,j)
Полный резерв времени работы	Rп(i,j)
Частный резерв времени первого вида	R1(i,j)
Частный резерв времени второго вида или свободный резерв времени	Rс(i,j)
Независимый резерв времени	Rн(i,j)
Путь L	Продолжительность пути	t(L)
Продолжительность критического пути	tкр
Резерв времени пути	R(L)

1. Ранний (или ожидаемый) срок совершения i-го события t_р(i) определяется продолжительностью максимального пути предшествующему этому событию:

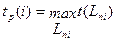
Для расчета раннего срока j-го события используют формулу:

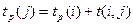
Если событие j имеет несколько предшествующих событий, то ранний срок события определяют по формуле:

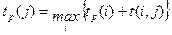
2. Поздний допустимый срок t_п(i) наступления события – это максимальный срок, который не нарушает поздних допустимых сроков наступления следующих за ним событий.

Поздний допустимый срок события 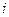равен разности между критическим временем проекта t_кр и максимальной длиной пути из i-го события в n – это время необходимое для выполнения всех работ, происходящих после наступления события.

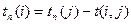– если из события выходит одна стрелка

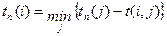– если из события выходит несколько стрелок

Расчет ранних и поздних сроков событий дает еще один способ нахождения критического пути, у работ лежащих на критическом пути совпадают ранние и поздние сроки событий t_р(i)= t_п(i).

Совпадение ранних и поздних сроков событий для определения критического пути является условием необходимым, но не достаточным (это условие не дает однозначного определения критического пути).

Любая задержка работ, лежащих не на критическом пути, нарушает сроки выполнения всего комплекса работ. Работы, не лежащие на критическом пути, допускают определенную задержку во времени выполнения, которая не сказывается на сроках выполнения всего комплекса работ.

Можно определить четыре вида резерва времени выполнения работы (i,j).

Полный резерв времени R_п(i,j) работы (i,j) – показывает на сколько можно увеличить время выполнения данной работы при условии, что срок выполнения комплекса работ не изменится. Полный резерв времени определяется по формуле:

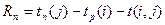
Этим резервом времени можно располагать при выполнении данной работы, если ее начальное событие свершится в ранний срок, и можно допустить свершение конечного события в его самый поздний срок.

Частный резерв времени первого вида R₁ – гарантийный резерв, это часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом позднего срока ее начального события.

Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершаться в свой самый поздние сроки

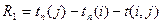
Частный резерв времени второго вида R_с(i,j) – свободный резерв времени, представляет собой часть полного резерва времени, на которую можно увеличить продолжительность работы, не изменив при этом раннего срока ее конечного события

Этим резервом можно располагать при выполнении данной работы в предположении, что ее начальное и конечное события свершаться в свои самые ранние сроки:

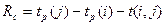
При использовании свободного резерва времени не расходуется резерв времени, следующих за ним работ.

Независимый резерв времени R_н(i,j) – часть полного резерва времени, получаемая для случая, когда все предшествующие работы заканчиваются в поздние сроки, а все последующие работы начинаются в ранние сроки:

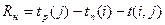
Использование независимого резерва времени не влияет на величину резервов времени других работ.

Работы, лежащие на критическом пути, так же как и критические событии, резервов времени не имеют.

Замечание: если какой-либо резерв времени оказывается отрицательным, то его приравнивают к нулю.

8.5. Сетевое планирование в условиях неопределенности

При определении временных параметров сетевого графика мы исходим из предположения, что время выполнения каждой работы точно известно.

Однако на практике система СПУ обычно применяется для планирования сложных разработок, не имевших в прошлом никаких аналогов.

Чаще всего продолжительность работ по сетевому графику заранее не известна и может принимать лишь одно из ряда возможных значений. Другими словами, продолжительность работы (i,j) является случайной величиной, характеризующейся своим законом распределения, а значит, и своими числовыми характеристиками – математическим ожиданием, средним значением 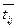и дисперсией .

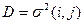Практически во всех системах СПУ принимается допущение, что распределение продолжительности работ обладает тремя свойствами:

- непрерывностью;

- унимодельностью, т.е. наличие единственного максимума у кривой распределения;

- двумя точками пересечения кривой распределения с осью Ох, имеющими неотрицательные абсциссы.

Кроме того, принимается, что распределение продолжительности работ обладает положительной асимметрией, т.е. максимум кривой смещен влево относительно медианы (линии, делящей площадь под кривой на две равные части). Распределение, как правило, более круто поднимается при удалении от минимального значения t и полного опускается при приближении к максимальному значению t.

Простейшим распределением с подобными свойствами является известное в математической статистике 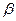-распределение. Анализ большого количества статистических данных (хронометража времени реализации отдельных работ, нормативные данные и т.п.) показывает, что 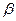-распределение можно использовать в качестве распределения продолжительности работ.

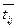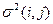Для определения числовых характеристик и данного распределения для работы (i,j) на основании опроса ответственных исполнителей проекта и экспертов определяют три временные оценки:

- t₀(i,j) – оптимистическую оценку, т.е. продолжительности работы (i,j) при самых благоприятных условиях;

- t_п(i,j) – пессимистическую оценку, т.е. продолжительности работы (i,j) при самых неблагоприятных условиях;

- t_нв(i,j) – наиболее вероятную оценку продолжительности работы (i,j) при нормальных условиях.

Предположение о 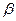-распределении продолжительности работы (i,j) позволяет получить оценки ее числовых величин:

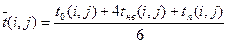
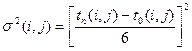
Обычно, оценить наиболее вероятное время выполнения работы t_нв(i,j) довольно сложно, поэтому реально на практике используют упрощенную (менее точную) оценку средней продолжительности работы 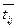на основании лишь двух задаваемых временных оценок t₀(i,j) и t_п(i,j):

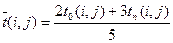
Зная 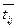и 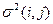можно определить временные параметры сетевого графика и оценить их надежность

При достаточно большом количестве работ, принадлежащих пути L, и выполнении некоторых весьма общих условий можно применить центральную теорему Ляпунова, на основании которой можно утверждать, что общая продолжительность пути L имеет нормальный закон распределения со средним значением 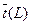, равное сумме средних значений продолжительности составляющих его работ 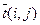и дисперсией 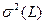, равный сумме соответствующих дисперсий :

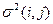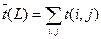
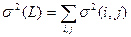
Сетевой график, в этом случае, представляет сеть не с детерминированными (фиксированными), а со случайными продолжительностями работ, и цифры над работами-стрелками указывают среднее значение 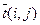продолжительности соответствующих операций, вычисленное по одной из приведенных выше формул, и известны все дисперсии .

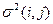Следует отметить, что и в этом случае временные параметры сетевого графика:

- длина критического пути t_кр;

- ранние и поздние сроки свершения событий ;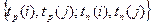

- резервы времени событий и работ определяются так же, как рассматривалось выше.

Но при этом необходимо учитывать, что эти параметры теперь будут являться средними значениями соответствующих случайных величин:

- средней длиной критического пути ;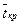

- средним значением данного срока наступления события ;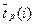

- средним значением полного резерва времени работы 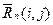и т.д.

Так, 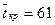, будет означать, что длина критического пути лишь в среднем составляет – 61 сутки, а в каждом конкретном случае возможны заметные отклонения от среднего значения (причем, чем больше суммарная дисперсия продолжительности работ критического пути, тем более вероятны значительные по абсолютной величине отклонения).

Поэтому предварительный анализ сетей со случайными продолжительностями работ, как правило, не ограничивается расчетами временных параметров сети.

В этом случае необходимо оценить вероятность того, что срок выполнения проекта t_кр не превзойдет заданного директивного срока T.

Полагая t_кр случайной величиной, имеющий нормальный закон распределения, получим:

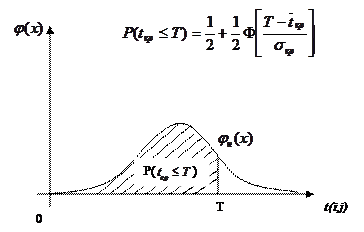
Численно эта вероятность равна площади заштрихованной фигуры, где 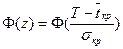– значение интеграла вероятностей Лапласа, 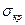– среднее квадратическое отклонение длины критического пути .

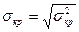t_кр и 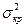определяются по формулам:

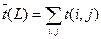
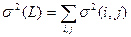
Если 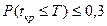(мало), опасность срыва заданного срока выполнения комплекса работ велика, необходимо принятие дополнительных мер (перераспределение ресурсов по сети, пересмотр состава работ, событий и т.п.).

Если 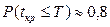, то очевидно с достаточной степенью надежности можно прогнозировать выполнение проекта в установленный срок.

В некоторых случаях возможно решение обратной задачи: определение максимального срока выполнения проекта с заданной надежностью (вероятностью) 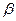. В этом случае:

,

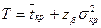где 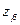– нормированное отклонение случайной величины, определяемое с помощью функции Лапласа .

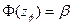Замечание:

1. На основании теоремы Ляпунова вывод о нормированном законе распределения случайной величины 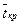правомерен лишь для достаточно большого числа критических работ(отсюда низкая точность ).

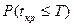2. Приведенный метод расчета имеет принципиальный недостаток оценки параметров сложных сетей с большим количеством работ. Это можно объяснить тем, что на практике нередки случаи, когда дисперсии 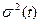длин некритических (но близкие к критическому) существенно больше, чем 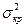. Поэтому при изменении ряда условий в данном конкретном комплексе работ возможен переход к новым критическим путям, которые в расчете не учитываются.

3. Различия между событием с детерминированными случайными продолжительностями работ не следует путать с различием детерминированных и стохастических сетей. Последнее различие связано со структурой самой сети.

Рассмотренные выше сети являлись детерминированными. Работы в них могли характеризоваться не только детерминированными, но и случайными продолжительностями.

Однако встречаются проекты, когда на некоторых этапах тот или иной комплекс последующих работ зависит от неизвестного заранее результата. Какой из этих комплексов работ будет фактически выполняться, заранее неизвестно, и может быть предсказано с некоторой вероятностью.

Например: может быть предусмотрено несколько вариантов продолжения исследования в зависимости от полученных опытных данных или несколько вариантов строительства предприятий различной мощности по обработке сырья в зависимости от результатов разведки запасов этого сырья. Такие сети называются стохастическими.

В свою очередь, стохастические сети так же, как и детерминированные, могут характеризоваться детерминированными либо случайными продолжительностями.